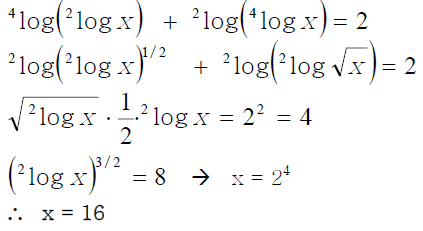Blog Koma - Hallow sahabat koma, bagaimana kabarnya hari ini? Semoga baik-baik saja ya.
Pada artikel ini kita akan membahas
Solusi OSP Matematika SMA Tahun 2003 sebagai pendukung dan menambah wawasan pemahaman
berbagai variasi soal-soal olimpiade matematika tingkat SMA. Dengan berlatih secara rutin dan giat dalam mempelajari
Solusi OSP Matematika SMA Tahun 2003 yang ada, tentu sahabat koma akan lebih siap dalam menghadapi olimpiade atau kompetisi
matematika yang ada. Semangat terus untuk berlatih. Jika ada masukan atau ide atau cara lain mengenai
Solusi OSP Matematika SMA Tahun 2003 ini, mohon untuk dishare ke admin ya, biar terus ada perbaikan dan peningkatan
dari isi artikel yang ada di blog koma.

Soal-soal dengan Solusi Singkat
Soal Bagian I: Soal Isian Singkat
1). Jika
a dan
b bilangan bulat ganjil dengan
a>b, berapa
banyakkah bilangan bulat genap di antara
a dan
b?
2). Agung mendapatkan bahwa nilai rata-rata dari tiga ulangan matematika
yang diikutinya adalah 81. Nilai ulangan pertama adalah 85. Nilai
ulangan ketiga lebih rendah 4 dari nilai ulangan kedua. Berapakah nilai
ulangan kedua Agung?
3). Apakah himpunan jawab dari persamaan
|x+2|+|3x|=14?
4). Keempat bilangan 3, 5, 7, dan 8 akan diisikan ke dalam kotak-kotak
di bawah. Berapakah hasil terbesar yang dapat diperoleh?

5). Misalkan
x,
y,
z tiga bilangan asli berbeda. faktor persekutuan terbesar
ketiganya adalah 12, sedangkan kelipatan persekutuan terkecil ketiganya adalah 840.
Berapakah nilai terbesar bagi
x+y+z?
6). Berapakah bilangan bulat positif
k terkecil sehingga
20032003...2003⏟2003kkali habis dibagi 9?
7). Persamaan kuadrat
2x2−2(2a+1)x+a(a−1)=0 mempunyai dua akar real
x1 dan
x2. Berapakah nilai
a yang memenuhi persamaan kuadrat tersebut sehingga
x1<a<x2?
8). Dalam sebuah segitiga ABC siku-siku sama kaki, dibuat persegi PQRS sebagai
berikut: Titik P pada sisi AB, titik Q pada sisi AC, sedangkan titik-titik R dan S
pada sisi miring BC. Jika luas segitiga ABC adalah
x, berapakah luas persegi PQRS?
9). Upik melemparkan
n dadu. Ia menghitung peluang terjadinya jumlah mata dadu sama
dengan 6. Untuk
n berapakah peluang tersebut paling besar?
10). Suatu garis vertikal membagi segitiga dengean titik sudut
(0,0),
(1,1), dan
(9,1) menjadi dua daerah dengan luas yang sama. Apakah
persamaan garis tersebut?
11). Misalkan
m dan
n dua bilangan asli yang memenuhi
m2−2003=n2. Berapakah
mn?
12). Berapakah nilai
x yang memenuhi
4log(2logx)+2log(4logx)=2?
13). Titik P terletak di dalam persegi ABCD sedemikian rupa sehingga
AP:PB:CP=1:2:3. Berapakah besar sudut APB?
14). Dengan mengkombinasikan ketiga warna dasar merah, kuning, dan biru dapat dibentuk
warna-warna yang lain. Misalkan terdapat 5 kaleng cat warna merah, 5 kaleng warna
kuning, dan 5 kaleng warna biru. Budi boleh memilih kaleng manapun untuk mencampurkan
warna, dan semua cat dalam sebuah kaleng harus dipakai semua. Ada berapa pilihan warna
yang dihasilkan?
15). Pak Oto membeli dua mobil untuk dijual kembali. Ia memperoleh keuntungan 30% dari
mobil pertama, tetapi menderita kerugian 20% pada mobil kedua. Harga jual kedua mobil
sama. Berapa persenkah keuntungan (atau kerugian) pak Oto secara keseluruhan?
[Catatan: Semua persentase terhadap harga pembelian. Untuk jawaban, gunakan
tanda "
−" untuk menyatakan kerugian dan tanda "
+" untuk menyatakan keuntungan]
16). Empat pasang suami isteri menonton pagelaran orkestra. Tempat duduk mereka harus
dipisah antara kelompok suami dan kelompok isteri. Untuk masing-masing kelompok
disediakan 4 buah tempat duduk bersebelahan dalam satu barisan. Ada berapa banyak
cara memberikan tempat duduk kepada mereka?
17). Sebuah bola dengan jari-jari
r ditendang dari B ke A. Bola tersebut
menggelinding sebanyak tepat 10 putaran sebelum membentur bidang miring dan berhenti.
Berapakah jarak dari B ke A?

18). Berapakah sisa pembagian
1.1!+2.2!+3.3!+...+99.99!+100.100! oleh 101?
19). Suatu lingkaran mempunyai diameter AB yang panjangnya merupakan bilangan
bulat 2-angka. Tali busur CD tegak lurus pada AB dan memotong AB di titik H. Panjang
CD sama dengan bilangan yang diperoleh dengan menukar letak kedua angka dari panjang
AB. Jika jarak dari H ke pusat lingkaran merupakan bilangan rasional, berapakah
panjang AB?
20). Berapakah banyaknya cara memilih tiga bilangan berbeda sehingga tidak ada dua
bilangan yang berurutan, jika bilangan-bilangan tersebut dipilih dari
himpunan
{1,2,3,...,9,10} ?
Soal Bagian II: Soal Uraian
1). Andi, Beni, Coki, Doni dan Edo bermain kancil-serigala. Setiap anak menjadi
kancil atau serigala, tetapi tidak kedua-duanya. Kancil selalu jujur, sementara
serigala selalu berdusta. Andi berkata bahwa Beni adalah kancil. Coki berkata bahwa
Doni adalah serigala. Edo berkata Andi bukan serigala. Beni berkata Coki bukan kancil.
Doni berkata bahwa Edo dan Andi adalah binatang yang berbeda.
Tentukan banyaknya serigala dalam permainan ini.
2). Tentukan semua bilangan bulat
a dan
b sehingga bilangan
√2+√a√3+√b merupakan bilangan rasional.
3). Titik-titik P dan Q berturut-turut adalah titik tengah rusuk AE dan CG pada kubus
ABCD.EFGH. Jika panjang rusuk kubus adalah 1 satuan, tentukan luas segi-empat DPFQ?
4). Buktikan bahwa
999!<500999.
[catatan:
n!=1.2.3.4...n.]
5). Tiga buah titik terletak pada daerah yang dibatasi oleh sumbu
Y dan grafik
persamaan
7x−3y2+21=0. Buktikan bahwa sedkitnya dua di antara ketiga titik
tersebut mempunyai jarak tidak lebih dari 4 satuan.
Kembali ke
Daftar Isi Olimpiade Matik SMA
Kembali ke
Solusi Singkat Olim Matik SD-SMP-SMA
Demikian artikel
Solusi OSP Matematika SMA Tahun 2003 ini.
Silahkan juga baca materi lain yang berkaitan dengan materi ini. Setiap artikel akan diupdate secara bertahap. Terimakasih.