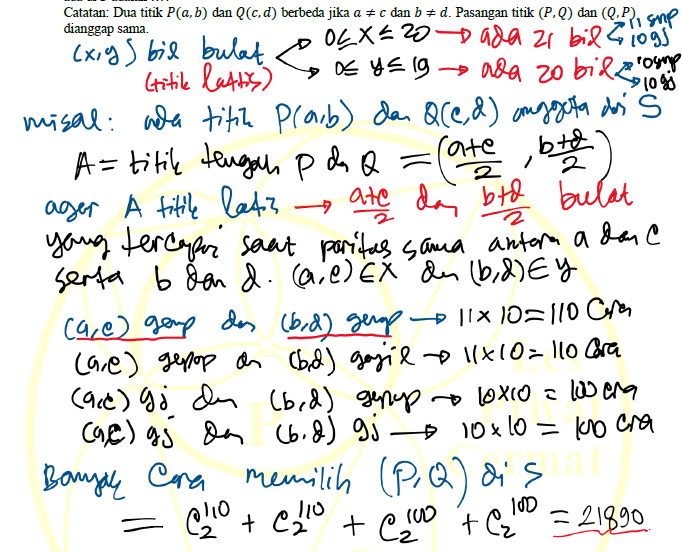Blog Koma - Hallow sahabat koma, bagaimana kabarnya hari ini? Semoga baik-baik saja ya.
Pada artikel ini kita akan membahas Solusi OSK Matematika SMA Tahun 2020 sebagai pendukung dan menambah wawasan pemahaman
berbagai variasi soal-soal olimpiade matematika tingkat SMA khususnya soal-soal OSN-K. Dengan berlatih secara rutin dan giat dalam mempelajari
Soal dan Solusi OSK Matematika SMA Tahun 2020 yang ada, tentu sahabat koma akan lebih siap dalam menghadapi olimpiade atau kompetisi
matematika yang ada. Semangat terus untuk berlatih. Jika ada masukan atau ide atau cara lain mengenai
Solusi OSK Matematika SMA Tahun 2020 ini, mohon untuk dishare ke admin ya, biar terus ada perbaikan dan peningkatan
dari isi artikel yang ada di blog koma.
Soal-soal dengan Solusi Singkat
1). Misalkan
$\, \, \, \, \, f(x)= \frac{3(x-1)(x-2)}{2} + \frac{(x-2)(x-3)}{2} - 2(x-1)(x-3)$.
Nilai dari $f(20)$ adalah ...?
Jika $AB = 1$, $BD = \sqrt{7}$ dan $AD = CD$, maka luas trapesium
tersebut adalah ...?
4). Misalkan $x$, $y$ bilangan asli sehingga $2x+3y = 2020$. Nilai
terbesar yang mungkin dari $3x+2y$ adalah ...?
5). Suatu barsan bilangan real $a_1, \, a_2, \, a_3, \, ...$
memenuhi $a_1 = 1$, $a_2 = \frac{3}{5}$, dan
$\, \, \, \, \, \, \frac{1}{a_n} = \frac{2}{a_{n-1}} - \frac{1}{a_{n-2}}$ untuk setiap $n \geq 3$.
Bilangan $a_{2020}$ dapat ditulis sebagai $\frac{p}{q}$ dengan $p$ dan $q$ bilangan asli relatif prima. Nilai $p+q$ adalah ...?
6). Diketahui $S$ adalah himpunan semua titik $(x, \, y)$ pada bidang
Cartesius, dengan $x$, $y$ bilangan bulat, $0 \leq x \leq 20$ dan
$0 \leq y \leq 19$. Banyaknya cara memilih dua titik berbeda di $S$
sehingga titik tengahnya juga ada di $S$ adalah ...?
Catatan: Dua titik $P(a, \, b)$ dan $Q(c, \, d)$ berbeda jika $a \neq c$ dan $b \neq d$. Pasangan titik $(P, \, Q)$ dan $(Q, \, P)$ dianggap sama.
7). Diketahui segitiga ABC dengan panjang sisi BC = 3, CA = 4, dan
AB = 5. Titik P terletak pada AB dan Q terletak pada AC sehingga
AP = AQ dan garis PQ membagi segitiga ABC menjadi dua daerah dengan
luas yang sama. Panjang segmen PQ adalah ...?
8). Himpunan penyelesaian dari persamaan
$|x+1|+ \left| \frac{19}{x-1} \right| = \frac{20-x^2}{1-x}$
adalah interval $[a, \, b)$.
Nilai dari $b-a$ adalah ...?
9). Misalkan $n \geq 2$ bilangan asli sedemikian sehingga untuk setiap
bilangan asli $a$, $b$ dengan $a+b = n$ berlaku $a^2+b^2$ merupakan
bilangan prima. Hasil penjumlahan semua bilangan asli $n$ semacam itu
adalah ...?
10). Suatu komite yang terdiri dari beberapa anggota hendap menghadiri
40 rapat. Diketahui bahwa setiap rapat dihadiri tepat 10 anggota komite
dan setiap dua anggota menghadiri rapat bersama paling banyak satu kali.
Banyaknya anggota komite terkeci yang mungkin adalah ...?
11). Diberikan segitiga ABC dengan $\angle ACB = 48^o$. Garis bagi
$\angle BAC$ memotong sisi BC dan lingkaran luar ABC berturut-turut di
titik D dan E. Jika $AC = AB + DE$, maka $\angle ABC = ...?$
12). Misalkan $p$ suatu bilangan prima sehingga terdapat pasangan
bilangan asli $(m, \, n)$ dengan $n > 1$ yang memenuhi
$mn^2 + mnp + m + n + p = mn + mp + np + n^2 + 2020$. Semua nilai $p$
yang mungkin adalah ...?
13). Misalkan $P(x)$ suatu polinom sehingga $P(x)+8x = P(x-2)+6x^2$.
Jika $P(1) = 1$, maka $P(2) = ... ?$
14). Banyaknya tripel bilangan bulat $(x, \, y, \, z)$ dengan
$0 \leq x \leq y \leq z$ yang memenuhi persamaan $x+y+z=32$ adalah ...?
15). Misalkan ABC segitiga dan P, Q, R titik pada sisi BC, CA, AB. Jika
luas segitiga ABC sama dengan 20 kali luas segitiga PQR dan
$\frac{AQ}{AC} + \frac{BR}{BA} + \frac{CP}{CB} = 1$, maka
$\left( \frac{AQ}{AC} \right) ^2 +
\left( \frac{BR}{BA} \right) ^2 +
\left( \frac{CP}{CB} \right) ^2 = ... ?$
16). Kwartet bilangan asli $(a, \, b, \, c, \, d)$ dikatakan keren jika
memenuhi $b = a^2 + 1$, $x = b^2 + 1$, $d = c^2 + 1$ dan
$\tau (a) + \tau (b) + \tau (c) + \tau (d)$ bilangan ganjil. Banyaknya
kwartet keren $(a, \, b, \, c, \, d)$ dengan $a, \, b, \, c, \, d < 10^6$
adalah ...?
Catatan: Untuk bilangan asli $k$, $\tau (k)$ menyatakan banyak faktor positif dari $k$.
17). Misalkan $a$, $b$, $c$ bilangan real tak negatif dengan $a+2b+3c = 1$.
Nilai maksimum dari $ab + 2ac$ adalah ...?
18). Bilangan asli $n$ terkecil sehingga $n+3$ dan $2020n + 1$ bilangan
kuadrat sempurna adalah ...?
19). Lima tim bertanding satu sama lain dimana setiap dua tim bertanding
tepat sekali. Dalam setiap pertandingan, masing-masing tim memiliki
peluang $\frac{1}{2}$ untuk menang dan tidak ada pertandingan yang
berakhir seri. Peluang bahwa setiap tim menang minimal sekali dan kalah
minimal sekali adalah ...?
20). Misalkan H adalah titik tinggi dari segitiga lancip ABC dan P
adalah titik tengah CH. Jika AP = 3, BP = 2 dan CP = 1, maka panjang
sisi AB adalah ...?
Catatan: Titik tinggi suatu segitiga adalah perpotongan ketiga garis tinggi dari segitiga tersebut.
Kembali ke Daftar Isi Olimpiade Matik SMA
Kembali ke Solusi Singkat Olim Matik SD-SMP-SMA
Demikian artikel Solusi OSK Matematika SMA Tahun 2020 ini. Silahkan juga baca materi lain yang berkaitan dengan materi ini. Setiap artikel akan diupdate secara bertahap. Semoga bermanfaat. Terimakasih.
$\, \, \, \, \, \, \frac{1}{a_n} = \frac{2}{a_{n-1}} - \frac{1}{a_{n-2}}$ untuk setiap $n \geq 3$.
Bilangan $a_{2020}$ dapat ditulis sebagai $\frac{p}{q}$ dengan $p$ dan $q$ bilangan asli relatif prima. Nilai $p+q$ adalah ...?
Catatan: Dua titik $P(a, \, b)$ dan $Q(c, \, d)$ berbeda jika $a \neq c$ dan $b \neq d$. Pasangan titik $(P, \, Q)$ dan $(Q, \, P)$ dianggap sama.
Nilai dari $b-a$ adalah ...?
Catatan: Untuk bilangan asli $k$, $\tau (k)$ menyatakan banyak faktor positif dari $k$.
Catatan: Titik tinggi suatu segitiga adalah perpotongan ketiga garis tinggi dari segitiga tersebut.
Kembali ke Daftar Isi Olimpiade Matik SMA
Kembali ke Solusi Singkat Olim Matik SD-SMP-SMA
Demikian artikel Solusi OSK Matematika SMA Tahun 2020 ini. Silahkan juga baca materi lain yang berkaitan dengan materi ini. Setiap artikel akan diupdate secara bertahap. Semoga bermanfaat. Terimakasih.