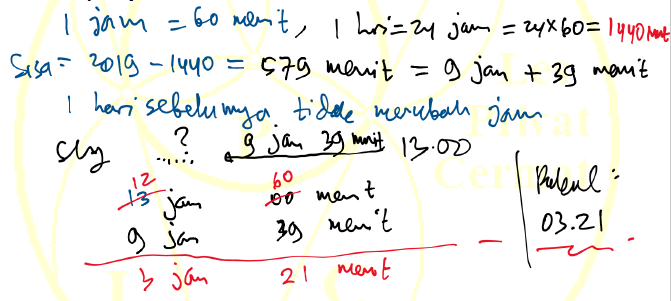Soal-soal dengan Solusi Singkat
1). Pak Budi memiliki sawah berbentuk huruf L. Jika diketahui bahwa
sawah Pak Budi hanya memiliki sisi yang panjangnya 5 meter dan 10
meter dan semua sudut sawahnya siku-siku, luas sawah Pak Budi
adalah ... meter persegi.
2). Jika sebuah jam sekarang menunjukkan pukul 13:00 maka 2019 menit
yang lalu jam tersebut menunjukkan pukul ...?
3). Kedua akar persamaan kuadrat $x^2 - 111x + k = 0$ adalah bilangan
prima. Nilai $k$ adalah ...?
4). Ani dan Banu bermain dadu enam sisi. Jika dadu yang keluar
bernilai genap, maka Ani mendapatkan skor 1 sedangkan jika dadu yang
keluar bernilai ganjil, maka Banu yang mendapatkan skor 1. Pemenang
dari permainan ini adalah orang pertama yang mendapatkan skor
total 5. Setelah dilakukan pelemparan dadu sebanyak 5 kali, Ani
mendapat skor 4 dan Banu mendapatkan skor 1. Peluang Ani memenangkan
permainan ini adalah ...?
5). Diketahui $a+2b = 1$, $b+2c = 2$, dan $b \neq 0$. Jika
$a+nb+2018c = 2019$, maka nilai $n$ adalah ...?
6). Misalkan $a = 2 \sqrt{2}- \sqrt{8-4 \sqrt{2}} $ dan
$b = 2 \sqrt{2} + \sqrt{8-4 \sqrt{2}}$ . Jika
$\frac{a}{b} + \frac{b}{a} = x + y \sqrt{2}$ dengan $x$, $y$ bulat,
maka nilai $x + y$ adalah ...?
7). Diberikan suatu trapesium ABCD dengan AB sejajar CD. Misalkan
titik P dan Q berturut-turut pada AD dan BC sedemikian sehingga PQ
sejajar AB dan membagi trapesium menjadi dua bagian yang sama
luasnya. Jika AB = 17 dan DC = 7 maka nilai PQ adalah ...?
8). Tujuh buah bendera dengan motif berbeda akan dipasang pada 4
tiang bendera. Pada masing-masing tiang bendera bisa dipasang
sebanyak nol, satu, atau lebih dari satu bendera. Banyaknya cara
memasang bendera tersebut adalah ...?
9). Misalkan $n$ adalah bilangan asli terkecil yang semua digitnya
sama dan sedikitnya terdiri dari 2019 digit. Jika $n$ habis dibagi
126, maka hasil penjumlahan semua digit dari $n$ adalah ...?
10). Untuk sebarang bilangan real $x$, simbol $\lfloor x \rfloor$
menyatakan bilangan bulat terbesar yang tidak lebih besar daripada
$x$, sedangkan $\lceil x \rceil$ menyatakan bilangan bulat terkecil
yang tidak lebih kedil dibandingkan $x$. Interval $[a, \, b)$ adalah
himpunan semua bilangan real $x$ yang memenuhi
$\, \, \, \, \, \, \, \lfloor 2x \rfloor ^2 = \lceil x \rceil + 7$.
Nilai $a.b$ adalah ...?
11). Sisa pembagian $1111^{2019}$ oleh 11111 adalah ...?
12). Diberikan segitiga ABC dengan D pertengahan AC, E pertengahan BD,
dan H merupakan pencerminan dari A terhadap E. Jika F perpotongan antara
AH dengan BC, maka nilai $\frac{AF}{FH}$ sama dengan ...?
13). Banyaknya bilangan delapan digit yang setiap digitnya adalah 1
atau 2 tepati tidak memuat tidak digit 1 berurutan adalah ...?
14). Misalkan $f(x) = 1 + \frac{90}{x}$. Nilai terbesar $x$ yang memenuhi
$\underbrace{f \left( f \left( ...\left( f(x) \right) ... \right) \right) }_{\text{2019 kali}} = x$ adalah ...?
15). Misalkan ABCD adalah persegi dengan panjang sisi 4.
Lingkaran-lingkaran $x$, $y$, $z$ dengan jari-jari sama mempunyai pusat
di dalam persegi sedemikian sehingga lingkaran $x$ menyinggung sisi AB
dan AD, lingkaran $y$ menyinggung sisi AB dan BC, serta lingkaran $z$
menyinggung sisi DC, lingkaran $x$, dan lingkaran $y$. Diketahui jari-jari
lingkaran $x$ dapat dinyatakan dengan $n - \sqrt{m}$ dengan $m$ dan $n$
bilangan bulat positif. Nilai $m$ adalah ...?
16). Semua bilangan bulat $n$ sehingga $n^4+16n^3+71n^2+56n$ merupakan
bilangan kuadrat tak nol adalah ...?
17). Diberikan jajargenjang ABCD, dengan $\angle ABC = 105^o$. Titik M
berada di dalam jajargenjang sehingga segitiga BMC sama sisi dan
$\angle CMD = 135^o$. Jika K pertengahan sisi AB, maka besarnya
$\angle BKC$ sama dengan ... derajat.
18). Bilangan real terbesar M sehingga untuk setiap $x$ positif berlaku
$\, \, \, \, \, (x+1)(x+3)(x+5)(x+11) \geq Mx$
adalah ...?
19). Banyaknya tripel bilangan bulat $(m, \, n, \, p)$ dengan $p$ prima
yang memenuhi
$\, \, \, \, \, p^2 n^2 - 3mn = 21p - m^2 $
adalah ...?
20). Suatu lomba matematika diikuti oleh 2019 peserta. Untuk setiap dua
peserta lomba, keduanya saling mengenal atau saling tidak mengenal.
Diketahui bahwa tidak ada tiga orang peserta lomba yang ketiganya saling
mengenal satu sama lain. Misalkan $m$ adalah bilangan asli sehingga:
(i). masing-masing peserta mengenal paling banyak $m$ peserta lainnya.
(ii). untuk seteiap bilangan asli $k$ dengan $1 \leq k \leq m$, minimal
terdapat satu orang peserta yang mengenal tepat $k$ peserta lainnya.
Nilai $m$ terbesar yang mungkin adalah ...?
Kembali ke
Daftar Isi Olimpiade Matik SMA
Kembali ke
Solusi Singkat Olim Matik SD-SMP-SMA
Demikian artikel
Solusi OSK Matematika SMA Tahun 2019 ini.
Silahkan juga baca materi lain yang berkaitan dengan materi ini. Setiap artikel akan diupdate secara bertahap. Semoga bermanfaat. Terimakasih.