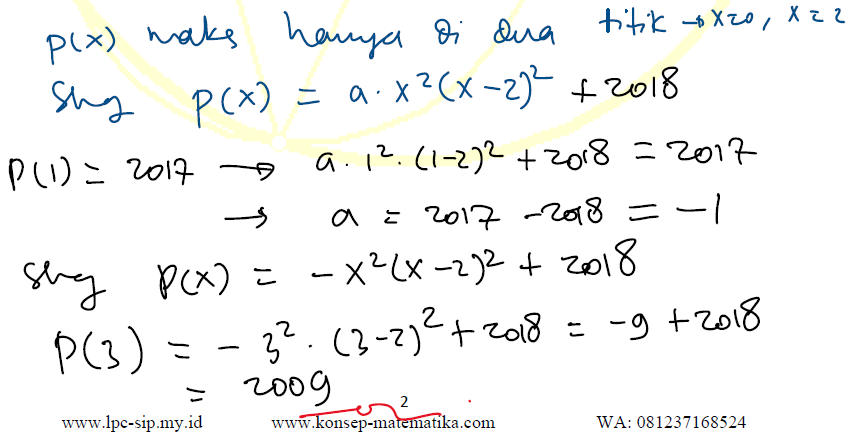Blog Koma - Hallow sahabat koma, bagaimana kabarnya hari ini? Semoga baik-baik saja ya.
Pada artikel ini kita akan membahas
Solusi OSK Matematika SMA Tahun 2017 sebagai pendukung dan menambah wawasan pemahaman
berbagai variasi soal-soal olimpiade matematika tingkat SMA khususnya soal-soal OSN-K. Dengan berlatih secara rutin dan giat dalam mempelajari
Soal dan Solusi OSK Matematika SMA Tahun 2017 yang ada, tentu sahabat koma akan lebih siap dalam menghadapi olimpiade atau kompetisi
matematika yang ada. Semangat terus untuk berlatih. Jika ada masukan atau ide atau cara lain mengenai
Solusi OSK Matematika SMA Tahun 2017 ini, mohon untuk dishare ke admin ya, biar terus ada perbaikan dan peningkatan
dari isi artikel yang ada di blog koma.

Soal-soal dengan Solusi Singkat
1). Diketahui $x-y=10$ dan $xy = 10$. Nilai $x^4+y^4$ adalah ...?
2). Empat siswa Adi, Budi, Cokro dan Dion bertanding balap sepeda. Kita hanya diberikan sebagian informasi sebagai berikut:
(a). setiap siswa sampai di garis finish pada waktu yang berlainan
(b). Adi bukan juara pertama
(c). Cokro kalah dari Budi
Dengan hanya mengetahui informasi ini saja, banyaknya susunan juara pertama, kedua, ketiga, dan keempat adalah ...?
3). Banyaknya bilangan asli $k$ yang memenuhi $k|(n^7-n)$ untuk semua
bilangan asli $n$ adalah ...?
4). Pada sebuah lingkaran dengan pusat O, talibusur AB berjarak 5 dari
titik O dan talibusur AC berjarak $5\sqrt{2}$ dari titik O. Jika
panjang jari-jari lingkaran 10, maka $BC^2$ adalah ...?
5). Jika $\frac{(a-b)(c-d)}{(b-c)(d-a)} = - \frac{4}{7}$, maka nilai
dari $\frac{(a-c)(b-d)}{(a-b)(c-d)} $ adalah ...?
6). Pada suatu kotak ada sekumpulan bola berwarna merah dan hitam yang
secara keseluruhannya kurang dari 1000 bola. Misalkan diambil dua bola.
Peluang terambilnya dua bola merah adalah $p$ dan peluang terambilnya
dua bola hitam adalah $q$ dengan $p - q = \frac{23}{37}$. Selisih
terbesar yang mungkin dari banyaknya bola merah dan hitam adalah ...?
7). Misalkan $s(n)$ menyatakan faktor prima terbesar dari $n$ dan $t(n)$
menyatakan faktor prima terkecil dari $n$. Banyaknya bilangan asli
$n \in \{1, \, 2, \, 3, \, , 100 \}$ sehingga $t(n)+1=s(n)$ adalah ...?
8). Semua titik sudut suatu persegi dengan panjang sisi $s$ terletak
pada batas dari juring lingkaran berjari-jari $r$ yang sudut pusatnya
$60^o$. Jika persegi diletakkan secara simetris di dalam juring, maka
nilai $\frac{r^2}{s^2}$ adalah ...?

9). Misalkan $a, \, b, \, c$ bilangan real positif yang memenuhi
$a+b+c = 1$. Nilai minimum dari $\frac{a+b}{abc}$ adalah ...?
10). Sebuah hotel mempunyai kamar bernomor 000 sampai dengan 999. Hotel
tersebut menerapkan aturan aneh sebagai berikut: jika suatu kamar
berisi tamu, dan sembarang dua digit nomor kamar tersebut dipertukarkan
tempatnya, maka diperoleh nomor kamar yang sama atau nomor kamar yang
tidak berisi tamu. Maksimal banyaknya kamar yang berisi tamu adalah ...?
11). Fungsi $f$ memetakan himpunan bilangan asli ke himpunan bilangan
bulat tak negatif. Fungsi tersebut memenuhi $f(1) = 0$ dan untuk setiap
bilangan asli berbeda $m, \, n$ dengan $m|n$, berlaku $f(m) < f(n)$.
Jika diketahui $f(8!) = 11$, maka nilai dari $f(2016)$ adalah ...?
12). Diberikan segitiga ABC dengan $AC = \frac{1}{2} (AB+BC)$. Misalkan
K dan M berturut-turut titik tengah AB dan BC. Titik L terletak pada
sisi AC sehingga BL adalah garis bagi sudut ABC. Jika $\angle ABC = 72^o$,
maka besarnya sudut KLM sama dengan ...?
13). Misalkan $P(x)$ suatu polinom berderajat 4 yang memiliki nilai
maksimum 2018 di $x = 0$ dan $x = 2$. Jika $P(1) = 2017$, maka nilai
$P(3)$ adalah ...?
14). Terdapat enam anak, A, B, C, D, E dan F, akan saling bertukar
kado. Tidak ada yang menerima kadonya sendiri, dan kado dari A
diberikan kepada B. banyaknya cara membagikan kado dengan cara
demikian adalah ...?
15). Bilangan asli terbesar $n$ sehingga $n!$ dapat dinyatakan sebagai
hasil perkalian dari $n-4$ bilangan asli berurutan adalah ...?
16). Pada segitiga ABC, titik K dan L berturut-turut adalah titik
tengah AB dan AC. Jika CK dan BL saling tegak lurus, maka nilai minimum
dari $\cot B + \cot C $ adalah ...?
17). Misalkan $a$, $b$, $c$ dan $d$ bilangan-bilangan bulat positif.
Jajargenjang yang dibatasi oleh garis-garis $y=ax+c$, $y=ax+d$, $y=bx+c$,
dan $y=bx+d$ mempunyai luas 18. Jajargenjang yang dibatasi oleh
garis-garis $y=ax+c$, $y=ax-d$, $y=bx+c$, dan $y=bx-d$ mempunyai luas 72.
Nilai terkecil yang mungkin untuk $a+b+c+d$ adalah ...?
18). Seratus bilangan bulat disusun mengelilingi lingkaran sedemikian
sehingga (menurut arah jarum jam) setiap bilangan lebih besar daripada
hasil penjumlahan dua bilangan sebelumnya. Maksimal banyaknya bilangan
bulat positif yang terdapat pada lingkaran tersebut adalah ...?
19). Untuk sebarang bilangan asli $n$, misalkan $S(n)$ adalah jumlah
digit-digit dari $n$ dalam penulisan desimal. Jika $S(n)=5$, maka nilai
maksimum dari $S(n^5)$ adalah ...?
20). Diberikan segitiga ABC dengan AB = 12, BC = 5 dan AC = 13.
Misalkan P suatu titik pada garis bagi $\angle A$ yang terletak di
dalam ABC dan misalkan M suatu titik pada sisi AB
(dengan $A \neq M \neq B$). Garis AP dan MP memotong BC dan AC
berturut-turut di D dan N. Jika $\angle MPB = \angle PCN$ dan
$\angle NPC = \angle MBP$, maka nilai $\frac{AP}{PD}$ adalah ...?
Kembali ke
Daftar Isi Olimpiade Matik SMA
Kembali ke
Solusi Singkat Olim Matik SD-SMP-SMA
Demikian artikel
Solusi OSK Matematika SMA Tahun 2017 ini.
Silahkan juga baca materi lain yang berkaitan dengan materi ini. Setiap artikel akan diupdate secara bertahap. Semoga bermanfaat. Terimakasih.