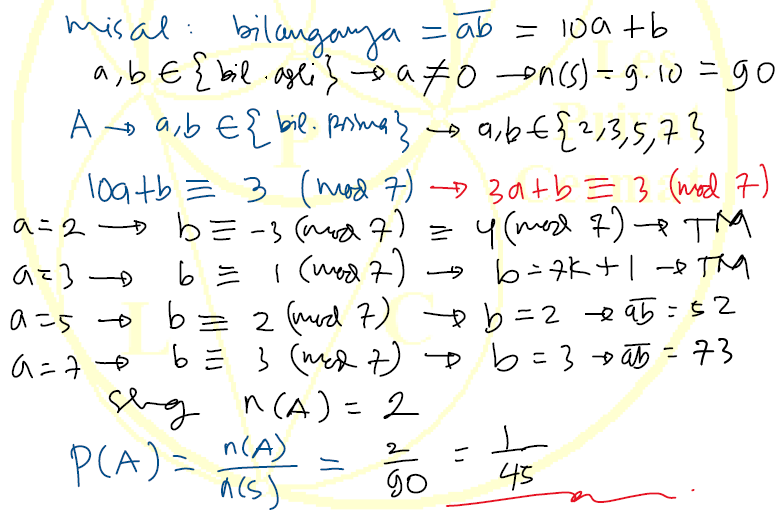Soal-soal dengan Solusi Singkat
1). Jika $a$, $b$, $c$, $d$, $e$ merupakan bilangan asli dengan
$a < 2b$, $b < 3c$, $c < 4d$, $d < 5e$ dan $e < 100$, maka nilai
maksimum dari $a$ adalah ...?
2). Rudi membuat bilangan asli dua digit. Probabilitas bahwa kedua
digit bilangan tersebut merupakan bilangan prima dan bilangan tersebut
bersisa 3 jika dibagi 7 adalah ...?
3). Pada segitga ABC, titik M terletak pada BC sehingga
AB = 7, AM = 3, BM = 5 dan MC = 6. Panjang AC adalah ...?
4). Diberikan $a$ dan $b$ bilangan real dengan
$\sqrt{a} - \sqrt{b} = 20$. Nilai maksimum dari $a-5b$ adalah ...?
5). Pada segitiga ABC, titik X, Y dan Z berturut-turut terletak pada
sinar BA, CB dan AC sehingga BX = 2BA, CY = 2CB dan AZ = 2AC. Jika
luas $\Delta$ABC adalah 1, maka luas $\Delta$XYZ adalah ...?
6). Banyak bilangan asli $n$ yang memenuhi sifat hasil jumlah $n$ dan
suatu pembagi positif $n$ yang kurang dari $n$ sama dengan 2016
adalah ...?
7). Misalkan $a$ adalah bilangan real sehingga polinomial
$p(x) = x^4 + 4x + a$ habis dibagi oleh $(x-c)^2$ untuk suatu bilangan
real $c$. Nilai $a$ yang memenuhi adalah ...?
8). Anak laki-laki dan anak perempuan yang berjumlah 48 orang duduk
melingkar secara acak. Banyaknya minimum anak perempuan sehingga pasti
ada enam anak perempuan yang duduk berdekatan tanpa diselingi anak
laki-laki adalah ...?
9). Misalkan $(a, \, b, \, c, \, d, \, e, \,f)$ adalah sebarang
pengurutan dari $(1, \, 2, \, 3, \, 4, \, 5, \, 6)$. Banyaknya
pengurutan sehingga $a+c+e > b+d+f $ adalah ...?
10). Misalkan $n_1, \, n_2, \, n_3, ... $ bilangan-bilangan asli yang
membentuk barisan aritmatika. Banyaknya nilai di himpunan
$\{ 1, \, 2, \,3 , \, ..., \, 1000 \}$ yang mungkin menjadi nilai
$n_{n_2} - n_{n_1} $ adalah ...?
11). Segitiga ABC mempunyai panjang sisi AB = 20, AC = 21 dan BC = 29.
Titik D dan E terletak pada segmen garis BC, dengan BD = 8 dan EC = 9.
Besar $\angle$DAE adalah ...?
12). Bilangan real $t$ sehingga terdapat dengan tunggal tripel bilangan
real $(x, \, y, \, z)$ yang memenuhi $x^2+2y^2 = 3z$ dan
$x+y+z = t$ adalah ...?
13). Palindrom adalah bilangan yang sama dibaca dari depan atau dari
belakang. Sebagai contoh 12321 dan 32223 merupakan palindrom. Palindrom
5 digit terbesar yang habis dibagi 303 adalah ...?
14). Diberikan barisan $\{ a_n \}$ dan $\{ b_n \}$ denga
$a_n = \frac{1}{n \sqrt{n} }$ dan
$b_n = \frac{1}{\left( 1+ \frac{1}{n} \right) +
\sqrt{1+ \frac{1}{n} } } $ untuk setiap bilangan asli $n$. misalkan
$S_n = a_1 b_1+a_2 b_2+ ... +a_n b_n$. Banyaknya bilangan asli $n$
dengan $n = 2016$ sehingga $S_n$ merupakan bilangan rasional adalah ...?
15). Diberikan persegi ABCD dengan panjang sisi 1. Titik K dan L
berturut-turut terletak pada segmen garis BC dan DC sehingga keliling
dari $\Delta$KCL adalah 2. Luas minimum dari $\Delta$AKL adalah ...?
16). Banyaknya pasangan terurut bilangan asli $(a, \, b, \, c)$
dengan $a, \, b, \, c \in \{ 1, \, 2, \, 3, \, 4, \, 5 \}$ sehingga
$\, \, \, \, \, \, \, \, \, \, max \{ a, \, b, \, c \} <
2 \, min \{a, \, b, \, c \} $
adalah ...?
17). Banyaknya bilangan asli $n \in \{ 1, \, 2, \, 3, \, ..., \, 1000 \}$
sehingga terdapat bilangan real positif $x$ yang memenuhi
$x^2 + \lfloor x \rfloor ^2 = n $ adalah ...?
18). Misalkan $x, \, y, \, z$ bilangan real positif yang memenuhi
$\, \, \, \, \, \, \, \, \, \,
3 \log _x (3y) = 3 \log _{3x} (27z) = \log _{3x^4}(81yz) \neq 0$.
Nilai dari $x^5 y^4 z$ adalah ...?
19). Diberikan empat titik pada satu lingkaran G dalam urutan
A, B, C, D. Sinar garis AB dan DC berpotongan di E, dan sinar garis AD
dan BC berpotongan di F. Misalkan EP dan FQ menyinggung lingkaran G
berturut-turut di P dan Q. Misalkan pula bahwa EP = 60 dan FQ = 63,
maka panjang EF adalah ...?
20). Pada sebuah bidang datar, terdapat 16 garis berbeda dan $n$ titik
potong berbeda. Nilai minimal $n$ sehingga dapat dipastikan terdapat 3
kelompok garis yang masing-masing memuat garis-garis berbeda yang
saling sejajar adalah ...?
Kembali ke
Daftar Isi Olimpiade Matik SMA
Kembali ke
Solusi Singkat Olim Matik SD-SMP-SMA
Demikian artikel
Solusi OSK Matematika SMA Tahun 2016 ini.
Silahkan juga baca materi lain yang berkaitan dengan materi ini. Setiap artikel akan diupdate secara bertahap. Semoga bermanfaat. Terimakasih.