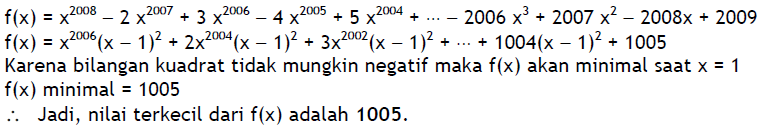Solusi OSN Matematika SMA Tahun 2009

          Blog Koma - Hallow sahabat koma, bagaimana kabarnya hari ini? Semoga baik-baik saja ya. Pada artikel ini kita akan membahas Solusi OSN Matematika SMA Tahun 2009 sebagai pendukung dan menambah wawasan pemahaman berbagai variasi soal-soal olimpiade matematika tingkat SMA. Dengan berlatih secara rutin dan giat dalam mempelajari Solusi OSN Matematika SMA Tahun 2009 yang ada, tentu sahabat koma akan lebih siap dalam menghadapi olimpiade atau kompetisi matematika yang ada. Semangat terus untuk berlatih. Jika ada masukan atau ide atau cara lain mengenai Solusi OSN Matematika SMA Tahun 2009 ini, mohon untuk dishare ke admin ya, biar terus ada perbaikan dan peningkatan dari isi artikel yang ada di blog koma.

Soal-soal dengan Solusi Singkat

Soal Hari Pertama: Soal Uraian

1). Tentukan banyaknya bilangan $n \in \{ 1, \,2, \,3, ..., \,2009\}$ sedemikian sehingga $4n^6+n^3+5$ habis dibagi 7.

Sumber: Eddy Hermanto, ST
Solusi Soal OSN Matematika SMA tahun 2009 nomor 1

2). Misalkan untuk setiap bilangan real $ x $ didefinisikan $\lfloor x \rfloor $ sebagai bilangan bulat terbesar yang lebih kecil atau sama dengan $x$. Diberikan $a_1, \, a_2, \, a_3, \, ...,$ suatu barisan bilangan asli yang memenuhi $a_1 > 1$ dan
$ \, \, \, \, \, \, \large {\lfloor \frac{a_1 +1}{a_2} \rfloor = \lfloor \frac{a_2 + 1}{a_3} \rfloor = \lfloor \frac{a_3 + 1}{a_4} \rfloor = .... } $
Buktikan bahwa
$ \, \, \, \, \, \, \large { \lfloor \frac{a_n + 1}{a_{n+1}} \rfloor \leq 1 }$
untuk setiap bilangan asli $n$.

Sumber: Eddy Hermanto, ST
Solusi Soal OSN Matematika SMA tahun 2009 nomor 2

3). Pada segitiga ABC, titik-titik D, E, dan F berturut-turut terletak pada segmen BC, CA, dan AB. Nyatakan P sebagai titik perpotongan AD dan EF. Tunjukkan bahwa
$ \, \, \, \, \, \, \, \, \, \, \, \frac{AB}{AF} \times DC + \frac{AC}{AE} \times DB = \frac{AD}{AP} \times BC $.

Sumber: Eddy Hermanto, ST
Solusi Soal OSN Matematika SMA tahun 2009 nomor 3

4). Di suatu pulau terdapat 7 kota dan ada jaringan kereta api yang melalui kota-kota tersebut. Setiap segmen rel menghubungkan tepat 2 kota, dan diketahui bahwa setiap kota memiliki paling sedikit 3 segmen ke kota lain. Buktikan bahwa terdapat rute perjalanan kereta api yang mengunjungi 4 kota yang berbeda masing-masing sekali dan kembali ke kota asalnya. (Contoh : rute $A - B - C - D - A$)

Sumber: Eddy Hermanto, ST
Solusi Soal OSN Matematika SMA tahun 2009 nomor 4

Soal Hari Kedua: Soal Uraian

5). Di dalam suatu laci terdapat paling banyak 2009 bola yang terdiri dari bola putih dan biru yang tercampur secara acak. Jika dua bola diambil secara acak tanpa pengembalian, maka diketahui probabilitas bahwa terambil keduanya bola warna putih atau keduanya bola warna biru adalah $\frac{1}{2} $. Berapa banyak maksimum bola putih yang mungkin berada dalam laci sedemikian sehingga pernyataan tentang probabilitas tersebut tetap terpenuhi?

Sumber: Eddy Hermanto, ST
Solusi Soal OSN Matematika SMA tahun 2009 nomor 5

6). Tentukan nilai terkecil yang mungkin dari fungsi
$ f(x)=x^{2008}-2x^{2007}+3x^{2006}-4x^{2005}$ +$5x^{2004}- ... -2006x^3+2007x^2-2008x+2009 $
untuk sebarang bilangan real $x$.

Sumber: Eddy Hermanto, ST
Solusi Soal OSN Matematika SMA tahun 2009 nomor 6

7). Suatu pasangan bilangan bulat $(m, \, n)$ dikatakan baik jika
$ \, \, \, \, \, \, \, \, m|(n^2+n)$ dan $n|(m^2+m)$.
Diberikan sebarang dua bilangan asli $a, \, b > 1$ yang relatif prima, buktikan bahwa terdapat pasangan baik $(m, \, n)$ dengan $a|m$ dan $b|n$ tetapi $a$ tidak membagi $n$ dan $b$ tidak membagi $m$.

Sumber: Eddy Hermanto, ST
Solusi Soal OSN Matematika SMA tahun 2009 nomor 7

8). Diberiikan segitiga ABC lancip. Lingkaran dalam segitiga ABC menyinggung BC, CA, dan AB berturut-turut di D, E, dan F. Garis bagi sudut A memotong DE dan DF berturut-turut di K dan L. Misalkan $AA_1$ adalah garis tinggi dan M titik tengah BC.
a). Buktikan bahwa BK dan CL tegak lurus garis bagi BAC.
b). Tunjukkan bahwa $A_1KML$ adalah segiempat talibusur.

Sumber: Eddy Hermanto, ST
Solusi Soal OSN Matematika SMA tahun 2009 nomor 8

Kembali ke Daftar Isi Olimpiade Matik SMA

Kembali ke Solusi Singkat Olim Matik SD-SMP-SMA

       Demikian artikel Solusi OSN Matematika SMA Tahun 2009 ini. Silahkan juga baca materi lain yang berkaitan dengan materi ini. Setiap artikel akan diupdate secara bertahap. Terimakasih.