Solusi OSN Matematika SMA Tahun 2008

          Blog Koma - Hallow sahabat koma, bagaimana kabarnya hari ini? Semoga baik-baik saja ya. Pada artikel ini kita akan membahas Solusi OSN Matematika SMA Tahun 2008 sebagai pendukung dan menambah wawasan pemahaman berbagai variasi soal-soal olimpiade matematika tingkat SMA. Dengan berlatih secara rutin dan giat dalam mempelajari Solusi OSN Matematika SMA Tahun 2008 yang ada, tentu sahabat koma akan lebih siap dalam menghadapi olimpiade atau kompetisi matematika yang ada. Semangat terus untuk berlatih. Jika ada masukan atau ide atau cara lain mengenai Solusi OSN Matematika SMA Tahun 2008 ini, mohon untuk dishare ke admin ya, biar terus ada perbaikan dan peningkatan dari isi artikel yang ada di blog koma.

Soal-soal dengan Solusi Singkat

Soal Hari Pertama: Soal Uraian

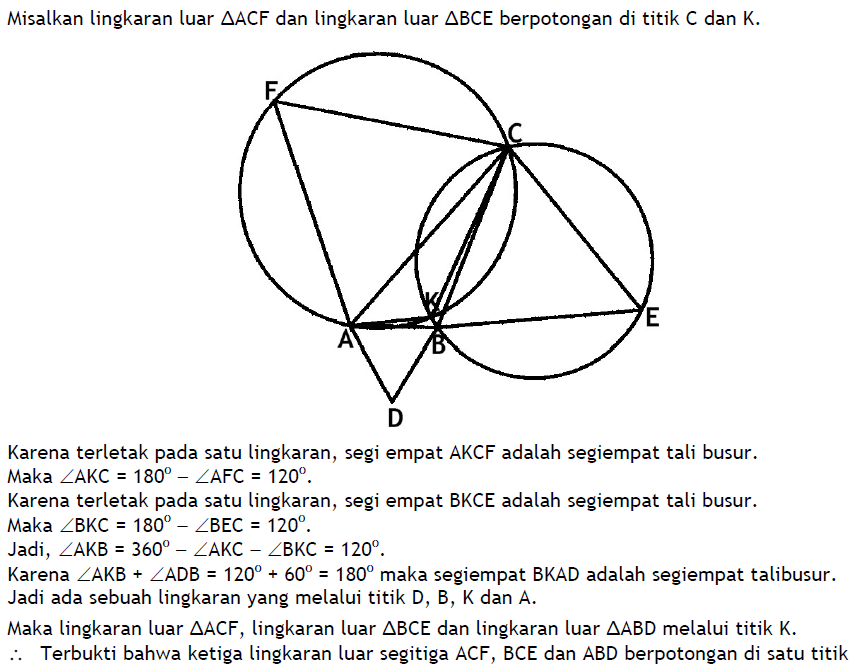
1). Diberikan segitiga ABC. Titik-titik D, E, dan F di luar segitiga ABC sedemikian sehingga segitiga ABD, segitiga BCE, dan segitiga CAF adalah segitiga sama sisi. Buktikan bahwa ketiga lingkaran luar segitiga tersebut berpotongan di satu titik.

Sumber: Eddy Hermanto, ST
Solusi Soal OSN Matematika SMA tahun 2008 nomor 1

2). Buktikan bahwa untuk $x$ dan $y$ bilangan real positif, berlaku
$\, \, \, \, \, \, \large { \frac{1}{(1+ \sqrt{x} \, )^2} + \frac{1}{(1+\sqrt{y} \, )^2} \geq \frac{2}{(x+y+2)} } $.

Sumber: Eddy Hermanto, ST
Solusi Soal OSN Matematika SMA tahun 2008 nomor 2

3). Carilah semua bilangan asli yang dapat dinyatakan dalam bentuk
$ \, \, \, \, \, \, \, \, \, \, \large { \frac{a+b}{c}+ \frac{b+c}{a}+ \frac{c+a}{b} }$
untuk suatu $a$, $b$, dan $c$ bilangan asli dengan
$ \, \, \, \, \, \, \, \, \, \, FPB(a, \, b)= FPB(b, \, c) =FPB(c, \,a)=1$.

Sumber: Eddy Hermanto, ST
Solusi Soal OSN Matematika SMA tahun 2008 nomor 3

4). Misalkan $A = \{1,\, 2, \, 3, \, ..., \, 2008 \}$.

a). Tentukan cacah subhimpunan dari $A$ yang hasil kali semua anggotanya habis dibagi 7.

b). Misalkan $N(i)$ menyatakan cacah subhimpunan dari $A$ yang jumlah semua anggotanya bersisa $i$ jika dibagi 7. Buktikan bahwa
$\, \, \, \, \, \, \, \, \, \, \large { \displaystyle{\sum_{i=0}^{7}} (-1)^i N(i) = 0 }$

Sumber: Eddy Hermanto, ST
Solusi Soal OSN Matematika SMA tahun 2008 nomor 4

Soal Hari Kedua: Soal Uraian

5). Misalkan $m$, $n > 1$ bilangan-bilangan bulat sedemikian hingga $n$ membagi $4^m-1$ dan $2^m$ membagi $n - 1$. Haruskah $n = 2^m+1$? Jelaskan.

Sumber: Eddy Hermanto, ST
Solusi Soal OSN Matematika SMA tahun 2008 nomor 5

6). Ada 21 orang berhubungan secara rahasia dengan menggunakan frekuensi gelombang radio yang berbeda. Ada pasangan dua orang yang dapat berhubungan, mungkin ada yang tidak dapat. Setiap pasang yang berhubungan hanya menggunakan satu frekuensi tertentu yang berbeda dengan frekuensi yang digunakan pasangan lain. Setiap tiga orang selalu ada dua orang di antaranya yang tidak dapat berhubungan. Tentukan banyak maksimum frekuensi berbeda yang diperlukan dan jelaskan.

Sumber: Eddy Hermanto, ST
Solusi Soal OSN Matematika SMA tahun 2008 nomor 6

7). Diberikan segitiga ABC dengan panjang sisi-sisinya $a$, $b$, dan $c$. Garis-garis singgung lingkaran dalam segitiga ABC yang sejajar dengan sisi-sisi segitiga ABC membentuk tiga segitiga kecil. Pada masing-masing segitiga kecil dibuat lingkaran dalam. Buktikan bahwa jumlah luas dari lingkaran dalam segitiga ABC dan ketiga lingkaran dalam segitiga kecil adalah
$\, \, \, \, \, \, \, \, \, \, \, \, \, \, \large { \frac{ (a^2+b^2+c^2)(b+c-a)(c+a-b)(a+b-c)}{(a+b+c)^3} }$

Sumber: Eddy Hermanto, ST
Solusi Soal OSN Matematika SMA tahun 2008 nomor 7

8). Tentukan semua fungsi $f:N \to N$ yang memenuhi
$\, \, \, \, \, \, \, \, \, \, \, \, f(mn)+f(m+n)=f(m)f(n)+1 $
untuk semua $m, \, n \in N$.

Sumber: Eddy Hermanto, ST
Solusi Soal OSN Matematika SMA tahun 2008 nomor 8

Kembali ke Daftar Isi Olimpiade Matik SMA

Kembali ke Solusi Singkat Olim Matik SD-SMP-SMA

       Demikian artikel Solusi OSN Matematika SMA Tahun 2008 ini. Silahkan juga baca materi lain yang berkaitan dengan materi ini. Setiap artikel akan diupdate secara bertahap. Terimakasih.