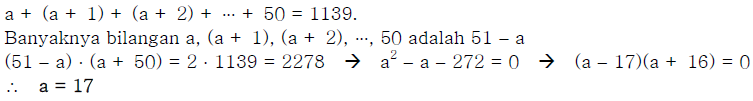Soal-soal dengan Solusi Singkat
1). Jumlah tiga bilangan prima pertama yang lebih besar dari 50 adalah ...
A. 169 B. 171 C. 173 D. 175 E. 177
2). Dalam sebuah kotak terdapat 5 bola merah dan 10 bola putih. Jika diambil dua bola
secara bersamaan, peluang memperoleh dua bola berwarna sama adalah ...
A. 1/2 B. 1/4 C. 2/21 D. 10/21 E. 11/21
3). Jika $X = \frac{1}{2+\frac{1}{2 + \frac{1}{2}}}$, maka $X = ... $
A. 2/9 B. 5/12 C. 4/9 D. 9/4 E. 12/5
4). Pada segitiga ABC, titik F membagi sisi AC dalam perbandingan $1:2$. Misalkan G
titik tengah BF dan E titik perpotongan antara sisi BC dengan AG. Maka titik E membagi
sisi BC dalam perbandingan
A. 1:4 B. 1:3 C. 2:5 D. 4:11 E. 3:8
5). Dalam suatu pertemuan terjadi 28 jabat tangan (salaman). Setiap dua orang saling
berjabat tangan paling banyak sekali. Banyaknya orang yang hadir dalam pertemuan
tersebut paling sedikit adalah ...
A. 28 B. 27 C. 14 D. 8 E. 7
6). Gaji David lebih banyak 20% daripada gaji Andika. Ketika Andika memperoleh kenaikan
gaji, gajinya menjadi lebih banyak 20% daripada gaji David. Persentase kenaikan gaji
Andika adalah ...
A. 0, 44 B. 20 C. 44 D. 144
E. tidak dapat ditentukan dengan pasti
7). Misalkan $T$ adalah himpunan semua titik pada bidang-$xy$ yang memenuhi $|x|+|y| = 4$.
Luas daerah $T$ adalah ...
A. 4 B. 8 C. 12 D. 16 E. 32
8). Definisikan $a * b = a + b + 1$, untuk semua bilangan bulat $a$, $b$. Jika $p$
memenuhi $a * p = a$, untuk setiap bilangan bulat $a$, maka $p = ... $
A. -1 B. 0 C. 1 D. 2
E. tidak ada yang memenuhi
9). Setiap dong adalah ding, dan beberapa dung juga dong.
X: Terdapat dong yang ding sekaligus dung.
Y: Beberapa ding adalah dung.
Z: Terdapat dong yang bukan dung.
A. Hanya X yang benar
B. Hanya Y yang benar
C. Hanya Z yang benar
D. X dan Y keduanya benar
E. X, Y, dan Z semuanya salah
10). Banyaknya solusi pasangan bilangan bulat positif persamaan $3x + 5y = 501$
adalah ...
A. 33 B. 34 C. 35 D. 36 E. 37
11). Diketahui $a + (a + 1) + (a + 2) + ... + 50 = 1139$. Jika $a$ bilangan positif,
maka $a = ... $
12). Di antara lima orang gadis, Arinta, Elsi, Putri, Rita, dan Venny, dua orang
memakai rok dan tiga orang memakai celana panjang. Arinta dan Putri mengenakan jenis
pakaian yang sama. Jenis pakaian Putri dan Elsi berbeda, demikian pula dengan Elsi dan
Rita. Kedua gadis yang memakai rok adalah ...
13). Barisan 2, 3, 5, 6, 7, 10, 11, ... terdiri dari semua bilangan asli yang bukan
kuadrat atau pangkat tiga bilangan bulat. Suku ke-250 barisan adalah ...
14). Jika $f(xy) = f(x + y)$ dan $f(7) = 7$, maka $f(49) = ... $
15). Pada sebuah barisan aritmatika, nilai suku ke-25 tiga kali nilai suku ke-5.
Suku yang bernilai dua kali nilai suku pertama adalah suku ke ...
16). Dimas membeli majalah setiap 5 hari sekali, sedangkan Andre membeli majalah setiap
8 hari sekali. Kemarin Dimas membeli majalah. Andre membeli majalah hari ini. Keduanya
paling cepat akan membeli majalah pada hari yang sama ... hari lagi.
17). Nanang mencari semua bilangan empat-angka yang selisihnya dengan jumlah keempat
angkanya adalah 2007. Banyaknya bilangan yang ditemukan Nanang tidak akan lebih
dari ...
18). Parabola $y = ax^2 + bx + c$ memiliki puncak dengan koordinat $(4,\, 2)$. Jika
titik $(2, \, 0)$ terletak pada parabola, maka $abc = ... $
19). Sebuah garis $\ell _1$ mempunyai kemiringan $- 2$ dan melalui titik $(p, \, -3)$.
Sebuah garis lainnya, $\ell _2$, tegak lurus terhadap $\ell _1$ di titik $(a, \, b)$
dan melalui titik $(6, \, p)$. Bila dinyatakan dalam $p$, maka $a = ... $
20). Pada segitiga ABC yang tumpul di C, titik M adalah titik tengah AB. Melalui C
dibuat garis tegak lurus pada BC yang memotong AB di titik E. Dari M tarik garis
memotong BC tegak lurus di D. Jika luas segitiga ABC adalah 54 satuan luas, maka luas
segitiga BED adalah ...
Kembali ke
Daftar Isi Olimpiade Matik SMA
Kembali ke
Solusi Singkat Olim Matik SD-SMP-SMA
Demikian artikel
Solusi OSK Matematika SMA Tahun 2006 ini.
Silahkan juga baca materi lain yang berkaitan dengan materi ini. Setiap artikel akan diupdate secara bertahap. Semoga bermanfaat. Terimakasih.