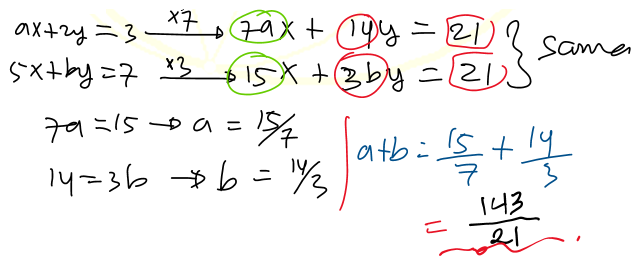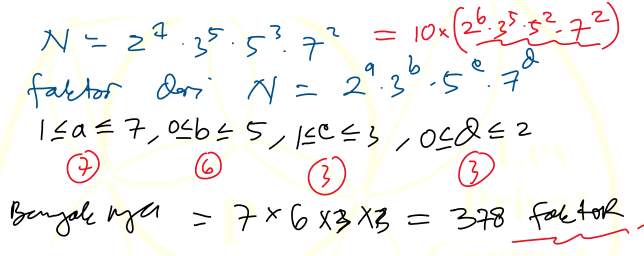Blog Koma - Hallow sahabat koma, bagaimana kabarnya hari ini? Semoga baik-baik saja ya.
Pada artikel ini kita akan membahas Solusi Singkat Soal OSK 2011 bagian II Olim SMA sebagai pendukung dan menambah wawasan pemahaman
berbagai variasi soal-soal olimpiade matematika tingkat SMA. Dengan berlatih secara rutin dan giat dalam mempelajari
Soal dan Solusi Soal OSK Olim Matik SMA yang ada, tentu sahabat koma akan lebih siap dalam menghadapi olimpiade atau kompetisi
matematika yang ada. Semangat terus untuk berlatih. Jika ada masukan atau ide atau cara lain mengenai
Solusi Singkat Soal OSK 2011 bagian II Olim SMA ini, mohon untuk dishare ke admin ya, biar terus ada perbaikan dan peningkatan
dari isi artikel yang ada di blog koma.
1). Tentukan semua bilangan bulat positif $p$ sedemikian sehingga $p$, $p+8$, dan $p+16$ adalah prima?
2). Jika $A=5^x+5^{-x} $ dan $B=5^x-5^{-x}$, maka $A^2 - B^2$ adalah ...?
3). Diketahui segitiga ABC, titik D dan E berturut-turut pada sisi AB dan AC, dengan panjang $AD=\frac{1}{2} BD$ dan $AE= \frac{1}{2}CE$. Garis BE dan CD berpotongan di titik F. diketahui luas segitiga ABC adalah 90 cm$^2$. Luas segiempat ADFE adalah ...?
4). Ada berapa banyak bilangan bulat positif berlambang "$abcde$" dengan $a < b \leq c < d < e$?
5). Bilangan asli terkecil lebih dari 2011 yang bersisa 1 jika dibagi 2, 3, 4, 5, 6, 7, 8, 9, dan 10 adalah ...?
6). Bilangan bulat positif terkecil $a$ sehingga $2a+4a+6a+ ... +200a$ merupakan kuadrat sempurna adalah ...?
7). Misalkan $A$ dan $B$ adalah sudut-sudut lancip yang memenuhi $\tan (A+B)= \frac{1}{2} $ dan $\tan (A-B)= \frac{1}{3}$. Besar sudut $A$ adalah ...?
8). Jika $ax+2y=3$ dan $5x+by=7$ menyatakan persamaan garis yang sama, maka $a+b= ...$?
9). Terdapat 5 orang pria dan 5 orang wanita duduk dalam sederetan kursi secara random. Berapa banyaknya cara untuk menduduki kursi tersebut, dengan syarat tidak boleh ada yang duduk berdampingan dengan jenis kelamin yang sama?
10). Ada berapa faktor positif dari $2^7 3^5 5^3 7^2$ yang merupakan kelipatan 10?
1). Tentukan semua bilangan bulat positif $p$ sedemikian sehingga $p$, $p+8$, dan $p+16$ adalah prima?
2). Jika $A=5^x+5^{-x} $ dan $B=5^x-5^{-x}$, maka $A^2 - B^2$ adalah ...?
3). Diketahui segitiga ABC, titik D dan E berturut-turut pada sisi AB dan AC, dengan panjang $AD=\frac{1}{2} BD$ dan
$AE= \frac{1}{2}CE$. Garis BE dan CD berpotongan di titik F. diketahui luas segitiga ABC adalah 90 cm$^2$.
Luas segiempat ADFE adalah ...?
4). Ada berapa banyak bilangan bulat positif berlambang "$abcde$" dengan $a < b \leq c < d < e$?
5). Bilangan asli terkecil lebih dari 2011 yang bersisa 1 jika dibagi 2, 3, 4, 5, 6, 7, 8, 9, dan 10 adalah ...?
6). Bilangan bulat positif terkecil $a$ sehingga $2a+4a+6a+ ... +200a$ merupakan kuadrat sempurna adalah ...?
7). Misalkan $A$ dan $B$ adalah sudut-sudut lancip yang memenuhi $\tan (A+B)= \frac{1}{2} $ dan $\tan (A-B)= \frac{1}{3}$.
Besar sudut $A$ adalah ...?
8). Jika $ax+2y=3$ dan $5x+by=7$ menyatakan persamaan garis yang sama, maka $a+b= ...$?
9). Terdapat 5 orang pria dan 5 orang wanita duduk dalam sederetan kursi secara random. Berapa banyaknya cara untuk menduduki kursi tersebut,
dengan syarat tidak boleh ada yang duduk berdampingan dengan jenis kelamin yang sama?
10). Ada berapa faktor positif dari $2^7 3^5 5^3 7^2$ yang merupakan kelipatan 10?
Kembali ke Daftar Isi Olimpiade Matik SMA
Kembali ke Solusi Singkat Olim Matik SD-SMP-SMA
Demikian artikel Solusi Singkat Soal OSK 2011 bagian II Olim SMA ini. Silahkan juga baca materi lain yang berkaitan dengan materi ini. Setiap artikel akan diupdate secara bertahap. Jika ada kritik dan saran, atau koreksi dari isi artikel di halaman ini, mohon bantuannya untuk menuliskannya di kolom komentar di bagian bawah setiap artikel. Ini sangat membantu untuk memperbaiki kualitas dari artikel di blog koma. Semoga bermanfaat. Terimakasih.
Soal-soal Tanpa Solusi
1). Tentukan semua bilangan bulat positif $p$ sedemikian sehingga $p$, $p+8$, dan $p+16$ adalah prima?
2). Jika $A=5^x+5^{-x} $ dan $B=5^x-5^{-x}$, maka $A^2 - B^2$ adalah ...?
3). Diketahui segitiga ABC, titik D dan E berturut-turut pada sisi AB dan AC, dengan panjang $AD=\frac{1}{2} BD$ dan $AE= \frac{1}{2}CE$. Garis BE dan CD berpotongan di titik F. diketahui luas segitiga ABC adalah 90 cm$^2$. Luas segiempat ADFE adalah ...?
4). Ada berapa banyak bilangan bulat positif berlambang "$abcde$" dengan $a < b \leq c < d < e$?
5). Bilangan asli terkecil lebih dari 2011 yang bersisa 1 jika dibagi 2, 3, 4, 5, 6, 7, 8, 9, dan 10 adalah ...?
6). Bilangan bulat positif terkecil $a$ sehingga $2a+4a+6a+ ... +200a$ merupakan kuadrat sempurna adalah ...?
7). Misalkan $A$ dan $B$ adalah sudut-sudut lancip yang memenuhi $\tan (A+B)= \frac{1}{2} $ dan $\tan (A-B)= \frac{1}{3}$. Besar sudut $A$ adalah ...?
8). Jika $ax+2y=3$ dan $5x+by=7$ menyatakan persamaan garis yang sama, maka $a+b= ...$?
9). Terdapat 5 orang pria dan 5 orang wanita duduk dalam sederetan kursi secara random. Berapa banyaknya cara untuk menduduki kursi tersebut, dengan syarat tidak boleh ada yang duduk berdampingan dengan jenis kelamin yang sama?
10). Ada berapa faktor positif dari $2^7 3^5 5^3 7^2$ yang merupakan kelipatan 10?
Soal-soal dengan Solusi Singkat
1). Tentukan semua bilangan bulat positif $p$ sedemikian sehingga $p$, $p+8$, dan $p+16$ adalah prima?
Kembali ke Daftar Isi Olimpiade Matik SMA
Kembali ke Solusi Singkat Olim Matik SD-SMP-SMA
Demikian artikel Solusi Singkat Soal OSK 2011 bagian II Olim SMA ini. Silahkan juga baca materi lain yang berkaitan dengan materi ini. Setiap artikel akan diupdate secara bertahap. Jika ada kritik dan saran, atau koreksi dari isi artikel di halaman ini, mohon bantuannya untuk menuliskannya di kolom komentar di bagian bawah setiap artikel. Ini sangat membantu untuk memperbaiki kualitas dari artikel di blog koma. Semoga bermanfaat. Terimakasih.