Blog Koma - Hallow sahabat koma, bagaimana kabarnya hari ini? Semoga baik-baik saja ya.
Pada artikel ini kita akan membahas Solusi Singkat Soal OSK 2003 Bagian II Olim SMA sebagai pendukung dan menambah wawasan pemahaman
berbagai variasi soal-soal olimpiade matematika tingkat SMA. Dengan berlatih secara rutin dan giat dalam mempelajari
Soal dan Solusi Soal OSK-OSP-OSN Olim Matik SMA yang ada, tentu sahabat koma akan lebih siap dalam menghadapi olimpiade atau kompetisi
matematika yang ada. Semangat terus untuk berlatih. Jika ada masukan atau ide atau cara lain mengenai
Solusi Singkat Soal OSK 2003 Bagian II Olim SMA ini, mohon untuk dishare ke admin ya, biar terus ada perbaikan dan peningkatan
dari isi artikel yang ada di blog koma.
1. Misalkan $f$ adalah fungsi yang memenuhi $f \left( \frac{1}{x} \right) + \frac{1}{x} f(-x)=2x $ untuk semua $x \neq 0$. Berapa $f(2)$?
2. Jika $a^2-b^2=2003 $ dengan $a, b$ bilangan bulat. Berapa nilai $a^2+b^2$?
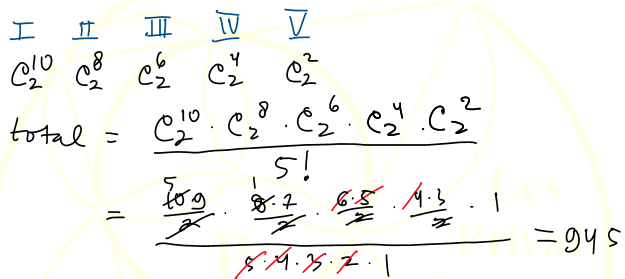
3. Dari sepuluh siswa dibentuk 5 kelompok, masing-masing beranggota 2 orang. Berapa cara membentuk 5 orang ini?
4. Misalkan $f(x) = x^5+ax^4+bx^3+cx^2+dx+e $ dan $ f(1)=f(2)=f(3)=f(4)=f(5) $. Berapa nilai $a$?
5. Tentukan $ \left( 1 - \frac{1}{2^2} \right) \left( 1 - \frac{1}{3^2} \right) \left( 1 - \frac{1}{4^2} \right) ... \left( 1 - \frac{1}{2003^2} \right)$.
6. Iwan selalu berbohong pada hari Senin, Selasa, Rabu dan jujur pada hari lainnya. Budi selalu berbohong pada hari Kamis, Jumat, Sabtu dan jujur pada hari lainnya. Pada suatu hari, Iwan berkata, "Kemarin saya berbohong." Budi berkata, "Saya juga." Pada hari apa percakapan tersebut terjadi?
7. Segitiga ABC sama sisi dengan panjang sisi 1 satuan. Melalui B dibuat garis tegak lurus BC. Garis itu berpotongan dengan AC di D. Berapa panjang BD?
8. Untuk setiap bilanga real $p$, kita definisikan $\lfloor p \rfloor $ sebagai bilangan bulat terbesar yang kurang dari atau sama dengan $p$. Sebagai contoh $ \lfloor 4,9 \rfloor = 4 $ dan $ \lfloor 7 \rfloor = 7$. Jika $x$ dan $y$ bilangan real sehingga $ \lfloor \sqrt{x} \rfloor =9 $ dan $ \lfloor \sqrt{y} \rfloor = 12$, maka nilai terkecil yang mungkin dicapai oleh $ \lfloor y-x \rfloor $ adalah ...?
9. Untuk menentukan wakilnya dalam cabang lari 110 m gawang putera, sebuah SMU mengadakan seleksi yang diikuti 5 orang siswa. Dalam seleksi tersebut diadakan tiga kali lomba yang pada setiap lomba, pelari tercepat diberi nilai 5, sedangkan peringkat di bawahnya berturut-turut mendapat nilai 3, 2, 1, 1. Tidak ada dua pelari yang menempati peringkat yang sama. Jika pemenang seleksi diberikan kepada yang nilai totalnya paling tinggi pada ketiga lomba, berapakah nilai terendah yang mungkin dicapai oleh pemenang seleksi?
10. Misalkan $a, b, c, d, e, f, g, h, i$ adalah bilangan-bilangan asli berbeda yang kurang atau sama dengan 9. Jika jumlah tiga bilangan dalam setiap lingkaran nilainya sama, tentukan nilai $a+d+g$?

1. Misalkan $f$ adalah fungsi yang memenuhi $f \left( \frac{1}{x} \right) + \frac{1}{x} f(-x)=2x $ untuk semua $x \neq 0$. Berapa $f(2)$?
2. Jika $a^2-b^2=2003 $ dengan $a, b$ bilangan bulat. Berapa nilai $a^2+b^2$?
3. Dari sepuluh siswa dibentuk 5 kelompok, masing-masing beranggota 2 orang. Berapa cara membentuk 5 orang ini?
4. Misalkan $f(x) = x^5+ax^4+bx^3+cx^2+dx+e $ dan $ f(1)=f(2)=f(3)=f(4)=f(5) $. Berapa nilai $a$?
5. Tentukan $ \left( 1 - \frac{1}{2^2} \right) \left( 1 - \frac{1}{3^2} \right) \left( 1 - \frac{1}{4^2} \right) ... \left( 1 - \frac{1}{2003^2} \right)$.
6. Iwan selalu berbohong pada hari Senin, Selasa, Rabu dan jujur pada hari lainnya. Budi selalu berbohong pada hari Kamis, Jumat, Sabtu dan
jujur pada hari lainnya. Pada suatu hari, Iwan berkata, "Kemarin saya berbohong." Budi berkata, "Saya juga." Pada hari apa percakapan tersebut
terjadi?
7. Segitiga ABC sama sisi dengan panjang sisi 1 satuan. Melalui B dibuat garis tegak lurus BC. Garis itu berpotongan dengan AC di D.
Berapa panjang BD?
8. Untuk setiap bilanga real $p$, kita definisikan $\lfloor p \rfloor $ sebagai bilangan bulat terbesar yang kurang dari atau sama dengan $p$.
Sebagai contoh $ \lfloor 4,9 \rfloor = 4 $ dan $ \lfloor 7 \rfloor = 7$. Jika $x$ dan $y$ bilangan real sehingga
$ \lfloor \sqrt{x} \rfloor =9 $ dan $ \lfloor \sqrt{y} \rfloor = 12$, maka nilai terkecil yang mungkin dicapai
oleh $ \lfloor y-x \rfloor $ adalah ...?
9. Untuk menentukan wakilnya dalam cabang lari 110 m gawang putera, sebuah SMU mengadakan seleksi yang diikuti 5 orang siswa. Dalam seleksi
tersebut diadakan tiga kali lomba yang pada setiap lomba, pelari tercepat diberi nilai 5, sedangkan peringkat di bawahnya berturut-turut
mendapat nilai 3, 2, 1, 1. Tidak ada dua pelari yang menempati peringkat yang sama. Jika pemenang seleksi diberikan kepada yang nilai totalnya
paling tinggi pada ketiga lomba, berapakah nilai terendah yang mungkin dicapai oleh pemenang seleksi?
10. Misalkan $a, b, c, d, e, f, g, h, i$ adalah bilangan-bilangan asli berbeda yang kurang atau sama dengan 9. Jika jumlah tiga bilangan dalam
setiap lingkaran nilainya sama, tentukan nilai $a+d+g$?

Kembali ke Daftar Isi Olimpiade Matik SMA
Kembali ke Solusi Singkat Olim Matik SD-SMP-SMA
Demikian artikel Solusi Singkat Soal OSK 2003 Bagian II Olim SMA ini. Silahkan juga baca materi lain yang berkaitan dengan materi ini. Setiap artikel akan diupdate secara bertahap. Jika ada kritik dan saran, atau koreksi dari isi artikel di halaman ini, mohon bantuannya untuk menuliskannya di kolom komentar di bagian bawah setiap artikel. Ini sangat membantu untuk memperbaiki kualitas dari artikel di blog koma. Semoga bermanfaat. Terimakasih.
Soal-soal Tanpa Solusi
1. Misalkan $f$ adalah fungsi yang memenuhi $f \left( \frac{1}{x} \right) + \frac{1}{x} f(-x)=2x $ untuk semua $x \neq 0$. Berapa $f(2)$?
2. Jika $a^2-b^2=2003 $ dengan $a, b$ bilangan bulat. Berapa nilai $a^2+b^2$?
3. Dari sepuluh siswa dibentuk 5 kelompok, masing-masing beranggota 2 orang. Berapa cara membentuk 5 orang ini?
4. Misalkan $f(x) = x^5+ax^4+bx^3+cx^2+dx+e $ dan $ f(1)=f(2)=f(3)=f(4)=f(5) $. Berapa nilai $a$?
5. Tentukan $ \left( 1 - \frac{1}{2^2} \right) \left( 1 - \frac{1}{3^2} \right) \left( 1 - \frac{1}{4^2} \right) ... \left( 1 - \frac{1}{2003^2} \right)$.
6. Iwan selalu berbohong pada hari Senin, Selasa, Rabu dan jujur pada hari lainnya. Budi selalu berbohong pada hari Kamis, Jumat, Sabtu dan jujur pada hari lainnya. Pada suatu hari, Iwan berkata, "Kemarin saya berbohong." Budi berkata, "Saya juga." Pada hari apa percakapan tersebut terjadi?
7. Segitiga ABC sama sisi dengan panjang sisi 1 satuan. Melalui B dibuat garis tegak lurus BC. Garis itu berpotongan dengan AC di D. Berapa panjang BD?
8. Untuk setiap bilanga real $p$, kita definisikan $\lfloor p \rfloor $ sebagai bilangan bulat terbesar yang kurang dari atau sama dengan $p$. Sebagai contoh $ \lfloor 4,9 \rfloor = 4 $ dan $ \lfloor 7 \rfloor = 7$. Jika $x$ dan $y$ bilangan real sehingga $ \lfloor \sqrt{x} \rfloor =9 $ dan $ \lfloor \sqrt{y} \rfloor = 12$, maka nilai terkecil yang mungkin dicapai oleh $ \lfloor y-x \rfloor $ adalah ...?
9. Untuk menentukan wakilnya dalam cabang lari 110 m gawang putera, sebuah SMU mengadakan seleksi yang diikuti 5 orang siswa. Dalam seleksi tersebut diadakan tiga kali lomba yang pada setiap lomba, pelari tercepat diberi nilai 5, sedangkan peringkat di bawahnya berturut-turut mendapat nilai 3, 2, 1, 1. Tidak ada dua pelari yang menempati peringkat yang sama. Jika pemenang seleksi diberikan kepada yang nilai totalnya paling tinggi pada ketiga lomba, berapakah nilai terendah yang mungkin dicapai oleh pemenang seleksi?
10. Misalkan $a, b, c, d, e, f, g, h, i$ adalah bilangan-bilangan asli berbeda yang kurang atau sama dengan 9. Jika jumlah tiga bilangan dalam setiap lingkaran nilainya sama, tentukan nilai $a+d+g$?

Soal-soal dengan Solusi Singkat
1. Misalkan $f$ adalah fungsi yang memenuhi $f \left( \frac{1}{x} \right) + \frac{1}{x} f(-x)=2x $ untuk semua $x \neq 0$. Berapa $f(2)$?

Kembali ke Daftar Isi Olimpiade Matik SMA
Kembali ke Solusi Singkat Olim Matik SD-SMP-SMA
Demikian artikel Solusi Singkat Soal OSK 2003 Bagian II Olim SMA ini. Silahkan juga baca materi lain yang berkaitan dengan materi ini. Setiap artikel akan diupdate secara bertahap. Jika ada kritik dan saran, atau koreksi dari isi artikel di halaman ini, mohon bantuannya untuk menuliskannya di kolom komentar di bagian bawah setiap artikel. Ini sangat membantu untuk memperbaiki kualitas dari artikel di blog koma. Semoga bermanfaat. Terimakasih.