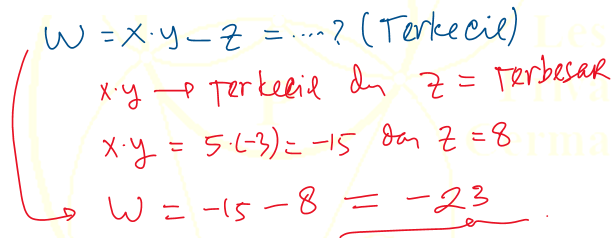Blog Koma - Hallow sahabat koma, bagaimana kabarnya hari ini? Semoga baik-baik saja ya.
Pada artikel ini kita akan membahas Solusi Singkat Soal OSK 2002 Bagian II Olim SMP sebagai pendukung dan menambah wawasan pemahaman
berbagai variasi soal-soal olimpiade matematika tingkat SMP. Dengan berlatih secara rutin dan giat dalam mempelajari
Soal dan Solusi Soal OSK-OSP-OSN Olim Matik SMP yang ada, tentu sahabat koma akan lebih siap dalam menghadapi olimpiade atau kompetisi
matematika yang ada. Semangat terus untuk berlatih. Jika ada masukan atau ide atau cara lain mengenai
Solusi Singkat Soal OSK 2002 Bagian II Olim SMP ini, mohon untuk dishare ke admin ya, biar terus ada perbaikan dan peningkatan
dari isi artikel yang ada di blog koma.
1). Misalkan titik A terletak pada garil L yaitu $y=5x+3$. Koordinat titik B adalah $(3,-2)$. Jika T adalah titik tengah dari AB sehingga AB tegak lurus dengan garis L, tentukan persamaan garis yang sejajar L dan melalui T!
2). Suatu angkutan kota mempunyai aturan pembayaran sebagai berikut. Pada saat naik setiap penumpang harus membayar Rp. 600, setelah 4 km pertama harus membayar Rp. 1.400, dan setiap menempuh 2 km berikutnya harus membayar Rp. 150 dan membayar Rp 100 setelah 1 km. Budi menaiki angkutan kota tersebut sejauh 21 km, berapakah Budi minimal harus membayar jasa angkutan kota tersebut?
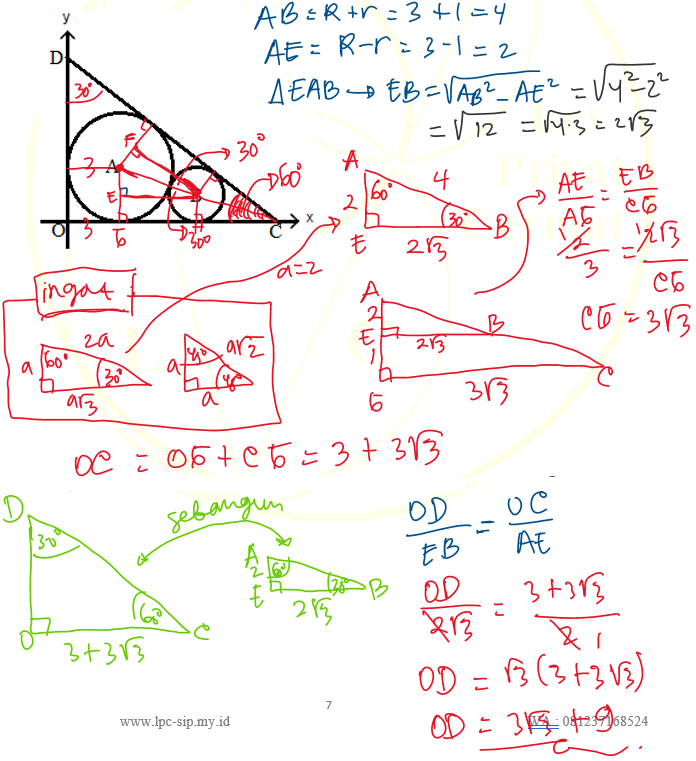
3). Lingkaran dengan pusat A berjari-jari 3 dan lingkaran dengan pusat B berjari-jari 1 seperti pada gambar. Berapakah jarak dari O ke D?

4). Perhatikan gambar di bawah ini! Segitiga ABC sama kaki dengan AB = AC dan BC = 30 cm. persegi EFGH mempunyai panjang sisi 12 cm. Berapakah luas segitiga AEF?

5). Jika gambar di bawah ini menunjukan lipatan untuk membuat kubus, huruf apakah yang berhadapan dengan huruf G?

6). Dalam bujur sangkar ajaib seperti pada gambar, jumlah angka pada setiap baris, kolom dan diagonal adalah sama. Berapakah jumlah tiga angka dari sembarang barisnya?

7). Jika panjang sisi persegi ABCD 1 cm, berapakah luas bangun yang diarsir?

8). Jika $x$ dan $y$ dua bilangan positif dan rata-rata dari 4, 20, dan $x$ adalah sama dengan rata-rata dari $y$ dan 16. Berapakah rasio dari $x$ dan $y$?
9). Jika $ -2 \leq x \leq 5$, $-3 \leq y \leq 5$, $4 \leq z \leq 8$ dan $w=xy-z$, berapakah nilai terkecil dari $w$ yang memenuhi?
10). Suatu daerah dibatasi oleh persamaan $y=2x+2$, $y= \frac{1}{2}x + 1$ dan $y=- \frac{3}{4} x+7$. Berapakah nilai maksimum $y$ pada daerah tersebut?
1). Misalkan titik A terletak pada garil L yaitu $y=5x+3$. Koordinat titik B adalah $(3,-2)$. Jika T adalah titik tengah dari AB sehingga AB tegak lurus dengan garis L, tentukan persamaan garis yang sejajar L dan melalui T!
2). Suatu angkutan kota mempunyai aturan pembayaran sebagai berikut. Pada saat naik setiap penumpang harus membayar Rp. 600, setelah 4 km pertama
harus membayar Rp. 1.400, dan setiap menempuh 2 km berikutnya harus membayar Rp. 150 dan membayar Rp 100 setelah 1 km. Budi menaiki angkutan kota
tersebut sejauh 21 km, berapakah Budi minimal harus membayar jasa angkutan kota tersebut?
3). Lingkaran dengan pusat A berjari-jari 3 dan lingkaran dengan pusat B berjari-jari 1 seperti pada gambar. Berapakah jarak dari O ke D?

4). Perhatikan gambar di bawah ini! Segitiga ABC sama kaki dengan AB = AC dan BC = 30 cm. persegi EFGH mempunyai panjang sisi 12 cm.
Berapakah luas segitiga AEF?

5). Jika gambar di bawah ini menunjukan lipatan untuk membuat kubus, huruf apakah yang berhadapan dengan huruf G?

6). Dalam bujur sangkar ajaib seperti pada gambar, jumlah angka pada setiap baris, kolom dan diagonal adalah sama. Berapakah jumlah tiga angka
dari sembarang barisnya?

7). Jika panjang sisi persegi ABCD 1 cm, berapakah luas bangun yang diarsir?

8). Jika $x$ dan $y$ dua bilangan positif dan rata-rata dari 4, 20, dan $x$ adalah sama dengan rata-rata dari $y$ dan 16. Berapakah rasio
dari $x$ dan $y$?
9). Jika $ -2 \leq x \leq 5$, $-3 \leq y \leq 5$, $4 \leq z \leq 8$ dan $w=xy-z$, berapakah nilai terkecil dari $w$ yang memenuhi?
10). Suatu daerah dibatasi oleh persamaan $y=2x+2$, $y= \frac{1}{2}x + 1$ dan $y=- \frac{3}{4} x+7$. Berapakah nilai maksimum $y$ pada
daerah tersebut?
Kembali ke Daftar Isi Olimpiade Matik SMP
Kembali ke Solusi Singkat Olim Matik SD-SMP-SMA
Demikian artikel Solusi Singkat Soal OSK 2002 Bagian II Olim SMP ini. Silahkan juga baca materi lain yang berkaitan dengan materi ini. Setiap artikel akan diupdate secara bertahap. Jika ada kritik dan saran, atau koreksi dari isi artikel di halaman ini, mohon bantuannya untuk menuliskannya di kolom komentar di bagian bawah setiap artikel. Ini sangat membantu untuk memperbaiki kualitas dari artikel di blog koma. Semoga bermanfaat. Terimakasih.
Soal-soal Tanpa Solusi
1). Misalkan titik A terletak pada garil L yaitu $y=5x+3$. Koordinat titik B adalah $(3,-2)$. Jika T adalah titik tengah dari AB sehingga AB tegak lurus dengan garis L, tentukan persamaan garis yang sejajar L dan melalui T!
2). Suatu angkutan kota mempunyai aturan pembayaran sebagai berikut. Pada saat naik setiap penumpang harus membayar Rp. 600, setelah 4 km pertama harus membayar Rp. 1.400, dan setiap menempuh 2 km berikutnya harus membayar Rp. 150 dan membayar Rp 100 setelah 1 km. Budi menaiki angkutan kota tersebut sejauh 21 km, berapakah Budi minimal harus membayar jasa angkutan kota tersebut?
3). Lingkaran dengan pusat A berjari-jari 3 dan lingkaran dengan pusat B berjari-jari 1 seperti pada gambar. Berapakah jarak dari O ke D?

4). Perhatikan gambar di bawah ini! Segitiga ABC sama kaki dengan AB = AC dan BC = 30 cm. persegi EFGH mempunyai panjang sisi 12 cm. Berapakah luas segitiga AEF?

5). Jika gambar di bawah ini menunjukan lipatan untuk membuat kubus, huruf apakah yang berhadapan dengan huruf G?

6). Dalam bujur sangkar ajaib seperti pada gambar, jumlah angka pada setiap baris, kolom dan diagonal adalah sama. Berapakah jumlah tiga angka dari sembarang barisnya?

7). Jika panjang sisi persegi ABCD 1 cm, berapakah luas bangun yang diarsir?

8). Jika $x$ dan $y$ dua bilangan positif dan rata-rata dari 4, 20, dan $x$ adalah sama dengan rata-rata dari $y$ dan 16. Berapakah rasio dari $x$ dan $y$?
9). Jika $ -2 \leq x \leq 5$, $-3 \leq y \leq 5$, $4 \leq z \leq 8$ dan $w=xy-z$, berapakah nilai terkecil dari $w$ yang memenuhi?
10). Suatu daerah dibatasi oleh persamaan $y=2x+2$, $y= \frac{1}{2}x + 1$ dan $y=- \frac{3}{4} x+7$. Berapakah nilai maksimum $y$ pada daerah tersebut?
Soal-soal dengan Solusi Singkat
1). Misalkan titik A terletak pada garil L yaitu $y=5x+3$. Koordinat titik B adalah $(3,-2)$. Jika T adalah titik tengah dari AB sehingga AB tegak lurus dengan garis L, tentukan persamaan garis yang sejajar L dan melalui T!





Kembali ke Daftar Isi Olimpiade Matik SMP
Kembali ke Solusi Singkat Olim Matik SD-SMP-SMA
Demikian artikel Solusi Singkat Soal OSK 2002 Bagian II Olim SMP ini. Silahkan juga baca materi lain yang berkaitan dengan materi ini. Setiap artikel akan diupdate secara bertahap. Jika ada kritik dan saran, atau koreksi dari isi artikel di halaman ini, mohon bantuannya untuk menuliskannya di kolom komentar di bagian bawah setiap artikel. Ini sangat membantu untuk memperbaiki kualitas dari artikel di blog koma. Semoga bermanfaat. Terimakasih.