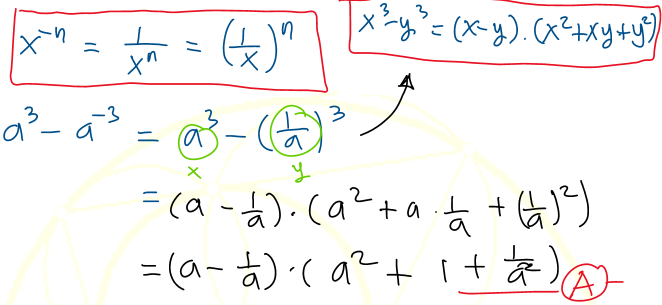Blog Koma - Hallow sahabat koma, bagaimana kabarnya hari ini? Semoga baik-baik saja ya.
Pada artikel ini kita akan membahas Solusi Singkat Soal OSK 2002 Bagian I Olim SMA sebagai pendukung dan menambah wawasan pemahaman
berbagai variasi soal-soal olimpiade matematika tingkat SMA. Dengan berlatih secara rutin dan giat dalam mempelajari
Soal dan Solusi Soal OSK-OSP-OSN Olim Matik SMA yang ada, tentu sahabat koma akan lebih siap dalam menghadapi olimpiade atau kompetisi
matematika yang ada. Semangat terus untuk berlatih. Jika ada masukan atau ide atau cara lain mengenai
Solusi Singkat Soal OSK 2002 Bagian I Olim SMA ini, mohon untuk dishare ke admin ya, biar terus ada perbaikan dan peningkatan
dari isi artikel yang ada di blog koma.
1). Bilangan $\frac{(2^4 )^8}{(4^8 )^2} $ sama dengan ...
A. $\frac{1}{4} $
B. $\frac{1}{2} $
C. 1
D. 2
E. 8
2). Bando selalu berbohong. Suatu hari dia berkata kepada Andi, "Paling tidak salah satu di antara kita tidak pernah berbohong." Maka kita tahu pasti bahwa
A. Andi selalu berhong
B. Andi sesekali berbohong
C. Andi selalu berkata benar
D. Andi sesekali berkata benar
E. Andi tidak pernah berkata apa pun
3). Bilangan n terbesar sehingga $44^{44}$ habis dibagi $8^n$ adalah ...
A. 8
B. 22
C. 29
D. 44
E. 88
4). Pernyataan manakah yang benar?
A. Jika $x < 0$ maka $x^2 > x$
B. Jika $x^2 > 0$ maka $x > 0$
C. Jika $x^2 > x$ maka $x > 0$
D. Jika $x^2 > x$ maka $x < 0$
E. Jika $x < 1$ maka $x^2 < x$
5). Jika $ x^{-n} =\left( \frac{1}{x} \right)^n $ untuk semua bilangan real $x$, maka $a^3 - a^{-3} $ sama dengan ...
A. $\left( a - \frac{1}{a} \right) \left(a^2 + 1 + \frac{1}{a^2} \right) $
B. $\left( \frac{1}{a} - a \right) \left(a^2 - 1 + \frac{1}{a^2} \right) $
C. $\left( a - \frac{1}{a} \right) \left(a^2 - 2 + \frac{1}{a^2} \right) $
D. $\left( \frac{1}{a} - a \right) \left(a^2 + 1 + \frac{1}{a^2} \right) $
E. Pilihan A, B, C, D salah
6). Lima ekor kambing maka rumput yang luasnya 5 kali lapangan bola dalam 5 hari. Berapa hari yang diperlukan 3 ekor kambing untuk makan rumpit yang luasnya 3 kali lapangan bola?
A. 2
B. 3
C. 4
D. 5
E. 6
7). Untuk setiap $x$, $y$ bilangan real, berlaku $x*y=xy-x+y$. Maka $(x+y)*(x-y)$ sama dengan ...
A. $x^2-y^2+2x$
B. $x^2-y^2-2x$
C. $x^2-y^2+2y$
D. $x^2-y^2-2y$
E. $x^2-y^2$
8). Berapa banyak pasangan bilangan asli $(a, b)$ yang memenuhi $ \frac{1}{a} + \frac{1}{b} = \frac{1}{6} $?
A. 1
B. 2
C. 3
D. 4
E. 5
9). Jika garis $y=6x$ memotong $y=x^2+a$ tepat di satu titik, tentukan nilai $a$.
A. 7
B. 8
C. 9
D. 10
E. 11
10). Digit 1, 9, 9, 8 pada bilangan 1998 memiliki jumlah $1+9+9+8=27$. Bilangan berikutnya yang berjumlah digit 27 terjadi di antara tahun ...
A. 2500 dan 2700
B. 2701 dan 2900
C. 2901 dan 3100
D. 3101 dan 9900
E. 9901 dan 9999
1). Bilangan $\frac{(2^4 )^8}{(4^8 )^2} $ sama dengan ...
A. $\frac{1}{4} $
B. $\frac{1}{2} $
C. 1
D. 2
E. 8
2). Bando selalu berbohong. Suatu hari dia berkata kepada Andi, "Paling tidak salah satu di antara kita tidak pernah berbohong." Maka kita
tahu pasti bahwa
A. Andi selalu berhong
B. Andi sesekali berbohong
C. Andi selalu berkata benar
D. Andi sesekali berkata benar
E. Andi tidak pernah berkata apa pun
3). Bilangan n terbesar sehingga $44^{44}$ habis dibagi $8^n$ adalah ...
A. 8
B. 22
C. 29
D. 44
E. 88
4). Pernyataan manakah yang benar?
A. Jika $x < 0$ maka $x^2 > x$
B. Jika $x^2 > 0$ maka $x > 0$
C. Jika $x^2 > x$ maka $x > 0$
D. Jika $x^2 > x$ maka $x < 0$
E. Jika $x < 1$ maka $x^2 < x $
5). Jika $ x^{-n} =\left( \frac{1}{x} \right)^n $ untuk semua bilangan real $x$, maka $a^3 - a^{-3} $ sama dengan ...
A. $\left( a - \frac{1}{a} \right) \left(a^2 + 1 + \frac{1}{a^2} \right) $
B. $\left( \frac{1}{a} - a \right) \left(a^2 - 1 + \frac{1}{a^2} \right) $
C. $\left( a - \frac{1}{a} \right) \left(a^2 - 2 + \frac{1}{a^2} \right) $
D. $\left( \frac{1}{a} - a \right) \left(a^2 + 1 + \frac{1}{a^2} \right) $
E. Pilihan A, B, C, D salah
6). Lima ekor kambing maka rumput yang luasnya 5 kali lapangan bola dalam 5
hari. Berapa hari yang diperlukan 3 ekor kambing untuk makan rumpit yang
luasnya 3 kali lapangan bola?
A. 2
B. 3
C. 4
D. 5
E. 6
7). Untuk setiap $x$, $y$ bilangan real, berlaku $x*y=xy-x+y$.
Maka $(x+y)*(x-y)$ sama dengan ...
A. $x^2-y^2+2x$
B. $x^2-y^2-2x$
C. $x^2-y^2+2y$
D. $x^2-y^2-2y$
E. $x^2-y^2$
8). Berapa banyak pasangan bilangan asli $(a, b)$ yang memenuhi
$ \frac{1}{a} + \frac{1}{b} = \frac{1}{6} $?
A. 1
B. 2
C. 3
D. 4
E. 5
9). Jika garis $y=6x$ memotong $y=x^2+a$ tepat di satu titik, tentukan
nilai $a$.
A. 7
B. 8
C. 9
D. 10
E. 11
10). Digit 1, 9, 9, 8 pada bilangan 1998 memiliki jumlah $1+9+9+8=27$.
Bilangan berikutnya yang berjumlah digit 27 terjadi di antara tahun ...
A. 2500 dan 2700
B. 2701 dan 2900
C. 2901 dan 3100
D. 3101 dan 9900
E. 9901 dan 9999
Kembali ke Daftar Isi Olimpiade Matik SMA
Kembali ke Solusi Singkat Olim Matik SD-SMP-SMA
Demikian artikel Solusi Singkat Soal OSK 2002 Bagian I Olim SMA ini. Silahkan juga baca materi lain yang berkaitan dengan materi ini. Setiap artikel akan diupdate secara bertahap. Jika ada kritik dan saran, atau koreksi dari isi artikel di halaman ini, mohon bantuannya untuk menuliskannya di kolom komentar di bagian bawah setiap artikel. Ini sangat membantu untuk memperbaiki kualitas dari artikel di blog koma. Semoga bermanfaat. Terimakasih.
Soal-soal Tanpa Solusi
1). Bilangan $\frac{(2^4 )^8}{(4^8 )^2} $ sama dengan ...
A. $\frac{1}{4} $
B. $\frac{1}{2} $
C. 1
D. 2
E. 8
2). Bando selalu berbohong. Suatu hari dia berkata kepada Andi, "Paling tidak salah satu di antara kita tidak pernah berbohong." Maka kita tahu pasti bahwa
A. Andi selalu berhong
B. Andi sesekali berbohong
C. Andi selalu berkata benar
D. Andi sesekali berkata benar
E. Andi tidak pernah berkata apa pun
3). Bilangan n terbesar sehingga $44^{44}$ habis dibagi $8^n$ adalah ...
A. 8
B. 22
C. 29
D. 44
E. 88
4). Pernyataan manakah yang benar?
A. Jika $x < 0$ maka $x^2 > x$
B. Jika $x^2 > 0$ maka $x > 0$
C. Jika $x^2 > x$ maka $x > 0$
D. Jika $x^2 > x$ maka $x < 0$
E. Jika $x < 1$ maka $x^2 < x$
5). Jika $ x^{-n} =\left( \frac{1}{x} \right)^n $ untuk semua bilangan real $x$, maka $a^3 - a^{-3} $ sama dengan ...
A. $\left( a - \frac{1}{a} \right) \left(a^2 + 1 + \frac{1}{a^2} \right) $
B. $\left( \frac{1}{a} - a \right) \left(a^2 - 1 + \frac{1}{a^2} \right) $
C. $\left( a - \frac{1}{a} \right) \left(a^2 - 2 + \frac{1}{a^2} \right) $
D. $\left( \frac{1}{a} - a \right) \left(a^2 + 1 + \frac{1}{a^2} \right) $
E. Pilihan A, B, C, D salah
6). Lima ekor kambing maka rumput yang luasnya 5 kali lapangan bola dalam 5 hari. Berapa hari yang diperlukan 3 ekor kambing untuk makan rumpit yang luasnya 3 kali lapangan bola?
A. 2
B. 3
C. 4
D. 5
E. 6
7). Untuk setiap $x$, $y$ bilangan real, berlaku $x*y=xy-x+y$. Maka $(x+y)*(x-y)$ sama dengan ...
A. $x^2-y^2+2x$
B. $x^2-y^2-2x$
C. $x^2-y^2+2y$
D. $x^2-y^2-2y$
E. $x^2-y^2$
8). Berapa banyak pasangan bilangan asli $(a, b)$ yang memenuhi $ \frac{1}{a} + \frac{1}{b} = \frac{1}{6} $?
A. 1
B. 2
C. 3
D. 4
E. 5
9). Jika garis $y=6x$ memotong $y=x^2+a$ tepat di satu titik, tentukan nilai $a$.
A. 7
B. 8
C. 9
D. 10
E. 11
10). Digit 1, 9, 9, 8 pada bilangan 1998 memiliki jumlah $1+9+9+8=27$. Bilangan berikutnya yang berjumlah digit 27 terjadi di antara tahun ...
A. 2500 dan 2700
B. 2701 dan 2900
C. 2901 dan 3100
D. 3101 dan 9900
E. 9901 dan 9999
Soal-soal dengan Solusi Singkat
1). Bilangan $\frac{(2^4 )^8}{(4^8 )^2} $ sama dengan ...
A. $\frac{1}{4} $
B. $\frac{1}{2} $
C. 1
D. 2
E. 8
A. Andi selalu berhong
B. Andi sesekali berbohong
C. Andi selalu berkata benar
D. Andi sesekali berkata benar
E. Andi tidak pernah berkata apa pun
A. 8
B. 22
C. 29
D. 44
E. 88
A. Jika $x < 0$ maka $x^2 > x$
B. Jika $x^2 > 0$ maka $x > 0$
C. Jika $x^2 > x$ maka $x > 0$
D. Jika $x^2 > x$ maka $x < 0$
E. Jika $x < 1$ maka $x^2 < x $
A. $\left( a - \frac{1}{a} \right) \left(a^2 + 1 + \frac{1}{a^2} \right) $
B. $\left( \frac{1}{a} - a \right) \left(a^2 - 1 + \frac{1}{a^2} \right) $
C. $\left( a - \frac{1}{a} \right) \left(a^2 - 2 + \frac{1}{a^2} \right) $
D. $\left( \frac{1}{a} - a \right) \left(a^2 + 1 + \frac{1}{a^2} \right) $
E. Pilihan A, B, C, D salah
A. 2
B. 3
C. 4
D. 5
E. 6
A. $x^2-y^2+2x$
B. $x^2-y^2-2x$
C. $x^2-y^2+2y$
D. $x^2-y^2-2y$
E. $x^2-y^2$
A. 1
B. 2
C. 3
D. 4
E. 5
A. 7
B. 8
C. 9
D. 10
E. 11
A. 2500 dan 2700
B. 2701 dan 2900
C. 2901 dan 3100
D. 3101 dan 9900
E. 9901 dan 9999
Kembali ke Daftar Isi Olimpiade Matik SMA
Kembali ke Solusi Singkat Olim Matik SD-SMP-SMA
Demikian artikel Solusi Singkat Soal OSK 2002 Bagian I Olim SMA ini. Silahkan juga baca materi lain yang berkaitan dengan materi ini. Setiap artikel akan diupdate secara bertahap. Jika ada kritik dan saran, atau koreksi dari isi artikel di halaman ini, mohon bantuannya untuk menuliskannya di kolom komentar di bagian bawah setiap artikel. Ini sangat membantu untuk memperbaiki kualitas dari artikel di blog koma. Semoga bermanfaat. Terimakasih.