Ringkasan Statistika - umptn

         Blog KoMa - Pada artikel ini kita akan membahas materi Ringkasan Statistika - umptn beserta soal-soal yang terkait yang khususnya tentang soal-soal UMPTN baik seleksi bersama ataupun seleksi mandiri seperti SPMB, SNMPTN, SBMPTN, UTBK, UM UGM (utul), simak UI, UM UNDIP, UNPAD, dan lainnya. Untuk melengkapkan materi dan memudahkan pemahaman, kami juga sertakan beberapa contoh soal pendukung (bila diperlukan) untuk menguasai materi Statistika ini. Untuk soal-soal Statistika kita bagi menjadi dua bagian yaitu contoh soal dan soal latihan mandiri. Untuk soal latihan mandiri, teman-teman bisa mencobanya terlebih dahulu, setelah itu baru cek solusinya dibagian bawahnya untuk masing-masing soal latihan mandiri. Kami yakin, dengan tekun belajar maka materi Ringkasan Statistika - umptn ini bisa teman-teman kuasai dengan baik.

Pengertian Statistika

$\clubsuit $ Statistik
       Statistik adalah kumpulan angka atau nilai yang menggambarkan karakteristik suatu kumpulan data.
$\clubsuit $ Statistika
       Statistika adalah ilmu pengetahuan yang berhubungan dengan cara-cara pengumpulan, pengolahan, penyajian dan penafsiran data serta penarikan kesimpulan dari data tersebut.
$\clubsuit $ Datum
       Datum adalah informasi yang diperoleh dari suatu pengamatan dapat berupa angka, lambang atau sifat, dan lainnya.
$\clubsuit $ Data
       Data adalah kumpulan dari informasi atau keterangan yang diperoleh baik dalam bentuk angka dan bukan angka (tulisan), atau data merupakan kumpulan dari datum.
$\clubsuit $ Populasi
       Populasi adalah seluruh objek yang akan diteliti.
$\clubsuit $ Sampel
       Sampel adalah bagian dari populasi yang benar-benar diamati.

       Untuk penjelasan lebih mendetail tentang pengertian Statistika dan jenis-jenis data (ada data tunggal dan data berkelompok), silahkan teman-teman kunjungi link berikut:
Statistika secara umum.

Penyajian Data

       Data-data yang terkumpul dapat disajikan dalam beberapa bentuk seperti tabel, diagram, dan lainnya.

       Untuk keterangan detail tentang penyajian data, silahkan kunjungi link berikut ya:
Penyajian Data.

contoh soal umptn:

1). Soal SBMPTN 2013 MatDas 326
Distribusi berat bayi lahir di rumah sakit A dan B dapat dilihat pada diagram berikut,

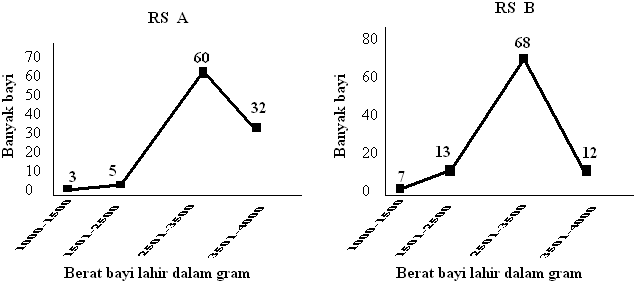
Berat badan bayi dikatakan normal apabila berat lahirnya lebih dari 2500 gram. Banyak bayi normal yang lahir di dua rumah sakit tersebut adalah ...
A). 12
B). 32
C). 44
D). 128
E). 172

$\spadesuit $ Jawaban : E
$\clubsuit $ Pembahasan :
$\spadesuit \, $ Menghitung banyak bayi normal setiap rumah sakit :
RS A = 60 + 32 = 92
RS B = 68 + 12 = 80
$\spadesuit \, $ Sehingga total bayi normal :
Total = RS A + RS B = 92 + 80 = 172 bayi.
Jadi, banyak bayi normal ada 172 bayi. $\heartsuit$

2). Soal SNMPTN 2012 MatDas 122
Jika diagram batang di bawah ini memperlihatkan frekuensi kumulatif hasil tes matematika siswa kelas XII, maka persentase siswa yang memperoleh nilai 8 adalah ...

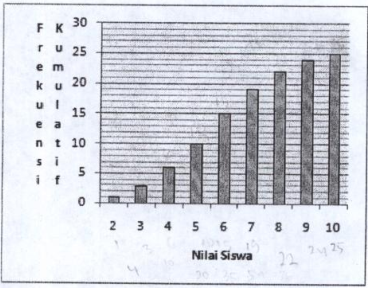
A). 12%
B). 15%
C). 20%
D). 22%
E). 80%

$\spadesuit $ Jawaban : A
$\clubsuit $ Pembahasan :
$\clubsuit \, $ Frekuensi kumulatif siswa yang memperoleh nilai 8 adalah 22 siswa , artinya jumlah siswa yang memperoleh nilai 2 sampai 8 ada 22 siswa, jadi bukan hanya yang mendapat nilai 8 saja.
$\clubsuit \, $ Frekuensi kumulatif siswa yang memperoleh nilai 7 adalah 19 siswa , artinya jumlah siswa yang memperoleh nilai 2 sampai 7 ada 19 siswa, jadi bukan hanya yang mendapat nilai 7 saja.
Sehingga banyak siswa yang mendapat nilia 8 saja = 22 - 19 = 3.
Total siswa ada 25 siswa.
$\clubsuit \, $ Menentukan nilai persentase :
$\begin{align} \text{Persentase nilai 8} \, & = \frac{\text{banyak siswa yang memperoleh nilai 8}}{\text{total siswa}} \times 100\% \\ & = \frac{3}{25} \times 100\% \\ & = 12 \% \end{align} $
Jadi, persentasenya adalah $ 12 \% . \heartsuit$

Rumus-rumus Data Tunggal

       Untuk lebih mendetail mengenai rumus-rumus penghitungan pada statistika, silahkan sahabat koma kunjungi link berikut:
1). Ukuran Pemusatan
2). Ukuran Letak
3). Ukuran Penyebaran

contoh soal umptn:

3). Soal SPMB 2007 MatDas
Jika data $2,a,a,3,4,6 $ mempunyai rataan $c $ . Dan data $2,c,c,4,6,2,1 $ mempunyai rataan $2a$ , maka nilai $c$ adalah ....
A). 3
B). 2,5
C). 2
D). 1,5
E). 1

$\spadesuit $ Jawaban : A
$\clubsuit $ Pembahasan :
$\clubsuit \,$ Rataan pertama
$\begin{align} \frac{2+a+a+3+4+6}{6} & = c \\ 2a + 15 & = 6c \\ 2a - 6c & = -15 \, \, \, \text{...pers(i)} \end{align}$
$\clubsuit \,$ Rataan kedua
$\begin{align} \frac{2+c+c+4+6+2+1}{7} & = 2a \\ 2c + 15 & = 14a \\ 14a - 2c & = 15 \, \, \, \text{...pers(ii)} \end{align}$
$\clubsuit \,$ Eliminasi pers(i) dan pers(ii)
$\begin{array}{c|c|cc} 2a - 6c = -15 & \times 7 & 14a - 42c = -105 & \\ 14a - 2c = 15 & \times 1 & 14a - 2c = 15 & - \\ \hline & & -40c = -120 \rightarrow c=3 & \end{array} $
Jadi, nilai $ c=3. \heartsuit $

4). Soal SNMPTN 2012 MatDas 122
Budi telah mengikuti empat kali tes matematika pada semester I dengan nilai rata-rata 7,0. Jika selama setahun Budi mngikuti delapan kali tes dengan nilai rata-rata 8,0 , maka nilai rata-rata pada semester II dibandingkan dengan semester I naik sebesar ...
A). 1,0
B). 1,2
C). 1,5
D). 1,8
E). 2,0

$\spadesuit $ Jawaban : E
$\clubsuit $ Pembahasan :
$\spadesuit \, $ Permisalan :
rata-rata semester I : $\overline{x}_1 = 7 \, $ , banyak tes semester I : $n_1 = 4 $
rata-rata semester II : $\overline{x}_2 = a \, $ , banyak tes semester II : $n_2 = 8 - 4 = 4 $
rata-rata gabungannya : $\overline{x}_{\text{gb}} = 8$
$\spadesuit \, $ Rumus rata-rata gabungan : $ \overline{x}_{\text{gb}} = \frac{n_1.\overline{x}_1 + n_2.\overline{x}_2}{n_1 + n_2}$
$\begin{align*} \overline{x}_{\text{gb}} & = \frac{n_1.\overline{x}_1 + n_2.\overline{x}_2}{n_1 + n_2} \\ 8 & = \frac{4.7 + 4.a}{4 + 4} \\ 8 & = \frac{28 + 4a}{8} \\ 8.8 & = 28 + 4a \\ 4a & = 64 - 28 \\ 4a & = 36 \\ a & = \frac{36}{4} = 9 \end{align*}$
artinya nilai rata-rata semester II = 9.
sehingga kenaikkan nilai dari semester I ke semester II sebesar 9 - 7 = 2.
Jadi, nilai rata-rata pada semester II dibandingkan dengan semester I naik sebesar 2,0 . $\heartsuit$

5). Soal SBMPTN 2013 MatDas 228
Banyak siswa kelas XI A suatu sekolah adalah $ m \, $ siswa. Mereka mengikuti tes matematika dengan hasil sebagai berikut. Lima siswa memperoleh skor 90, siswa yang lain memperoleh skor minimal 60, dan rata-rata skor semua siswa adalah 70. Nilai $ m \, $ terkecil adalah ....
A). 16
B). 15
C). 14
D). 13
E). 12

$\spadesuit $ Jawaban : B
$\clubsuit $ Pembahasan :
$\clubsuit \, $ Konsep rata-rata gabungan : $ \overline{X}_\text{gb} = \frac{n_1.\overline{X}_1 + n_2.\overline{X}_2}{n_1+n_2} $
Keterangan :
$ n_1 \, $ = banyak kelomok pertama, $ \overline{X}_1 \, $ = rata - rata kelompok pertama,
dan $ \overline{X}_\text{gb} \, $ = rata-rata gabungan semua kelompok.
dari soal diketahui :
$ n_1 = 5, \, \overline{X}_1 = 90, \, n_2 = (m-5) , \, \overline{X}_2 \text{(min)} = 60, \, \overline{X}_\text{gb} = 70 $
$\clubsuit \, $ Menentukan nilai $ m $
Karena yang dipilih rata-rata kelompok dua ($\overline{X}_2$) adalah rata-rata minimal, maka rata-rata gabungan aslinya lebih besar dari rata-rata gabungan minimalnya.
$\begin{align} \overline{X}_\text{gb} & \geq \overline{X}_\text{gb} \text{(minimal)} \\ \overline{X}_\text{gb} & \geq \frac{n_1.\overline{X}_1 + n_2.\overline{X}_2 \text{(minimal)}}{n_1+n_2} \\ 70 & \geq \frac{5.90 + (m-5).60 }{5 + (m-5)} \\ 70 & \geq \frac{450 + 60m-300 }{m} \\ 70m & \geq 60m + 150 \\ 10 m & \geq 150 \\ m & \geq 15 \end{align}$
karena nilai $ m \geq 15 \, $ , maka nilai $ m \, $ terkecilnya adalah $ m = 15 $ .
Jadi, nilai $ m \, $ terkecil adalah $ m = 15. \heartsuit $

6). Soal SPMB 2004 MatDas
Nilai rata-rata tes matematika dari kelompok siswa dan kelompok siswi di suatu kelas berturut-turut adalah 5 dan 7. Jika nilai rata-rata di kelas tersebut adalah 6,2 , maka perbandingan banyaknya siswa dan siswi adalah ....
A). 2 : 3
B). 3 : 4
C). 2 : 5
D). 3 : 5
E). 4 : 5

$\spadesuit $ Jawaban : A
$\clubsuit $ Pembahasan :
Cara I:
$\spadesuit \, $ Data dibagi menjadi dua kelompok
banyak siswa = $n_a \, $ , rata - rata siswa : $ \overline{x}_a = 5 $
banyak siswi = $n_i \, $ , rata - rata siswi : $ \overline{x}_i = 7 $
rata - rata gabungan : $\overline{x}_{gb} = 6,2 $
$\spadesuit \, $ Menentukan perbandingan dengan rata - rata gabungan
$\begin{align} \overline{x}_{gb} & = \frac{n_a. \overline{x}_a + n_i.\overline{x}_i}{n_a + n_i} \\ 6,2 & = \frac{5n_a + 7n_i}{n_a + n_i} \\ 6,2n_a+6,2n_i & = 5n_a + 7n_i \\ 6,2n_a-5n_a & = 7n_i - 6,2n_i \\ 1,2n_a & = 0,8n_i \\ \frac{n_a}{n_i} & = \frac{0,8}{1,2} = \frac{8}{12} = \frac{2}{3} \end{align}$
Jadi, perbandingan banyaknya siswa dan siswi adalah 2 : 3 $ \heartsuit $

Cara II:
$\spadesuit \, $ Data dibagi menjadi dua kelompok
banyak siswa = $n_a \, $ , rata - rata siswa : $ \overline{x}_a = 5 $
banyak siswi = $n_i \, $ , rata - rata siswi : $ \overline{x}_i = 7 $
rata - rata gabungan : $\overline{x}_{gb} = 6,2 $
$\spadesuit \, $ Menentukan perbandingan
$\begin{align} \frac{n_a}{n_i} & = \left| \frac{\overline{x}_{gb} - \overline{x}_i}{\overline{x}_{gb} - \overline{x}_a} \right| \\ & = \left| \frac{6,2 - 7}{6,2 - 5} \right| \\ & = \frac{0,8}{1,2} = \frac{8}{12} = \frac{2}{3} \end{align}$
Jadi, perbandingan banyaknya siswa dan siswi adalah 2 : 3 $ \heartsuit $

7). Soal SPMB 2005 MatDas
Nilai rata-rata ulangan kelas A adalah $\overline{X}_A \, \, $ dan kelas B adalah $\overline{X}_B $ . Setelah kedua kelas digabung, nilai rata-ratanya adalah $\overline{X} $ . Jika $\overline{X}_A : \overline{X}_B = 10 : 9 \, \, $ dan $\overline{X} : \overline{X}_B = 85:81 \, \, $ maka perbandingan banyaknya siswa dikelas A dan B adalah ....
A). 8 : 9
B). 4 : 5
C). 3 : 4
D). 3 : 5
E). 9 : 10

$\spadesuit $ Jawaban : B
$\clubsuit $ Pembahasan :
$\spadesuit \, $ Mengubah persamaan
$\frac{\overline{x}_A}{\overline{x}_B} = \frac{10}{9} \rightarrow \overline{x}_A = \frac{10}{9}\overline{x}_B $
$\frac{\overline{x}}{\overline{x}_B} = \frac{85}{81} \rightarrow \overline{x} = \frac{85}{81}\overline{x}_B = \overline{x}_{gb} $
$\spadesuit \, $ Menentukan perbandingan dengan rata-rata gabungan
$\begin{align} \overline{x}_{gb} & = \frac{n_A.\overline{x}_A+n_B.\overline{x}_B}{n_A+n_B} \\ \frac{85}{81}\overline{x}_B & = \frac{n_A. \frac{10}{9}\overline{x}_B +n_B.\overline{x}_B}{n_A+n_B} \, \, \, \text{(coret } \, \overline{x}_B ) \\ \frac{85}{81} & = \frac{n_A. \frac{10}{9} +n_B}{n_A+n_B} \\ \frac{85}{81}n_A + \frac{85}{81}n_B & = \frac{10}{9}n_A + n_B \\ \frac{85}{81}n_B - n_B & = \frac{10}{9}n_A - \frac{85}{81}n_A \\ \frac{4}{81}n_B & = \frac{5}{81}n_A \, \, \, \text{(coret 81)} \\ 4n_B & = 5n_A \\ \frac{n_A}{n_B} & = \frac{4}{5} \end{align}$
Jadi, perbandingan siswa kelas A dan Kelas B adalah 4 : 5. $ \heartsuit $

8). Soal UTBK 2019 Saintek
Diketahui bilangan $ a, b, 5, 3, 7, 6, 6, 6, 6, 6 $ dengan rata-rata 5 dan variansinya $ \frac{13}{5} $. Nilai $ ab = .... $
A). $ 2 \, $
B). $ 4 \, $
C). $ 6 \, $
D). $ 8 \, $
E). $ 10 $

$\spadesuit $ Jawaban : C
$\clubsuit $ Pembahasan :
*). Rata-rata = 5:
$ \begin{align} \frac{a+b+5+3+7+6+6+6+6+6}{10} & = 5 \\ \frac{a+b+45}{10} & = 5 \\ a+b+45 & = 50 \\ a+b & = 5 \, \, \, \, \, \text{...pers(i)} \end{align} $
*). Variansi = $ \frac{13}{5} $ :
$ \begin{align} \frac{(x_1 - \overline{x})^2 +(x_2 - \overline{x})^2 + ... +(x_{10} - \overline{x})^2 }{10} & = \frac{13}{5} \\ \frac{(a-5)^2 +(b-5)^2 +...+5 \times (6-5)^2}{10} & = \frac{13}{5} \\ \frac{(a-5)^2 +(b-5)^2 +0+4+4 +5 \times 1 }{10} & = \frac{13}{5} \\ (a-5)^2 +(b-5)^2 +13 & = \frac{13}{5} \times 10 \\ (a-5)^2 +(b-5)^2 +13 & = 26 \\ (a-5)^2 +(b-5)^2 & = 13 \\ a^2 - 10a + 25 + b^2 - 10b + 25 & = 13 \\ a^2 + b^2 - 10(a+b) + 50 & = 13 \\ a^2 + b^2 - 10(5) + 50 & = 13 \\ a^2 + b^2 - 50 + 50 & = 13 \\ a^2 + b^2 & = 13 \end{align} $
*). Menentukan nilai $ ab$ :
$ \begin{align} (a+b)^2 & = a^2 + b^2 + 2ab \\ (5)^2 & = 13 + 2ab \\ 25 & = 13 + 2ab \\ 12 & = 2ab \\ ab & = 6 \end{align} $
Jjadi, nilai $ ab = 6. \heartsuit $

9). Soal SBMPTN 2013 MatDas 326
Median dan rata-rata dari data yang terdiri dari empat bilangan asli yang telah diurutkan mulai dari yang terkeciladalah 8. Jika selisih antara data terbesar dan terkecilnya adalah 10 dan modusnya tunggal, maka hasil kali data kedua dan keempat adalah ...
A). 65
B). 78
C). 91
D). 104
E). 117

$\spadesuit $ Jawaban : D
$\clubsuit $ Pembahasan :
$\clubsuit \, $ Misalkan datanya : $a, \, b, \, c, \, d$
$\clubsuit \, $ Median = 8, $\Rightarrow \frac{b+c}{2}=8 \Rightarrow b+c=16 .$
karena modusnya tunggal, maka haruslah nilai $b=c=8$
$\clubsuit \, $ Rata-rata = 8, $\Rightarrow \frac{a+b+c+d}{4}=8 \Rightarrow a+d + 16=32 .$
$a+d=16 $ ...pers(i)
$\clubsuit \, $ Selisih data terbesar dan terkecilnya (jangkauannya) 10 .
$d-a = 10$ ...pers(ii)
$\clubsuit \, $ Eliminasi pers(i) dan per(ii) diperoleh $a=3 \, $ dan $d=13$ .
datanya menjadi : 3, 8, 8, 13
sehingga hasil kali data kedua dan keempat = 8 $\times$ 13 = 104
Jadi, hasil kali data kedua dan keempat adalah 104. $\heartsuit $

10). Soal SNMPTN 2009 MatDas 283
Rata-rata sekelompok bilangan adalah 40. Ada bilangan yang sebenarnya adalah 60, tetapi terbaca 30. Setelah dihitung kembali, ternyata rata-rata yang benar adalah 41. Banyak bilangan dalam kelompok itu adalah ...
A). 20
B). 25
C). 30
D). 42
E). 45

$\spadesuit $ Jawaban : C
$\clubsuit $ Pembahasan :
Cara I:
$\clubsuit \, $ Permisalan :
Banyak bilangan ada $n$ bilangan dan total jumlah ($n-1$) bilangan ($x_1+x_2+...+x_{(n-1)} = A $ ) adalah $A$
penyelesaian dibagi menjadi dua kasus :
$\clubsuit \, $ Kasus salah
nilai salah = 30 dan rata-rata salah = 40 .
$\overline{x} = \frac{\text{Jumlah total nilai}}{\text{banyak bilangan}} \rightarrow 40 = \frac{A+30}{n} \rightarrow 40n=A+30$ ...pers(i)
$\clubsuit \, $ Kasus benar
nilai benar = 60 dan rata-rata benar = 41 .
$\overline{x} = \frac{\text{Jumlah total nilai}}{\text{banyak bilangan}} \rightarrow 41 = \frac{A+60}{n} \rightarrow 41n=A+60$ ...pers(ii)
$\clubsuit \, $ Eliminasi pers(i) dan pers(ii)
$\begin{array}{cc} 41n=A+60 & \\ 40n=A+30 & - \\ \hline n = 30 & \end{array}$
Jadi, banyak bilangan ada 30 bilangan. $\heartsuit $

Cara II:
$\clubsuit \, $ Untuk kasus seperti ini, berlaku rumus :
$n=\frac{x_b-x_s}{\overline{x_b}-\overline{x_s}} \, $ atau $ \, n=\frac{x_s-x_b}{\overline{x_s}-\overline{x_b}} $
Jika hasilnya negatif, beri tanda mutlak agar hasilnya selalu positif.
Keterangan :
$n \rightarrow $ banyak bilangan atau orang (data)
$\overline{x_b} \rightarrow $ rata-rata benar
$\overline{x_s} \rightarrow $ rata-rata salah
$x_b \rightarrow $ nilai benar
$x_s \rightarrow $ nilai salah
$\clubsuit \, $ Menentukan banyak bilangan
$n=\frac{x_b-x_s}{\overline{x_b}-\overline{x_s}} = \frac{60-30}{41-40} = \frac{30}{1}=30$
Jadi, banyak bilangan ada 30 bilangan. $\heartsuit $

11). Soal SBMPTN 2015 MatDas 620
Diketahui median dari 11 nilai pengamatan adalah 10, sedangkan rata-rata dari nilai pengamatan yang lebih kecil daripada median adalah 4. Jika rata-rata dari 11 nilai pengamatan tersebut sama dengan dua kali media, maka rata-rata nilai pengamatan yang lebih besar daripada median adalah ...
A). 20
B). 28
C). 38
D). 40
E). 44

$\spadesuit $ Jawaban : C
$\clubsuit $ Pembahasan :
$\clubsuit \,$ Konsep rata-rata gabungan $(\overline{X}_{gb}) $
$ \begin{align} \overline{X}_{gb} = \frac{n_1\overline{X}_1 + n_2\overline{X}_2 + n_3\overline{X}_3}{n_1 + n_2 + n_3} \end{align} $
Keterangan :
$ \overline{X}_{gb} = \, $ rata - rata gabungan
$ \overline{X}_{1} = \, $ rata - rata kelompok I
$ n_1 = \, $ banyak anggota kelompok I
$\clubsuit \, $ Data dibagi menjadi tiga kelompok
*). Kelompok I : data sebelum median ada 5 data dengan rata-rata 4, artinya $ n_1 = 5 \, $ dan $ \overline{X}_1 = 4 $
*). Kelompok II : mediannya itu sendiri, ada 1 data dengan nilai 10, artinya $ n_2 = 1 \, $ dan $ \overline{X}_2 = 10 $
*). Kelompok III : data setelah median ada 5 data dengan rata-rata misalkan $ a $ , artinya $ n_3 = 5 \, $ dan $ \overline{X}_3 = a $
*). rata-rata gabungan = dua kali median
$ \overline{X}_{gb} = 2 \times 10 = 20 $
$\clubsuit \,$ Menentukan nilai $ a $
$\begin{align} \overline{X}_{gb} & = \frac{n_1\overline{X}_1 + n_2\overline{X}_2 + n_3\overline{X}_3}{n_1 + n_2 + n_3} \\ 20 & = \frac{5.4 + 1.10 + 5.a}{5 + 1 + 5} \\ 20 & = \frac{20 + 10 + 5a}{11} \\ 220 & = 30 + 5a \\ 5a & = 190 \\ a & = 38 \end{align} $
Jadi, rata-rata nilai pengamatan lebih besar daripada median adalah 38. $ \heartsuit $

12). Soal SBMPTN 2015 MatDas 622
Nilai semua tes matematika dinyatakan dengan bilangan bulat dari 0 sampai 10. Media terkecil yang mungkin bagi siswa yang memiliki rata-rata nilai 6 dari enam kali tes adalah ...
A). 3
B). 4
C). 5
D). 6
E). 7

$\spadesuit $ Jawaban : B
$\clubsuit $ Pembahasan :
$\clubsuit \,$ Konsep rata-rata : $ \overline{X} = \frac{\text{Jumlah semua data}}{\text{banyak data}} $
$\clubsuit \, $ Misalkan datanya : $ x_1, x_2, x_3, x_4, x_5 x_6 \, $ yang telah diurutkan dari kecil ke besar dengan rata-ratanya 6, sehingga diperoleh :
$\begin{align} \overline{X} & = 6 \\ \frac{x_1+x_2+x_3+x_4+x_5+x_6}{6} & = 6 \\ x_1+x_2+x_3+x_4+x_5+x_6 & = 36 \, \, \, \, \text{ ...pers(i)} \end{align} $
Sementara nilai mediannya : $ Me = \frac{x_3+x_4}{2} $
$\clubsuit \,$ Analisa nilai data yang mungkin
*). Agar mediannya sekecil mungkin, maka nilai $ x_3 \, $ dan $ x_4 \, $ juga harus terkecil.
*). Agar $ x_3 \, $ dan $ x_4 \, $ terkecil, maka nilai $ x_5 \, $ dan $ x_6 \, $ harus terbesar, dengan nilai $ x_5 = 10 \, $ dan $ x_6 = 10. $
$\begin{align} x_1+x_2+x_3+x_4+x_5+x_6 & = 36 \\ x_1+x_2+x_3+x_4+10+10 & = 36 \\ x_1+x_2+x_3+x_4& = 16 \, \, \, \, \text{ ...pers(ii)} \end{align} $
*). karena nilai $ x_1 \leq x_2 \leq x_3 \leq x_4 , \, $ maka dari pers(ii) diperoleh nilai $ x_1 = 4, x_2=4, x_3=4,x_4=4 \, \, \, $ yang menyebabkan nilai $ x_3 \, $ dan $ x_4 \, $ terkecil.
Sehingga : $ Me = \frac{x_3+x_4}{2} = \frac{4+4}{2} = 4 $
Jadi, nilai median terkecilnya adalah 4. $ \heartsuit $

13). Soal UM UGM 2016 MatDas 571
Nilai rata-rata Bahasa Inggris dalam suatu kelas yang terdiri dari 14 siswa adalah 6. Satu siswa memperoleh nilai tertinggi dan satu siswa lain memperoleh nilai terendah. Nilai rata-rata tanpa nilai tertinggi dan terendah juga sama dengan 6. Jika nilai terendahnya adalah $ b \, $ , maka selisih nilai tertinggi dan terendah adalah ....
A). $ 10 - b \, $
B). $ 12 - 2b \, $
C). $ 18-3b \, $
D). $ 20-4b \, $
E). $ 3b-4 $

$\spadesuit $ Jawaban : B
$\clubsuit $ Pembahasan :
*). Misalkan nilai tertinggi seorang siswa adalah sebesar $ y $. Di soal juga sudah diketahui nilai terendah seorang siswa adalah sebesar $ b $. Sedangkan jumlah semua nilai selain tertinggi dan terendah kita misalkan sebesar N (total nilai untuk 12 orang dari 14 orang selain siswa dengan nilai tertinggi dan terendah).
*). Rata-rata 14 siswa adalah 6
$\begin{align} \text{Rata-rata 14 siswa } & = 6 \\ \frac{\text{jumlah semua data/nilai}}{\text{banyak data/nilai}} & = 6 \\ \frac{b + N + y}{14} & = 6 \\ b + N + y & = 6 \times 14 \\ b + N + y & = 84 \, \, \, \, \, \text{...(i)} \end{align} $
*). Rata-rata 12 siswa (siswa nilai tertinggi dan terendah tidak diikutkan) adalah 6
$\begin{align} \text{Rata-rata 12 siswa } & = 6 \\ \frac{\text{jumlah semua data/nilai}}{\text{banyak data/nilai}} & = 6 \\ \frac{N}{12} & = 6 \\ N & = 6 \times 12 \\ N & = 72 \, \, \, \, \, \text{...(ii)} \end{align} $
*). Substitusi nilai $ N = 72 \,$ ke pers(i) :
$ b + N + y = 84 \rightarrow b + 72 + y = 84 \rightarrow y = 12 - b $
Artinya kita peroleh nilai tertinggi $(y)$ yaitu $ y = 12 - b $.
*). Menentukan nilai selisih tertinggi ($y$) dan terendah ($b$) :
$ y - b = (12-b) - b = 12 - 2b $.
Jadi, selisih nilai tertinggi dan terendahnya adalah $ 12 - 2b . \, \heartsuit $

14). Soal SBMPTN 2016 MatDas 348
Nilai ujian matematika 40 siswa pada suatu kelas berupa bilangan cacah tidak lebih daripada 10. Rata-rata nilai mereka adalah 7 dan hanya terdapat 10 siswa yang memperoleh nilai 6. Jika $ q $ menyatakan banyak siswa yang memperoleh nilai kurang dari 5, maka nilai $ q $ terbesar yang mungkin adalah ....
A). $ 11 \, $
B). $ 12 \, $
C). $ 13 \, $
D). $ 15 \, $
E). $ 17 $

$\spadesuit $ Jawaban : C
$\clubsuit $ Pembahasan :
*). Rata-rata nilai 40 siswa adalah 7 dan hanya terdapat 10 siswa yang memperoleh nilai 6. Misalkan jumlah nilai 30 siswa yang selain mendapat nilai 6 adalah $ A_{30} $, maka kita peroleh :
$ \begin{align} \text{rata-rata} & = 7 \\ \frac{\text{jumlah semua nilai}}{\text{banyak nilai}} & = 7 \\ \frac{A_{30} + 10 \times 6}{40} & = 7 \\ A_{30} + 60 & = 280 \\ A_{30} & = 220 \end{align} $
Artinya jumlah nilai keseluruhan 30 orang adalah 220.
*). $ q $ menyatakan banyak siswa yang memperoleh nilai kurang dari 5. Nilai $ q $ terbesar yang mungkin dengan nilai ujian tidak lebih dari 10 yaitu :
-). Untuk $ q = 15 \rightarrow $ jumlah terbesar nilai kurang dari 5 adalah $ 15 \times 4 = 60 $ , sehingga sisa $ = 220 - 60 = 160 $.
Sementara jumlah terbesar nilai > 6 adalah $ 15 \times 10 = 150 $ yang belum mencapai 160 sehingga tidak mungkin $ q = 15 $.
-). Untuk $ q = 14 \rightarrow $ jumlah terbesar nilai kurang dari 5 adalah $ 14 \times 4 = 56 $ , sehingga sisa $ = 220 - 56 = 164 $.
Sementara jumlah terbesar nilai > 6 adalah $ 16 \times 10 = 160 $ yang belum mencapai 164 sehingga tidak mungkin $ q = 14 $.
-). Untuk $ q = 13 \rightarrow $ jumlah terbesar nilai kurang dari 5 adalah $ 13 \times 4 = 52 $ , sehingga sisa $ = 220 - 52 = 168 $.
Sementara jumlah terbesar nilai > 6 adalah $ 17 \times 10 = 170 $ yang mencapai 168 sehingga nilai $ q = 13 $ memenuhi dengan perincian 13 siswa memiliki nilai kurang dari 5 , 1 siswa dengan nilai 8 dan 16 siswa memiliki nilai 10.
Jadi, nilai terbesar $ q $ adalah $ q = 13 . \, \heartsuit $

15). Soal SBMPTN 2017 MatDas 224
Diketahui median dan rata-rata berat badan 5 balita adalah sama. Setelah ditambahkan satu data berat badan balita, rata-ratanya meningkat 1 kg, sedangkan mediannya tetap. Jika 6 data berat badan tersebut diurutkan dari yang paling ringan ke yang paling berat, maka selisih berat badan antara balita terakhir yang ditambahkan dan balita diurutan ke-4 adalah .... kg.
A). $ 4 \, $
B). $ \frac{9}{2} \, $
C). $ 5 \, $
D). $ 6 \, $
E). $ \frac{13}{2} \, $

$\spadesuit $ Jawaban : D
$\clubsuit $ Pembahasan :
Cara I:
*). Data awal : $ a, b, c, d, e $
(Sudah diurutkan dari ringan ke berat).
Median $ = c $ dan rata-rata $ = \frac{a+b+c+d+e}{5} $.
$\begin{align} \text{rata-rata } & = \text{ median } \\ \frac{a+b+c+d+e}{5} & = c \\ a+b+c+d+e & = 5 c \, \, \, \, \, \, \text{....(i)} \end{align} $

*). Data baru dengan menambahkan $ x $, ada beberapa kemungkinan letak $ x $ yaitu :
a). Kemungkinan I : $ a, b, x, c, d,e $ atau $ a,b,c,x,d,e$
Karena median tetap yaitu $ c $ maka
median $ = c \rightarrow \frac{x+c}{2} = c \rightarrow x = c $.
Rata-rata $ = \frac{(a+b+c+d+e)+x}{6} = \frac{5c + c}{6} c $
(rata-rata tidak meningkat) sehingga kemungkinan I tidak berlaku.

b). Kemungkinan II : $ x,a,b,c,d,e $ atau $ a,x,b,c,d,e$
data keempat adalah $ c $.
-). rata-rata meningkat 1 kg.
$\begin{align} \text{rata-rata } & = c + 1 \\ \frac{a+b+c+d+e+x}{6} & = c + 1 \\ (a+b+c+d+e)+x & = 6c + 6 \\ 5c+x & = 6c + 6 \\ x & = c + 6 \end{align} $
Dari bentuk $ x = c + 6 $ seharusnya nilai $ c $ lebih kecil dari $ x $, akan tetapi pada kemungkinan II ini sebaliknya, sehingga kemungkinan II tidak berlaku.
c). Kemungkinan III : $ a,b,c,d,x,e $ atau $ a,b,c,d,e,x$
data keempat adalah $ d $.
-). Median tetap :
Median $ = c \rightarrow \frac{c+d}{2} = c \rightarrow c = d $
-). rata-rata meningkat 1 kg.
$\begin{align} \text{rata-rata } & = c + 1 \\ \frac{a+b+c+d+e+x}{6} & = c + 1 \\ (a+b+c+d+e)+x & = 6c + 6 \\ 5c+x & = 6c + 6 \\ x & = c + 6 \, \, \, \, \, \, ( c \leq x \, \text{Benar)} \\ x - c & = 6 \, \, \, \, \, \, \text{(dari } c = d ) \\ x - d & = 6 \end{align} $
Sehingga selisihnya adalah 6.
Jadi, selisihnya adalah $ 6 . \, \heartsuit $

Cara II:
*). Data awal : $ a, b, c, d, e $
(Sudah diurutkan dari ringan ke berat).
Median $ = c $ dan rata-rata $ = \frac{a+b+c+d+e}{5} $.
$\begin{align} \text{rata-rata } & = \text{ median } \\ \frac{a+b+c+d+e}{5} & = c \\ a+b+c+d+e & = 5 c \, \, \, \, \, \, \text{....(i)} \end{align} $

*). Data baru dengan menambahkan $ x $, sehingga sekarang ada 6 nilai denga rata-rata meningkat 1 kg.
$\begin{align} \text{rata-rata } & = c + 1 \\ \frac{a+b+c+d+e+x}{6} & = c + 1 \\ (a+b+c+d+e)+x & = 6c + 6 \\ 5c+x & = 6c + 6 \\ x & = c + 6 \, \, \, \, \, \, \text{....(ii)} \end{align} $
Dari bentuk $ x = c + 6 $ seharusnya nilai $ c $ lebih kecil dari $ x $ dan $ x \neq c $, artinya ada dua kemungkinan yaitu $ a,b,c,d,x,e $ atau $ a,b,c,d,e,x$ dengan data keempat adalah $ d $.
*). Median tetap :
Median $ = c \rightarrow \frac{c+d}{2} = c \rightarrow c = d $
*). Substitusi $ c = d $ ke pers(ii) :
$ x = c + 6 \rightarrow x = d + 6 \rightarrow x - d = 6 $.
Sehingga selisihnya adalah 6.
Jadi, selisihnya adalah $ 6 . \, \heartsuit $

16). Soal UM UGM 2017 MatDas 723
Suatu desa berpenduduk 5000 jiwa, terdiri atas kelompok berpendidikan terakhir SD, SMP, SMA, dan Perguruan TInggi (PT). Perbandingan jumlah penduduk berpendidikan terakhir SD, SMP, dan SMA sebesar $ 2 : 6 : 4 $. Jika persentase penduduk berpendidikan PT sebesar 4% dari total penduduk desa, maka jumlah penduduk berpendidikan terakhir SD sebesar ....
A). $ 2400 $
B). $ 2000 $
C). $ 1600 $
D). $ 1000 $
E). $ 800 $

$\spadesuit $ Jawaban : E
$\clubsuit $ Pembahasan :
*). Diketahui pada soal :
-). SD : SMP : SMA = 2 : 6 : 4
-). PT = 4% dari keseluruhan penduduk, sehingga sisanya 96% adalah penduduk berpendidikan $ \text{SD + SMP + SMA} $.
*). Menentukan persentase SD :
Dari nilai perbandingan,
$\begin{align} \frac{\text{%SD}}{\text{%(SD + SMP + SMA)}} & = \frac{2}{2 + 6 + 4} \\ \frac{\text{%SD}}{96\%} & = \frac{2}{12} \\ \text{%SD} & = \frac{2}{12} \times 96\% \\ \text{%SD} & = 16\% \end{align} $
Artinya banyak SD adalah 16% dari keseluruhan penduduk.
*). Menentukan penduduk berpendidikan SD :
$\begin{align} \text{ Banyak SD } & = 16\% \times \text{ keseluruhan} \\ & = \frac{16}{100} \times 5000 \\ & = 800 \end{align} $
Jadi, jumlah penduduk berpendidikan terakhir SD ada $ 800 . \, \heartsuit $

17). Soal SBMPTN 2018 MatDas 526
Sebelas siswa mengikuti suatu tes dan median nilai tes mereka adalah 91. Jika sudah diketahui tiga siswa memperoleh nilai 100, satu siswa memperoleh nilai 96, tiga siswa memperoleh nilai 90. Serta dua siswa memperoleh nilai 86, maka nilai dua siswa yang belum diketahui yang paling mungkin adalah ...
A). 100 dan 100
B). 100 dan 90
C). 95 dan 90
D). 93 dan 91
E). 91 dan 86

$\spadesuit $ Jawaban : D
$\clubsuit $ Pembahasan :
$\spadesuit $ Konsep Dasar
*). Letak Median dan nilainya:
Jika $ n $ ganjil $ \rightarrow Me = X_{\frac{1}{2} (n+1)} $
Jika $ n $ genap $ \rightarrow Me = \frac{X_{\frac{n}{2}} + X_{\left( \frac{n}{2} + 1 \right)} }{2} $
Keterangan :
$ n = \, $ banyak data (total frekuensi)
$ X_k = \, $ data ke-$k$
Me = median

*). Misalkan 11 nilai yaitu :
$ X_1, X_2, X_3, X_4, X_5, ..., X_{10}, X_{11} $
dengan banyak data $ n = 11 $ (ganjil).
*). Median $ = 91 $ :
$\begin{align} Me & = 91 \\ X_{\frac{1}{2} (n+1)} & = 91 \\ X_{\frac{1}{2} (11+1)} & = 91 \\ X_6 & = 91 \end{align} $
*). Daftar nilai-nilai siswa yang sudah diketahui diurutkan dari kecil ke besar :
86, 86, 90, 90, 90, $ X_6 = 91 $ , 96, 100, 100, 100
*). Karena mediannya = 91, maka salah satu nilainya adalah 91. Nilai median adalah nilai siswa ke-6 dan nilai siswa ke-1 sampai ke-5 sudah ada, sehingga nilai satunya lagi harus nilai siswa ke-7 atau ke-8 atau ke-9 sampai ke-11 dengan nilainya berkisar 91 sampai 100.
*). Dapat kita simpulkan nilai dua siswa tersebut adalah 91 dan satunya lagi nilainya dari 91 sampai 100, namun dengan melihat option yang ada, maka nilai dua siswa yang mungkin adalah 91 dan 93.
Jadi, nilai dua siswa adalah 91 dan 93 $ . \, \heartsuit $

18). Soal UM UGM 2018 MatDas 286
Dua perusahaan masing-masing memiliki 6 karyawan dengan rata-rata usia karyawannya adalah 35 tahun dan 38 tahun. Jika satu orang di masing-masing perusahaan dipertukarkan, maka rata-rata kedua kelompok tersebut menjadi sama. Selisih usia kedua karyawan yang dipertukarkan tersebut adalah ...
A). $ 3 \, $
B). $ 6 \, $
C). $ 9 \, $
D). $ 12 \, $
E). $ 18 $

$\spadesuit $ Jawaban : C
$\clubsuit $ Pembahasan :
*). Misalkan perusahaannya adalah A dan B .
-). Perusahaan A :
$A_5 = \, $ jumlah total usia 5 orang yang tidak ditukar.
$ x_a = \, $ satu orang yang usianya ditukarkan.
rata - rata = 35
$ \frac{A_5 + x_a}{6} = 35 \rightarrow A_5 + x_a = 210 \, $ ....(i)
-). Perusahaan B :
$B_5 = \, $ jumlah total usia 5 orang yang tidak ditukar.
$ x_b = \, $ satu orang yang usianya ditukarkan.
rata - rata = 38
$ \frac{B_5 + x_b}{6} = 38 \rightarrow B_5 + x_b = 228 \, $ ....(ii)
*). Kurangkan pers(ii) dan (i) :
$\begin{array}{cc} B_5 + x_b = 228 & \\ A_5 + x_a = 210 & - \\ \hline \end{array} $
$ (B_5 - A_5) + (x_b - x_a) = 18 \, $ ....(iii)
*). Kedua orang ditukarkan ($x_a $ dan $ x_b $ ).
-). Perusahaan A menjadi : $ A_5 $ dan $ x_b $
-). Perusahaan B menjadi : $ B_5 $ dan $ x_a $
-). Rata-rata usia kedua perusahaan sama :
$ \frac{A_5 + x_b}{6} = \frac{B_5 + x_a}{6} \rightarrow A_5 + x_b = B_5 + x_a $
$ \rightarrow B_5 - A_5 = x_b - x_a \, $ ....(iv)
*). Substitusi pers(iv) ke pers(iii) :
$\begin{align} (B_5 - A_5) + (x_b - x_a) & = 18 \\ (x_b - x_a) + (x_b - x_a) & = 18 \\ 2(x_b - x_a) & = 18 \\ x_b - x_a & = 9 \end{align} $
Sehingga selisih usia kedua karyawan yang dipertukarkan tersebut adalah 9 .
Jadi, selisihnya adalah $ 9 . \, \heartsuit $

Perubahan Data

       Perubahan data secara beraturan yang dimaksud adalah setiap data dioperasikan ($+,-,\times , :$) dengan bilangan tertentu yang sama setiap datumnya. Untuk perubahan data secara beraturan, pengerjaannya biasanya lebih mudah.

Menyelesaikan perubahan data secara beraturan :
       Untuk perubahan data secara beraturan, pengukuran data kita bagi menjadi dua yaitu yang pertama ukuran pemusatan dan ukuran letak data, dan yang kedua ukuran penyebaran.
$\clubsuit $ Pengukuran pertama : ukuran pemusatan dan letak data yang terdiri dari Mean (rata-rata), modus, median, kuartil, desil, dan persentil.
Untuk pengukuran jenis pertama ini, nilanya berubah untuk semua jenis operasi($+,-,\times , :$).
$\clubsuit $ Pengukuran kedua : ukuran penyebaran yang terdiri dari jangkauan, simpangan, dan ragam.
Untuk pengukuran jenis kedua ini, nilainya berubah hanya untuk operasi perkalian ($\times$) dan pembagian ($:$).
Untuk Caranya : NGIKUT SOAL.

Berikut tabel ringkas perubahan data untuk semua jenis pengukuran :

       Untuk contoh mendetail, silahkan kunjungi link:
Perubahan data .

Contoh soal umptn:

19). Soal UM UGM 2017 MatDas 823
Sekumpulan bilangan mempunyai rata-rata 15 dengan jangkauan 6. Jika setiap bilangan tersebut dikurangi $ a $ kemudian hasilnya dibagi $ b $ akan menghasilkan bilangan baru dengan rata-rata 7 dan jangkauannya 3. Nilai $ a $ dan $ b $ berturut-turut adalah ....
A). 3 dan 2
B). 2 dan 3
C). 1 dan 2
D). 2 dan 1
E). 3 dan 1

$\spadesuit $ Jawaban : C
$\clubsuit $ Pembahasan :
$\spadesuit $ Konsep Dasar Statistika
*). Konsep perubahan data secara beraturan
-). Rata-rata berubah untuk semua operasi,
-). Jangkauan berubah untuk operasi kali dan bagi saja,
-). Cara pengerjaan : NGIKUT SOAL.
*). Misalkan terdapat rata-rata awal $\overline{X}_0 $ dan jangkauan awal $ J_0 $, kemudian data diubah dengan dikurangi $ a $ kemudian hasilnya dibagi $ b $ akan menghasilkan rata-rata baru $ \overline{X}_1 $ dan jangkauan baru $ J_1$, persamaannya :
$ J_1 = \frac{J_0}{b} $ dan $ \overline{X}_1 = \frac{\overline{X}_0 - a}{b} $

*). Diketahui data wala : $ \overline{X}_0 = 15 , \, J_0 = 6 $
Data diubah : kurangi $ a $ lalu dibagi $ b $ :
Data baru : $ \overline{X}_1 = 7 , \, J_b = 3 $
*). Menentukan nilai $ b $ :
$\begin{align} J_1 & = \frac{J_0}{b} \\ 3 & = \frac{6}{b} \\ b & = \frac{6}{3}= 2 \end{align} $
*). Menentukan niali $ a $ :
$\begin{align} \overline{X}_1 & = \frac{\overline{X}_0 - a}{b} \\ 7 & = \frac{15 - a}{2} \\ 14 & = 15 - a \\ a & = 1 \end{align} $
Jadi, nilai $ a = 1 $ dan $ b = 2 . \, \heartsuit $

       Tentu, beberapa contoh soal di atas masih terasa kurang jika benar-benar ingin menguasai berbagai variasi soal-soal Statistika seleksi PTN. Untuk lebih memaksimalkan belajarnya, silahkan sahabat koma kunjungi link berikut :
Kumpulan soal Statistika seleksi PTN .

       Demikian pembahasan materi Ringkasan Statistika - umptn dan contoh-contohnya. Silahkan juga baca materi lain yang berkaitan dengan UMPTN (Ujian Masuk Perguruan Tinggi Negeri) bidang Matematika pada link Daftar Materi UMPTN Bidang Matematika. Jika ada saran atau kritikan atau lainnya yang sifatnya membangaun, silahkan untuk tulis komen pada kolom komentar dibagian bawah setiap artikel. Semoga artikel ini bermanfaat. Terimakasih.