Blog KoMa - Pada artikel ini kita akan membahas materi Ringkasan Barisan dan Deret - umptn beserta
soal-soal yang terkait yang khususnya tentang soal-soal UMPTN baik seleksi bersama ataupun seleksi mandiri seperti SPMB, SNMPTN, SBMPTN, UTBK,
UM UGM (utul), simak UI, UM UNDIP, UNPAD, dan lainnya. Untuk melengkapkan materi dan memudahkan pemahaman, kami juga sertakan beberapa contoh soal
pendukung (bila diperlukan) untuk menguasai materi Barisan dan Deret ini. Untuk soal-soal Barisan dan Deret kita bagi menjadi dua
bagian yaitu contoh soal dan soal latihan mandiri. Untuk soal latihan mandiri, teman-teman bisa mencobanya terlebih dahulu, setelah itu baru cek solusinya
dibagian bawahnya untuk masing-masing soal latihan mandiri. Kami yakin, dengan tekun belajar maka materi Ringkasan Barisan dan Deret - umptn ini
bisa teman-teman kuasai dengan baik.
(A). Pengertian Barisan
Misalkan ada barisan : $ u_1, \, u_2, \, u_3, \, u_4, \, ... $
(i). Barisan Aritmetika: Selisih sama antara dua suku yang berdekatan, disebut dengan beda ($b$).
$ b = u_n - u_{n-1} = u_2 - u_1 = u_3 - u_2 = ... $
(ii). Barisan Geometri: Perbandingan dua suku yang berdekatan sama, disebut rasio ($r$).
$ r = \frac{u_n}{u_{n-1}} = \frac{u_2}{u_1} = \frac{u_3}{u_2} = \frac{...}{...} $
(i). Barisan Aritmetika: Selisih sama antara dua suku yang berdekatan, disebut dengan beda ($b$).
$ b = u_n - u_{n-1} = u_2 - u_1 = u_3 - u_2 = ... $
(ii). Barisan Geometri: Perbandingan dua suku yang berdekatan sama, disebut rasio ($r$).
$ r = \frac{u_n}{u_{n-1}} = \frac{u_2}{u_1} = \frac{u_3}{u_2} = \frac{...}{...} $
Untuk contoh detail dari pengertian barisan aritmetika dan barisan geometri, silahkan sahabat koma kunjungi link berikut ya:
Barisan dan deret Aritmetika
Barisan dan deret Geometri
Contoh soal umptn:
1). Soal SBMPTN 2013 MatDas 326
Diketahui $a, \, b,$ dan $c$ adalah tiga suku pertama suatu barisan aritmetika dengan $b > 0$ . Jika $a+b+c=b^2-4$ , maka nilai $b$ adalah ...
A). 2
B). 4
C). 5
D). 6
E). 7
Panjang sisi sebuah segitiga siku-siku membentuk barisan aritmetika. Jika keliling segitiga tersebut adalah 72, maka luasnya adalah ....
A). 216
B). 363
C). 364
D). 383
E). 432
Akar-akar persamaan kuadrat $ x^2 - (3p-2)x + ( 2p+8) = 0 \, $ adalah $ x_1 \, $ dan $ x_2 . \, $ Jika $ p \, $ positif dan $ x_1, p , x_2 \, $ membentuk barisan geometri, maka $ x_1 + p + x_2 = .... $
A). $ -11 \, $
B). $ -10 \, $
C). $ 12 \, $
D). $ 13 \, $
E). $ 14 $
(B). Rumus Suku ke-$n$ ($u_n$) dan suku tengah ($u_t$)
(i). Rumus suku ke-$n$ :
Aritmetika: $ u_n = a + (n-1)b $
Geometri: $ u_n = ar^{n-1} $
Keterangan:
$ a = \, $ suku pertama ($u_1$)
$ b = \, $ beda barisan aritmetika
$ r = \, $ rasio barisan geometri
$ u_n = \, $ suku ke-$n $
(ii). Rumus suku tengah:
Aritmetika: $ u_t = \frac{a + u_n}{2} $
Geometri: $ u_t = \sqrt{a \times u_n} $
Keterangan:
$ u_n = \, $ suku terakhirnya
$ u_t = \, $ suku tengahnya
Barisan memiliki suku tengah jika banyak sukunya ganjil.
Aritmetika: $ u_n = a + (n-1)b $
Geometri: $ u_n = ar^{n-1} $
Keterangan:
$ a = \, $ suku pertama ($u_1$)
$ b = \, $ beda barisan aritmetika
$ r = \, $ rasio barisan geometri
$ u_n = \, $ suku ke-$n $
(ii). Rumus suku tengah:
Aritmetika: $ u_t = \frac{a + u_n}{2} $
Geometri: $ u_t = \sqrt{a \times u_n} $
Keterangan:
$ u_n = \, $ suku terakhirnya
$ u_t = \, $ suku tengahnya
Barisan memiliki suku tengah jika banyak sukunya ganjil.
Contoh soal umptn:
4). Soal SBMPTN 2014 MatDas 654
Suku tengah suatu barisan aritmetika adalah 23. Jika suku terakhirnya 43 dan suku ketiganya 13, maka banyak suku barisan itu adalah ...
A). 5
B). 7
C). 9
D). 11
E). 13
Diketahui barisan aritmetika dengan $ U_n $ menyatakan suku ke-$n$. Jika $ U_{k+2} = U_2 + kU_{16} - 2 $ , maka nilai $ U_6 + U_{12} + U_{18} + U_{24} = .... $
A). $ \frac{2}{k} \, $
B). $ \frac{3}{k} \, $
C). $ \frac{4}{k} \, $
D). $ \frac{6}{k} \, $
E). $ \frac{8}{k} $
Berdasarkan penelitian diketahui bahwa populasi hewan A berkurang menjadi setengahnya tiap 10 tahun. Pada tahun 2000 populasinya tinggal 1 juta. Banyak populasi hewan A pada tahun 1960 sekitar ... juta.
A). 64
B). 32
C). 16
D). 8
E). 4
Diberikan barisan $U_n=\left\langle -1,1,-1,1,... \right\rangle $ dengan $n$ bilangan asli. Semua yang berikut merupakan rumus umum untuk barisan itu, kecuali ....
(A) $U_n=(-1)^n $
(B) $U_n=-\sin (n-\frac{1}{2})\pi $
(C) $U_n=-\cos (n-1)\pi $
(D) $U_n=-\sin (n-1)\pi $
(E) $U_n= \left\{ \begin{array}{c} -1, \, \text{jika} \, n \, \text{ganjil} \\ 1, \, \text{jika} \, n \, \text{genap} \end{array} \right. $
Diketahui perbandingan suku pertama dan suku ketiga dari suatu barisan aritmetika adalah 2 : 3. Perbandingan suku pertama dan suku kedua dari barisan tersebut adalah .....
A). 1 : 1
B). 2 : 5
C). 3 : 5
D). 4 : 5
E). 5 : 4
Suatu barisan geometri semua sukunya positif. Jika $ \frac{u_1+u_2}{u_3+u_4}=\frac{1}{9} \, $ maka $ \frac{u_1 + u_2+u_3+u_4}{u_2+u_3}= .... $
A). $ \frac{10}{9} \, $
B). $ 3 \, $
C). $ \frac{10}{3} \, $
D). $ 4 \, $
E). $ 10 $
Empat bilangan membentuk suatu barisan aritmetika. Jika bilangan pertama dan bilangan kedua tetap, serta bilangan ketiga ditambah bilangan pertama dan bilangan keempat dikali 2, maka terbentuk suatu barisan geometri. Jika beda suku-suku pada barisan aritmatika adalah 2, maka jumlah empat bilangan pertama pada barisan geometri tersebut adalah ...
A). $ 8 \, $
B). $ 20 \, $
C). $ 24 \, $
D). $ 30 \, $
E). $ 36 $
(C). Sisipan
Awalnya terdapat barisan : $ u_1, u_2, u_3, ... $
Kemudian disisipkan $ k $ suku atau $ k $ bilangan diantara dua suku yang berdekatan, sehingga diperoleh barisan baru.
$ \underbrace{u_1 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, u_2}_{\text{sisipkan } k \text{ suku}} \, \underbrace{ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, u_3}_{\text{sisipkan } k \text{ suku}} \, \underbrace{ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, u_4}_{\text{sisipkan } k \text{ suku}} \, \, \, \, ... \, ... $
Diperoleh beda baru ($b^*$) dan rasio baru ($r^*$):
$ b^* = \frac{b}{k+1} $
$ r^* = \sqrt[k+1]{r} \, $ atau $ r^* = r^\frac{1}{k+1} $
Keterangan:
$ b^* = \, $ beda baru
$ r^* = \, $ rasio baru
$ b = \, $ beda awal
$ r = \, $ rasio awal
Kemudian disisipkan $ k $ suku atau $ k $ bilangan diantara dua suku yang berdekatan, sehingga diperoleh barisan baru.
$ \underbrace{u_1 \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, u_2}_{\text{sisipkan } k \text{ suku}} \, \underbrace{ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, u_3}_{\text{sisipkan } k \text{ suku}} \, \underbrace{ \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, \, u_4}_{\text{sisipkan } k \text{ suku}} \, \, \, \, ... \, ... $
Diperoleh beda baru ($b^*$) dan rasio baru ($r^*$):
$ b^* = \frac{b}{k+1} $
$ r^* = \sqrt[k+1]{r} \, $ atau $ r^* = r^\frac{1}{k+1} $
Keterangan:
$ b^* = \, $ beda baru
$ r^* = \, $ rasio baru
$ b = \, $ beda awal
$ r = \, $ rasio awal
Contoh soal umptn:
11). Soal UMB 2008 MatDas 441
Jika di antara 7 dan 448 disisipkan lima bilangan positif sehingga membentuk suatu barisan geometri, maka jumlah suku kedua dan suku keenamnya sama dengan ... ?
A). 126
B). 231
C). 238
D). 455
E). 462
(D). Rumus Jumlah $ n $ Suku Pertama ($s_n$)
(i). Deret Aritmetika:
(1). $ s_n = \frac{n}{2} (a + u_n) $
(2). $ s_n = \frac{n}{2} (2a + (n-1)b) $
(3). $ s_n = n. u_t $
(ii). Deret Geometri:
$ s_n = \frac{a(r^n - 1)}{r-1} \, $ untuk $ r > 1 $
$ s_n = \frac{a(1 - r^n )}{1 - r} \, $ untuk $ r < 1 $
(iii). Hubungan $ u_n $ dan $ s_n $ :
untuk $ n = 1 \rightarrow u_1 = s_1 $
untuk $ n > 1 \rightarrow u_n = s_n - s_{(n-1)} $
(iv). Khusus deret Aritmetika:
Bentuk umum $ s_n $ nya yaitu : $ s_n = pn^2 + qn $
dengan beda: $ b = 2p $
(1). $ s_n = \frac{n}{2} (a + u_n) $
(2). $ s_n = \frac{n}{2} (2a + (n-1)b) $
(3). $ s_n = n. u_t $
(ii). Deret Geometri:
$ s_n = \frac{a(r^n - 1)}{r-1} \, $ untuk $ r > 1 $
$ s_n = \frac{a(1 - r^n )}{1 - r} \, $ untuk $ r < 1 $
(iii). Hubungan $ u_n $ dan $ s_n $ :
untuk $ n = 1 \rightarrow u_1 = s_1 $
untuk $ n > 1 \rightarrow u_n = s_n - s_{(n-1)} $
(iv). Khusus deret Aritmetika:
Bentuk umum $ s_n $ nya yaitu : $ s_n = pn^2 + qn $
dengan beda: $ b = 2p $
Contoh soal umptn:
12). Soal SBMPTN 2014 MatDas 613
Jumlah suku ke-4 dan suku ke-5 dari suatu barisan aritmetika adalah 55, sedangkan suku ke-9 dikurangi dua kali suku ke-2 bernilai 1. Jumlah tiga suku pertama barisan tersebut adalah ...
A). 17
B). 35
C). 37
D). 40
E). 60
Suku pertama barisan aritmetika adalah $ a $ dan bedanya $ 2a $. Jika nilai $ U_1 + U_2 + U_3+U_4+U_5 = 100 $ , maka nilai $ U_2 + U_3 + U_4 + ... + U_{20} = .... $
A). $ 1590 \, $
B). $ 1596 \, $
C). $ 1600 \, $
D). $ 1690 \, $
E). $ 1700 $
Dalam suatu barisan aritmatika, nilai rata-rata dari 4 suku pertama adalah 8 dan nilai rata-rata 9 suku pertama adalah 3. Jumlah $n$ suku pertama barisan tersebut adalah ...
A). $ -10n + n^2 $
B). $ 11n + n^2 $
C). $ 12n - n^2 $
D). $ -10n - n^2 $
E). $ 8n - n^2 $
Jika $S_n=5n^2-6n$ adalah jumlah $n$ suku pertama barisan aritmetika, maka suku ke-5 barisan tersebut adalah ...
A). 51
B). 41
C). 39
D). 29
E). 20
Jika jumlah $n $ suku pertama deret aritmetika adalah $ S_n = 2n^2+3n $ , maka beda deretnya adalah ....
A). 2
B). 3
C). 4
D). 5
E). 6
Jika $ a+2, \, a - 2, \, 2 $ membentuk barisan geometri, maka jumlah 11 suku pertama yang mungkin adalah ...?
A). 0
B). 1
C). 2
D). 3
E). 4
(E). Deret Geometri Tak Hingga
Misalkan ada deret $ u_1 + u_2 + u_3 + u_4 + .... \, $ yang dijumlahkan sampai tak hingga yang disimbolkan dengan $ s_\infty $.
Hasil jumlah tak hingganya ($s_\infty$) tergantng dari nilai rasionya ($r$).
a). Jika $ r > 1 , \, $ maka hasil penjumlahannya : $ s_\infty = + \infty $
b). Jika $ -1 < r < 1 , \, $ maka hasil penjumlahannya : $ s_\infty = \frac{a}{1-r} $
c). Jika $ r < -1 , \, $ maka hasil penjumlahannya : $ s_\infty = - \infty $
Secara umum nilai jumlah tak hingga deret geometri dengan rasio $ -1 < r < 1 \, $ adalah $ s_\infty = \frac{\text{suku pertama}}{1 - \text{ rasio}} $
Pada penjumlahan deret geometri tak hingga, ada dua istilah yaitu :
1). Konvergen (deret konvergen) syaratnya $ -1 < r < 1 , \, $ artinya jumlah sampai tak hingganya memberikan hasil angka tertentu (hasilnya bukan $ +\infty \, $ atau $ - \infty $)
2). Divergen (deret divergen) syaratnya $ r < -1 \, $ atau $ r > 1 , \, $ artinya jumlah sampai tak hingganya memberikan hasil $ +\infty \, $ atau $ - \infty $
a). Jika $ r > 1 , \, $ maka hasil penjumlahannya : $ s_\infty = + \infty $
b). Jika $ -1 < r < 1 , \, $ maka hasil penjumlahannya : $ s_\infty = \frac{a}{1-r} $
c). Jika $ r < -1 , \, $ maka hasil penjumlahannya : $ s_\infty = - \infty $
Secara umum nilai jumlah tak hingga deret geometri dengan rasio $ -1 < r < 1 \, $ adalah $ s_\infty = \frac{\text{suku pertama}}{1 - \text{ rasio}} $
Pada penjumlahan deret geometri tak hingga, ada dua istilah yaitu :
1). Konvergen (deret konvergen) syaratnya $ -1 < r < 1 , \, $ artinya jumlah sampai tak hingganya memberikan hasil angka tertentu (hasilnya bukan $ +\infty \, $ atau $ - \infty $)
2). Divergen (deret divergen) syaratnya $ r < -1 \, $ atau $ r > 1 , \, $ artinya jumlah sampai tak hingganya memberikan hasil $ +\infty \, $ atau $ - \infty $
Untuk contoh mendetail tentang deret geometri tak hingga, silahkan teman-teman kunjungi link:
Deret Geometri Tak Hingga
Contoh soal umptn:
18). Soal SPMK UB 2013 MatIPA
Jika $x+\frac{1}{x} + \frac{1}{x^3} + \frac{1}{x^5} + ... = 2x $ , maka nilai $x$ yang mungkin adalah ....
(1). $-\sqrt{2} $ (2). -2 (3). $\sqrt{2}$ (4). 2
(Gunakan Petunjuk C untuk menjawab soal ini)
(F). Deret Tak Hingga Genap dan Ganjil
Misalkan ada deret geomeri tak hingga $ u_1 + u_2 + u_3 + u_4 + u_5 .... \, $
Deret tersebut bisa dibagi menjadi dua bagian yaitu suku-suku bernomor genap dan ganjil
$ \begin{align} s_\infty & = u_1 + u_2 + u_3 + u_4 + u_5 + u_6 .... \\ s_\infty & = (u_1 + u_3 + u_5+... ) + (u_2 + u_4 + u_6 ....) \\ s_\infty & = s_{\infty \text{ ganjil}} + s_{\infty \text{ genap}} \end{align} $
Artinya jumlah takhingga merupakan penjumlahan jumlah takhingga nomor ganjil dengan jumlah takhingga nomor genap.
Rumus takhingga nomor ganjil dan nomor genap.
$ \begin{align} s_{\infty \text{ ganjil}} & = u_1 + u_3 + u_5+... \\ & = a + ar^2 + ar^3 +... \\ & \left( \text{rasio} = \frac{ar^2}{a} = r^2 \right) \\ & \left( \text{suku pertama} = a \right) \\ & = \frac{\text{suku pertama}}{1 - \text{ rasio}} \\ s_{\infty \text{ ganjil}} & = \frac{a}{1 - r^2} \end{align} $
Sehingga rumus jumlah takhingga nomor ganjil : $ s_{\infty \text{ ganjil}} = \frac{a}{1 - r^2} $
$ \begin{align} s_{\infty \text{ genap}} & = u_2 + u_4 + u_6+... \\ & = ar + ar^3 + ar^5 +... \\ & \text{rasio} = \frac{ar^3}{ar} = r^2 \\ & \text{suku pertama} = ar \\ & = \frac{\text{suku pertama}}{1 - \text{ rasio}} \\ s_{\infty \text{ genap}} & = \frac{ar}{1 - r^2} \end{align} $
Sehingga rumus jumlah takhingga nomor genap : $ s_{\infty \text{ genap}} = \frac{ar}{1 - r^2} $
Menentukan rasio dari jumlah takhingga nomor ganjil dan genap.
$ \begin{align} \frac{s_{\infty \text{ genap}}}{s_{\infty \text{ ganjil}}} & = \frac{\frac{ar}{1 - r^2}}{\frac{a}{1 - r^2}} \\ & = \frac{\frac{ar}{1 - r^2}}{\frac{a}{1 - r^2}} \\ & = \frac{ar}{1 - r^2} . \frac{1-r^2}{a} \\ & = \frac{ar(1-r^2)}{a(1 - r^2)} \\ \frac{s_{\infty \text{ genap}}}{s_{\infty \text{ ganjil}}} & = r \end{align} $
Artinya untuk menentukan rasionya, cukup gunakan $ r = \frac{s_{\infty \text{ genap}}}{s_{\infty \text{ ganjil}}} $
Deret tersebut bisa dibagi menjadi dua bagian yaitu suku-suku bernomor genap dan ganjil
$ \begin{align} s_\infty & = u_1 + u_2 + u_3 + u_4 + u_5 + u_6 .... \\ s_\infty & = (u_1 + u_3 + u_5+... ) + (u_2 + u_4 + u_6 ....) \\ s_\infty & = s_{\infty \text{ ganjil}} + s_{\infty \text{ genap}} \end{align} $
Artinya jumlah takhingga merupakan penjumlahan jumlah takhingga nomor ganjil dengan jumlah takhingga nomor genap.
Rumus takhingga nomor ganjil dan nomor genap.
$ \begin{align} s_{\infty \text{ ganjil}} & = u_1 + u_3 + u_5+... \\ & = a + ar^2 + ar^3 +... \\ & \left( \text{rasio} = \frac{ar^2}{a} = r^2 \right) \\ & \left( \text{suku pertama} = a \right) \\ & = \frac{\text{suku pertama}}{1 - \text{ rasio}} \\ s_{\infty \text{ ganjil}} & = \frac{a}{1 - r^2} \end{align} $
Sehingga rumus jumlah takhingga nomor ganjil : $ s_{\infty \text{ ganjil}} = \frac{a}{1 - r^2} $
$ \begin{align} s_{\infty \text{ genap}} & = u_2 + u_4 + u_6+... \\ & = ar + ar^3 + ar^5 +... \\ & \text{rasio} = \frac{ar^3}{ar} = r^2 \\ & \text{suku pertama} = ar \\ & = \frac{\text{suku pertama}}{1 - \text{ rasio}} \\ s_{\infty \text{ genap}} & = \frac{ar}{1 - r^2} \end{align} $
Sehingga rumus jumlah takhingga nomor genap : $ s_{\infty \text{ genap}} = \frac{ar}{1 - r^2} $
Menentukan rasio dari jumlah takhingga nomor ganjil dan genap.
$ \begin{align} \frac{s_{\infty \text{ genap}}}{s_{\infty \text{ ganjil}}} & = \frac{\frac{ar}{1 - r^2}}{\frac{a}{1 - r^2}} \\ & = \frac{\frac{ar}{1 - r^2}}{\frac{a}{1 - r^2}} \\ & = \frac{ar}{1 - r^2} . \frac{1-r^2}{a} \\ & = \frac{ar(1-r^2)}{a(1 - r^2)} \\ \frac{s_{\infty \text{ genap}}}{s_{\infty \text{ ganjil}}} & = r \end{align} $
Artinya untuk menentukan rasionya, cukup gunakan $ r = \frac{s_{\infty \text{ genap}}}{s_{\infty \text{ ganjil}}} $
Contoh soal umptn:
19). Soal SBMPTN 2013 MatIPA 326
Diketahui deret geometri tak hingga $u_1+u_2+u_3+...$ . Jika rasio deret tersebut adalah $r$ dengan $ -1 < r < 1 $ , $u_2+u_4+u_6...=4$ , dan $u_2+u_4=3$ , maka nilai $r^2$ adalah ...
A). $ \frac{1}{4} $
B). $ \frac{1}{3} $
C). $ \frac{\sqrt{3}}{2} $
D). $ \frac{1}{2} $
E). $ \frac{3}{4} $
Jumlah semua suku bernomor ganjil dari deret geometri tak hingga adalah 4. Jika jumlah deret itu adalah 6, maka jumlah dua suku pertamanya adalah ...
A). $ \frac{15}{4} $
B). $ \frac{27}{8} $
C). $ \frac{9}{2} $
D). $ \frac{9}{8} $
E). $ \frac{7}{8} $
(G). Kejadian Bola dan Ayunan
Kejadian pelemparan benda yang dimaksud biasanya bola yang dijatuhkan atau bola dilempar ke atas. Berikut penjelasan
dua kasus yang dimaksud :
Bola dilempar ke atas
Misalkan bola dilempar ke atas, terbentuklah lintasan yang dilalui oleh bola tersebut seperti gambar berikut :
keterangan :
$ a = \, $ ketianggian awal yang dicapai oleh bola
$ r = \, $ rasio ketinggian setelah terjadi pantulan dari ketinggian sebelumnya.
Dari lintasan yang dilalui oleh bola, ada bagian yang naik dan ada bagian yang turun. Masing-masing bagian naik total panjang lintasannya adalah $ s_\infty \, $ dan bagian yang turun juga panjang lintasannya $ s_\infty $. Sehingga total panjang lintasan (PL) yang dilalui oleh bola adalah :
$ \begin{align} \text{total panjang lintasan} & = \text{Lintasan naik } + \text{ lintasan turun} \\ PL & = s_\infty + s_\infty \\ PL & = 2s\infty \\ PL & = 2\left( \frac{a}{1-r} \right) \\ PL & = \frac{2a}{1-r} \end{align} $
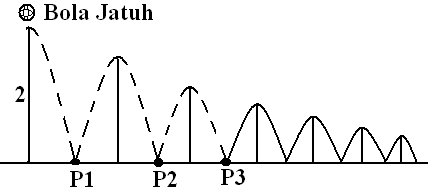
Bola dijatuhkan dari ketinggian awal $ a $
Lintasan yang terbentuk ketika bola dijatuhkan hampir sama dengan lintasan yang terbentuk ketika bola dilempar ke atas. Hanya saja satu lintasan awal (lintasan naik awal) tidak dihitung karena bola langsung dijatukan. Berikut gambar lintasannya :
Dari gambar bola dijatuhkan, terlihat bahwa lintasannya sama dengan bola dilempar ke atas, hanya saja satu lintasan naik ($a$) tidak dihitung. Sehingga total panjang lintasannya adalah :
$ PL = 2s_\infty - a $
$ PL = 2\left( \frac{a}{1-r} \right) - a $
Panjang Lintasan setelah pantulan ke-$k$
Untuk kasus panjang lintasan setelah pantulan ke-$k \, $ baik bola dijatuhkan atau dilempar ke atas hasilnya akan selalu sama.
Dari gambar terlihat bahwa setelah pantulan ke-1 maka suku pertamanya adalah suku ke-2 ($u_2$), setelah pantulan ke-2 maka suku pertamanya adalah suku ke-3 ($u_3$), setelah pantulan ke-3 maka suku pertamanya adalah suku ke-4 ($u_4$), dan seterusnya sampai setelah pantulan ke-$k\,$ maka suku pertamanya adalah suku ke-$k+1\,$ ($u_{k+1}$)
Dapat disusun rumus panjang lintasannya dengan $ u_n = ar^{n-1} $ :
Panjang lintasan setelah pantulan ke-1 :
$ PL = 2s_\infty = 2. \frac{\text{suku pertama}}{1 - \text{ rasio}} = 2. \frac{u_2}{1 - r} = 2. \frac{ar}{1 - r} $
Panjang lintasan setelah pantulan ke-2 :
$ PL = 2s_\infty = 2. \frac{\text{suku pertama}}{1 - \text{ rasio}} = 2. \frac{u_3}{1 - r} = 2. \frac{ar^2}{1 - r} $
Panjang lintasan setelah pantulan ke-3 :
$ PL = 2s_\infty = 2. \frac{\text{suku pertama}}{1 - \text{ rasio}} = 2. \frac{u_4}{1 - r} = 2. \frac{ar^3}{1 - r} $
dan seterusnya .....
Panjang lintasan setelah pantulan ke-$k$ :
$ PL = 2s_\infty = 2. \frac{\text{suku pertama}}{1 - \text{ rasio}} = 2. \frac{u_{k+1}}{1 - r} = 2. \frac{ar^k}{1 - r} $
Jadi dapat diperumum, panjang lintasan bila bola dijatuhkan atau dilempar ke atas setelah pantulan ke-$k \, $ adalah
$ PL = 2 \times \frac{ar^k}{1 - r} $
Untuk kejadian pada ayunan, panjang lintasannya:
PL $ = s_\infty = \frac{a}{1-r} $
Bola dilempar ke atas
Misalkan bola dilempar ke atas, terbentuklah lintasan yang dilalui oleh bola tersebut seperti gambar berikut :
keterangan :
$ a = \, $ ketianggian awal yang dicapai oleh bola
$ r = \, $ rasio ketinggian setelah terjadi pantulan dari ketinggian sebelumnya.
Dari lintasan yang dilalui oleh bola, ada bagian yang naik dan ada bagian yang turun. Masing-masing bagian naik total panjang lintasannya adalah $ s_\infty \, $ dan bagian yang turun juga panjang lintasannya $ s_\infty $. Sehingga total panjang lintasan (PL) yang dilalui oleh bola adalah :
$ \begin{align} \text{total panjang lintasan} & = \text{Lintasan naik } + \text{ lintasan turun} \\ PL & = s_\infty + s_\infty \\ PL & = 2s\infty \\ PL & = 2\left( \frac{a}{1-r} \right) \\ PL & = \frac{2a}{1-r} \end{align} $
Bola dijatuhkan dari ketinggian awal $ a $
Lintasan yang terbentuk ketika bola dijatuhkan hampir sama dengan lintasan yang terbentuk ketika bola dilempar ke atas. Hanya saja satu lintasan awal (lintasan naik awal) tidak dihitung karena bola langsung dijatukan. Berikut gambar lintasannya :
Dari gambar bola dijatuhkan, terlihat bahwa lintasannya sama dengan bola dilempar ke atas, hanya saja satu lintasan naik ($a$) tidak dihitung. Sehingga total panjang lintasannya adalah :
$ PL = 2s_\infty - a $
$ PL = 2\left( \frac{a}{1-r} \right) - a $
Panjang Lintasan setelah pantulan ke-$k$
Untuk kasus panjang lintasan setelah pantulan ke-$k \, $ baik bola dijatuhkan atau dilempar ke atas hasilnya akan selalu sama.
Dari gambar terlihat bahwa setelah pantulan ke-1 maka suku pertamanya adalah suku ke-2 ($u_2$), setelah pantulan ke-2 maka suku pertamanya adalah suku ke-3 ($u_3$), setelah pantulan ke-3 maka suku pertamanya adalah suku ke-4 ($u_4$), dan seterusnya sampai setelah pantulan ke-$k\,$ maka suku pertamanya adalah suku ke-$k+1\,$ ($u_{k+1}$)
Dapat disusun rumus panjang lintasannya dengan $ u_n = ar^{n-1} $ :
Panjang lintasan setelah pantulan ke-1 :
$ PL = 2s_\infty = 2. \frac{\text{suku pertama}}{1 - \text{ rasio}} = 2. \frac{u_2}{1 - r} = 2. \frac{ar}{1 - r} $
Panjang lintasan setelah pantulan ke-2 :
$ PL = 2s_\infty = 2. \frac{\text{suku pertama}}{1 - \text{ rasio}} = 2. \frac{u_3}{1 - r} = 2. \frac{ar^2}{1 - r} $
Panjang lintasan setelah pantulan ke-3 :
$ PL = 2s_\infty = 2. \frac{\text{suku pertama}}{1 - \text{ rasio}} = 2. \frac{u_4}{1 - r} = 2. \frac{ar^3}{1 - r} $
dan seterusnya .....
Panjang lintasan setelah pantulan ke-$k$ :
$ PL = 2s_\infty = 2. \frac{\text{suku pertama}}{1 - \text{ rasio}} = 2. \frac{u_{k+1}}{1 - r} = 2. \frac{ar^k}{1 - r} $
Jadi dapat diperumum, panjang lintasan bila bola dijatuhkan atau dilempar ke atas setelah pantulan ke-$k \, $ adalah
$ PL = 2 \times \frac{ar^k}{1 - r} $
Untuk kejadian pada ayunan, panjang lintasannya:
PL $ = s_\infty = \frac{a}{1-r} $
Contoh soal umptn:
21). Soal UMPTN 2000 MatDas
Sebuah bola pingpong dijatuhkan kelantai dari ketinggian 2 meter. Setiap kali setiap bola itu memantul ia mencapai ketinggian tiga per empat dari ketinggian yang dicapai sebelumnya. Panjang lintasan bola tersebut dari pantulan ke-3 sampai berhenti adalah ...
A). 3,38 meter
B). 3,75 meter
C). 4,25 meter
D). 6,75 meter
E). 7,75 meter
(H). Penerapan pada Bunga Bank
(i). Rumus Bunga Tunggal :
$ M_n = M_o (1 + n \times i ) $
(ii). Rumus Bunga Majemuk :
$ M_n = M_o (1 + i )^n $
Keterangan:
$ M_n = \, $ tabungan/pinjaman/modal akhir
$ M_o = \, $ tabungan/pinjaman/modal awal
$ n = \, $ periode lama menabung
$ i = \, $ suku bunga dalam persen.
$ M_n = M_o (1 + n \times i ) $
(ii). Rumus Bunga Majemuk :
$ M_n = M_o (1 + i )^n $
Keterangan:
$ M_n = \, $ tabungan/pinjaman/modal akhir
$ M_o = \, $ tabungan/pinjaman/modal awal
$ n = \, $ periode lama menabung
$ i = \, $ suku bunga dalam persen.
Contoh soal umptn:
22). Soal UTBK 2019 Saintek
Budi menabung di bank dengan saldo awal A dengan sistem bunga majemuk, 3 tahun kemudian saldonya menjadi B. Wati menabung di bank yang sama dengan saldo awal $ x $, saldo Wati 6 tahun kemudian menjadi 3 kali dari saldo akhir Budi. Besarnya saldo awal Wati adalah ....
A). $ \frac{2A^2}{B} \, $
B). $ \frac{3A^2}{B} \, $
C). $ 4AB^2 \, $
D). $ \frac{A^2}{4B} \, $
E). $ \frac{A^2}{2B} $
Tentu, beberapa contoh soal di atas masih terasa kurang jika benar-benar ingin menguasai berbagai variasi soal-soal Barisan dan Deret seleksi PTN. Untuk lebih memaksimalkan belajarnya, silahkan sahabat koma kunjungi link berikut :
Kumpulan soal Barisan dan Deret seleksi PTN .
Demikian pembahasan materi Ringkasan Barisan dan Deret - umptn dan contoh-contohnya. Silahkan juga baca materi lain yang berkaitan dengan UMPTN (Ujian Masuk Perguruan Tinggi Negeri) bidang Matematika pada link Daftar Materi UMPTN Bidang Matematika. Jika ada saran atau kritikan atau lainnya yang sifatnya membangaun, silahkan untuk tulis komen pada kolom komentar dibagian bawah setiap artikel. Semoga artikel ini bermanfaat. Terimakasih.