Untuk Latihan 4.2 Garis dan sudut kelas VII Kurikulum 2013 ini tentu soal-soalnya lebih kompleks dan lebih rumit lagi dibandingkan dengan soal-soal pada latihan 4.1 sebelumnya. Konsep yang digunakanpun sudah lebih berkembang untuk menjawab latihan 4.2. Saran kami, sebaiknya teman-teman menguasai dulu materi yang terkait dengan soal-soalnya, setelah itu pasti akan dengan mudah bisa menjawab atau mudah memahami pembahasan yang ada pada artikel ini.
Soal 1.
Nyatakan setiap sudut di bawah ini, apakah termasuk sudut lancip, tumpul,
atau siku-siku. Serta gambarkan setiap sudut tersebut.
a). $ \frac{1}{3} \, $ sudut lurus
b). $ \frac{2}{3} \, $ putaran penuh
c). $ 180^\circ - \frac{5}{6} \, $ Sudut lurus
a). $ \frac{1}{3} \, $ sudut lurus
b). $ \frac{2}{3} \, $ putaran penuh
c). $ 180^\circ - \frac{5}{6} \, $ Sudut lurus
Penyelesaian :
a). $ \frac{1}{3} \, $ sudut lurus $ = \frac{1}{3} . 180^\circ = 60^\circ $
Sudut ini termasuk sudut lancip karena antara $ 0^\circ \, $ dan $ \, 90^\circ $ .
b). $ \frac{2}{3} \, $ putaran penuh $ = \frac{2}{3} . 360^\circ = 240^\circ $
Sudut ini termasuk sudut refleks karena antara $ 180^\circ \, $ dan $ \, 360^\circ $ .
c). $ 180^\circ - \frac{5}{6} \, $ Sudut lurus = $ 180^\circ - \frac{5}{6} . 180^\circ = 180^\circ - 150^\circ = 30^\circ $
Sudut ini termasuk sudut lancip karena antara $ 0^\circ \, $ dan $ \, 90^\circ $ .
Catatan : Untuk gambarnya, silahkan teman-teman coba sendiri ya.
a). $ \frac{1}{3} \, $ sudut lurus $ = \frac{1}{3} . 180^\circ = 60^\circ $
Sudut ini termasuk sudut lancip karena antara $ 0^\circ \, $ dan $ \, 90^\circ $ .
b). $ \frac{2}{3} \, $ putaran penuh $ = \frac{2}{3} . 360^\circ = 240^\circ $
Sudut ini termasuk sudut refleks karena antara $ 180^\circ \, $ dan $ \, 360^\circ $ .
c). $ 180^\circ - \frac{5}{6} \, $ Sudut lurus = $ 180^\circ - \frac{5}{6} . 180^\circ = 180^\circ - 150^\circ = 30^\circ $
Sudut ini termasuk sudut lancip karena antara $ 0^\circ \, $ dan $ \, 90^\circ $ .
Catatan : Untuk gambarnya, silahkan teman-teman coba sendiri ya.
Soal 2.
Manakah dari pernyataan berikut ini yang benar? Jelaskan.
a. Jika $\angle $A dan $\angle $B berpelurus, maka m$\angle $A tidak mungkin sama dengan m$\angle $B.
b. Jika $\angle $A adalah sudut tumpul, maka pelurus $\angle $A pasti sudut lancip.
c. Jika sudut penyiku $\angle $A kurang dari 30$^\circ $ , maka pelurus $\angle $A adalah sudut tumpul.
a. Jika $\angle $A dan $\angle $B berpelurus, maka m$\angle $A tidak mungkin sama dengan m$\angle $B.
b. Jika $\angle $A adalah sudut tumpul, maka pelurus $\angle $A pasti sudut lancip.
c. Jika sudut penyiku $\angle $A kurang dari 30$^\circ $ , maka pelurus $\angle $A adalah sudut tumpul.
Penyelesaian :
a). $\angle $A dan $\angle $B berpelurus , maka $ \angle A + \angle B = 180^\circ $ ,
artinya kemungkinan bisa besar kedua sudut sama besar yaitu $ \angle A = 90^\circ \, $ dan $ \angle B = 90^\circ \, $
Sehingga pernyataan a ini masih salah.
b). Karena $ \angle $ A tumpul maka sudutnya lebih besar dari $ 90^\circ $ ( $ \angle A > 90^\circ $) .
Pelurus dari $ \angle A = 180^\circ - \angle A \, $ .
Karena besar $ \angle A > 90^\circ $ , maka pastilah $ 180^\circ - \angle A < 90^\circ \, $ yang artinya sudut pelurusnya adalah sudut lancip.
Sehingga pernyataan b benar.
c). Misalkan sudut penyiku dari $ \angle $ A adalah $ \angle $B,
Jika sudut penyiku $\angle $A kurang dari 30$^\circ $ , artinya $ \angle B < 30^\circ \, $
Sehingga : $ \angle A + \angle B = 90^\circ \rightarrow \angle A = 90^\circ - \angle B $
Karena $ \angle B < 30^\circ \, $ maka besar $ \angle A \, $ adalah $ 30^\circ \leq \angle A \leq 90^\circ $ .
*). Misalkan pelurus $ \angle A \, $ adalah $ \angle C $.
$ \angle C = 180^\circ - \angle A \, $
Karena besar sudut A adalah $ 30^\circ \leq \angle A \leq 90^\circ $
sehingga Pelurus sudut A adalah $ 90^\circ < \angle C < 150^\circ $
Artinya pelurus sudut A adalah sudut tumpul,
Sehingga pernyataan c benar.
a). $\angle $A dan $\angle $B berpelurus , maka $ \angle A + \angle B = 180^\circ $ ,
artinya kemungkinan bisa besar kedua sudut sama besar yaitu $ \angle A = 90^\circ \, $ dan $ \angle B = 90^\circ \, $
Sehingga pernyataan a ini masih salah.
b). Karena $ \angle $ A tumpul maka sudutnya lebih besar dari $ 90^\circ $ ( $ \angle A > 90^\circ $) .
Pelurus dari $ \angle A = 180^\circ - \angle A \, $ .
Karena besar $ \angle A > 90^\circ $ , maka pastilah $ 180^\circ - \angle A < 90^\circ \, $ yang artinya sudut pelurusnya adalah sudut lancip.
Sehingga pernyataan b benar.
c). Misalkan sudut penyiku dari $ \angle $ A adalah $ \angle $B,
Jika sudut penyiku $\angle $A kurang dari 30$^\circ $ , artinya $ \angle B < 30^\circ \, $
Sehingga : $ \angle A + \angle B = 90^\circ \rightarrow \angle A = 90^\circ - \angle B $
Karena $ \angle B < 30^\circ \, $ maka besar $ \angle A \, $ adalah $ 30^\circ \leq \angle A \leq 90^\circ $ .
*). Misalkan pelurus $ \angle A \, $ adalah $ \angle C $.
$ \angle C = 180^\circ - \angle A \, $
Karena besar sudut A adalah $ 30^\circ \leq \angle A \leq 90^\circ $
sehingga Pelurus sudut A adalah $ 90^\circ < \angle C < 150^\circ $
Artinya pelurus sudut A adalah sudut tumpul,
Sehingga pernyataan c benar.
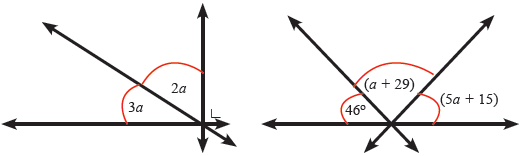
Soal 3.
Penyelesaian :
*). Gambar 1,
Sudut $ 3a \, $ dan $ 2a \, $ membentuk sudut siku-siku (berpenyiku), sehingga jumlahnya $ 90^\circ $ .
$ 3a + 2a = 90^\circ \rightarrow 5a = 90^\circ \rightarrow a = \frac{90^\circ}{5} = 18^\circ $
Jadi, dari gambar 1, nilai $ a = 18^\circ $ .
*). Gambar 2,
Sudut $ 46^\circ, \, (a+29), \, $ dan $ (5a+15) \, $ membentuk sudut lurus (berpelurus), sehingga jumlahnya $ 180^\circ $ .
$ 46^\circ + (a+29) + (5a+15) = 180^\circ \rightarrow 90^\circ + 6a = 180^\circ $
$ 6a = 180^\circ - 90^\circ = 90^\circ \rightarrow a = \frac{90^\circ}{6} = 15^\circ $
Jadi, dari gambar 2, nilai $ a = 15^\circ $ .
*). Gambar 1,
Sudut $ 3a \, $ dan $ 2a \, $ membentuk sudut siku-siku (berpenyiku), sehingga jumlahnya $ 90^\circ $ .
$ 3a + 2a = 90^\circ \rightarrow 5a = 90^\circ \rightarrow a = \frac{90^\circ}{5} = 18^\circ $
Jadi, dari gambar 1, nilai $ a = 18^\circ $ .
*). Gambar 2,
Sudut $ 46^\circ, \, (a+29), \, $ dan $ (5a+15) \, $ membentuk sudut lurus (berpelurus), sehingga jumlahnya $ 180^\circ $ .
$ 46^\circ + (a+29) + (5a+15) = 180^\circ \rightarrow 90^\circ + 6a = 180^\circ $
$ 6a = 180^\circ - 90^\circ = 90^\circ \rightarrow a = \frac{90^\circ}{6} = 15^\circ $
Jadi, dari gambar 2, nilai $ a = 15^\circ $ .
Soal 4.
Diketahui m$\angle $A = $ \frac{2}{3} $ m$\angle $B. Tentukan
a. m$\angle $A dan m$\angle $B jika keduanya saling berpelurus. b. Selisih m$\angle $A dan m$\angle $B, jika kedua sudut saling berpenyiku.
a. m$\angle $A dan m$\angle $B jika keduanya saling berpelurus. b. Selisih m$\angle $A dan m$\angle $B, jika kedua sudut saling berpenyiku.
Penyelesaian :
a). Keduanya saling berpelurus, jumlahnya $ 180^\circ $
$ \begin{align} m\angle A + m \angle B & = 180^\circ \\ \frac{2}{3} m \angle B + m \angle B & = 180^\circ \\ \frac{2}{3} m \angle B + \frac{3}{3} m \angle B & = 180^\circ \\ \frac{5}{3} m \angle B & = 180^\circ \\ m \angle B & = 180^\circ . \frac{3}{5} \\ m \angle B & = 108^\circ \end{align} $
Sehingga sudut A :
$ m\angle A = \frac{2}{3} m \angle B = \frac{2}{3} . 108^\circ = 72^\circ $
Jadi, besarnya $ m \angle A = 72^\circ \, $ dan $ m \angle B = 108^\circ $ .
b). Keduanya saling berpenyiku, jumlahnya $ 90^\circ $
$ \begin{align} m\angle A + m \angle B & = 90^\circ \\ \frac{2}{3} m \angle B + m \angle B & = 90^\circ \\ \frac{2}{3} m \angle B + \frac{3}{3} m \angle B & = 90^\circ \\ \frac{5}{3} m \angle B & = 90^\circ \\ m \angle B & = 90^\circ . \frac{3}{5} \\ m \angle B & = 54^\circ \end{align} $
Sehingga sudut A :
$ m\angle A = \frac{2}{3} m \angle B = \frac{2}{3} . 54^\circ = 36^\circ $
Selisih kedua sudut : selisih $ = 54^\circ - 36^\circ = 18^\circ $
Jadi, selisih kedua sudut adalah $ \, 18^\circ $ .
a). Keduanya saling berpelurus, jumlahnya $ 180^\circ $
$ \begin{align} m\angle A + m \angle B & = 180^\circ \\ \frac{2}{3} m \angle B + m \angle B & = 180^\circ \\ \frac{2}{3} m \angle B + \frac{3}{3} m \angle B & = 180^\circ \\ \frac{5}{3} m \angle B & = 180^\circ \\ m \angle B & = 180^\circ . \frac{3}{5} \\ m \angle B & = 108^\circ \end{align} $
Sehingga sudut A :
$ m\angle A = \frac{2}{3} m \angle B = \frac{2}{3} . 108^\circ = 72^\circ $
Jadi, besarnya $ m \angle A = 72^\circ \, $ dan $ m \angle B = 108^\circ $ .
b). Keduanya saling berpenyiku, jumlahnya $ 90^\circ $
$ \begin{align} m\angle A + m \angle B & = 90^\circ \\ \frac{2}{3} m \angle B + m \angle B & = 90^\circ \\ \frac{2}{3} m \angle B + \frac{3}{3} m \angle B & = 90^\circ \\ \frac{5}{3} m \angle B & = 90^\circ \\ m \angle B & = 90^\circ . \frac{3}{5} \\ m \angle B & = 54^\circ \end{align} $
Sehingga sudut A :
$ m\angle A = \frac{2}{3} m \angle B = \frac{2}{3} . 54^\circ = 36^\circ $
Selisih kedua sudut : selisih $ = 54^\circ - 36^\circ = 18^\circ $
Jadi, selisih kedua sudut adalah $ \, 18^\circ $ .
Soal 5.
Jika m$\angle $A - m$\angle $B = 70$^\circ $, dan m$\angle $A adalah tiga kali m$\angle $B. Hitunglah.
a. m$\angle $A + m$\angle $B.
b. Pelurus sudut A.
a. m$\angle $A + m$\angle $B.
b. Pelurus sudut A.
Penyelesaian :
*). Menyusun persamaan :
$ m \angle A - m \angle B = 70^\circ \, $ ....pers(i)
$ m \angle A = 3 m \angle B \, $ ....pers(ii)
*). Substitusi pers (ii) ke pers(i)
$ \begin{align} m \angle A - m \angle B & = 70^\circ \\ 3 m \angle B - m \angle B & = 70^\circ \\ 2 m \angle B & = 70^\circ \\ m \angle B & = \frac{70^\circ }{2} = 35^\circ \end{align} $
Sehinga sudut A : $ m \angle A = 3 m \angle B = 3 . 35^\circ = 105^\circ $
a). Nilai $ m \angle A + m \angle B = 105^\circ + 35^\circ = 140^\circ $
Jadi, nilai $ m \angle A + m \angle B = 140^\circ $
b). Pelusur sudut A $ = 180^\circ - m \angle A = 180^\circ - 105^\circ = 75^\circ $
Jadi, pelurusnya sudut A adalah $ 75^\circ $ .
*). Menyusun persamaan :
$ m \angle A - m \angle B = 70^\circ \, $ ....pers(i)
$ m \angle A = 3 m \angle B \, $ ....pers(ii)
*). Substitusi pers (ii) ke pers(i)
$ \begin{align} m \angle A - m \angle B & = 70^\circ \\ 3 m \angle B - m \angle B & = 70^\circ \\ 2 m \angle B & = 70^\circ \\ m \angle B & = \frac{70^\circ }{2} = 35^\circ \end{align} $
Sehinga sudut A : $ m \angle A = 3 m \angle B = 3 . 35^\circ = 105^\circ $
a). Nilai $ m \angle A + m \angle B = 105^\circ + 35^\circ = 140^\circ $
Jadi, nilai $ m \angle A + m \angle B = 140^\circ $
b). Pelusur sudut A $ = 180^\circ - m \angle A = 180^\circ - 105^\circ = 75^\circ $
Jadi, pelurusnya sudut A adalah $ 75^\circ $ .
Soal 6.
Perhatikan gambar di bawah ini. Sebutkanlah pasangan:
a. Sudut-sudut sehadap.
b. Sudut-sudut sepihak (dalam dan luar ).
c. Sudut-sudut berseberangan (dalam dan luar)
a. Sudut-sudut sehadap.
b. Sudut-sudut sepihak (dalam dan luar ).
c. Sudut-sudut berseberangan (dalam dan luar)
Penyelesaian :
a). Daftar pasangan sudut-sudut yang sehadap :
$ A_1 $ sehadap $ B_1 $ ; $ A_2 $ sehadap $ B_2 $ ; $ A_3 $ sehadap $ B_3 $ ; $ A_4 $ sehadap $ B_4 $
$ A_1 $ sehadap $ D_1 $ ; $ A_2 $ sehadap $ D_2 $ ; $ A_3 $ sehadap $ D_3 $ ; $ A_4 $ sehadap $ D_4 $
$ B_1 $ sehadap $ C_1 $ ; $ B_2 $ sehadap $ C_2 $ ; $ B_3 $ sehadap $ C_3 $ ; $ B_4 $ sehadap $ C_4 $
$ D_1 $ sehadap $ C_1 $ ; $ D_2 $ sehadap $ C_2 $ ; $ D_3 $ sehadap $ C_3 $ ; $ D_4 $ sehadap $ C_4 $
b). Sudut-sudut sepihak :
Sudut-sudut dalam sepihak :
$ A_2 $ sepihak $ B_1 $ ; $ A_3 $ sepihak $ B_4 $ ; $ A_4 $ sepihak $ D_1 $ ; $ A_3 $ sepihak $ D_2 $
$ B_4 $ sepihak $ C_1 $ ; $ B_3 $ sepihak $ C_2 $ ; $ C_4 $ sepihak $ D_3 $ ; $ C_1 $ sepihak $ D_2 $
Sudut-sudut luar sepihak :
$ A_1 $ sepihak $ B_2 $ ; $ A_4 $ sepihak $ B_3 $ ; $ A_1 $ sepihak $ D_4 $ ; $ A_2 $ sepihak $ D_3 $
$ B_1 $ sepihak $ C_4 $ ; $ B_2 $ sepihak $ C_3 $ ; $ C_3 $ sepihak $ D_4 $ ; $ C_2 $ sepihak $ D_1 $
c). Sudut-sudut bersebrangan :
Sudut-sudut dalam bersebrangan :
$ A_2 $ dan $ B_4 $ ; $ A_3 $ dan $ B_1 $ ; $ A_4 $ dan $ D_2 $ ; $ A_3 $ dan $ D_1 $
$ B_4 $ dan $ C_2 $ ; $ B_3 $ dan $ C_1 $ ; $ C_4 $ dan $ D_2 $ ; $ C_1 $ dan $ D_3 $
Sudut-sudut luar bersebrangan :
$ A_1 $ dan $ B_3 $ ; $ A_4 $ dan $ B_2 $ ; $ A_1 $ dan $ D_3 $ ; $ A_2 $ dan $ D_4 $
$ B_1 $ dan $ C_3 $ ; $ B_2 $ dan $ C_4 $ ; $ C_3 $ dan $ D_1 $ ; $ C_2 $ dan $ D_4 $
a). Daftar pasangan sudut-sudut yang sehadap :
$ A_1 $ sehadap $ B_1 $ ; $ A_2 $ sehadap $ B_2 $ ; $ A_3 $ sehadap $ B_3 $ ; $ A_4 $ sehadap $ B_4 $
$ A_1 $ sehadap $ D_1 $ ; $ A_2 $ sehadap $ D_2 $ ; $ A_3 $ sehadap $ D_3 $ ; $ A_4 $ sehadap $ D_4 $
$ B_1 $ sehadap $ C_1 $ ; $ B_2 $ sehadap $ C_2 $ ; $ B_3 $ sehadap $ C_3 $ ; $ B_4 $ sehadap $ C_4 $
$ D_1 $ sehadap $ C_1 $ ; $ D_2 $ sehadap $ C_2 $ ; $ D_3 $ sehadap $ C_3 $ ; $ D_4 $ sehadap $ C_4 $
b). Sudut-sudut sepihak :
Sudut-sudut dalam sepihak :
$ A_2 $ sepihak $ B_1 $ ; $ A_3 $ sepihak $ B_4 $ ; $ A_4 $ sepihak $ D_1 $ ; $ A_3 $ sepihak $ D_2 $
$ B_4 $ sepihak $ C_1 $ ; $ B_3 $ sepihak $ C_2 $ ; $ C_4 $ sepihak $ D_3 $ ; $ C_1 $ sepihak $ D_2 $
Sudut-sudut luar sepihak :
$ A_1 $ sepihak $ B_2 $ ; $ A_4 $ sepihak $ B_3 $ ; $ A_1 $ sepihak $ D_4 $ ; $ A_2 $ sepihak $ D_3 $
$ B_1 $ sepihak $ C_4 $ ; $ B_2 $ sepihak $ C_3 $ ; $ C_3 $ sepihak $ D_4 $ ; $ C_2 $ sepihak $ D_1 $
c). Sudut-sudut bersebrangan :
Sudut-sudut dalam bersebrangan :
$ A_2 $ dan $ B_4 $ ; $ A_3 $ dan $ B_1 $ ; $ A_4 $ dan $ D_2 $ ; $ A_3 $ dan $ D_1 $
$ B_4 $ dan $ C_2 $ ; $ B_3 $ dan $ C_1 $ ; $ C_4 $ dan $ D_2 $ ; $ C_1 $ dan $ D_3 $
Sudut-sudut luar bersebrangan :
$ A_1 $ dan $ B_3 $ ; $ A_4 $ dan $ B_2 $ ; $ A_1 $ dan $ D_3 $ ; $ A_2 $ dan $ D_4 $
$ B_1 $ dan $ C_3 $ ; $ B_2 $ dan $ C_4 $ ; $ C_3 $ dan $ D_1 $ ; $ C_2 $ dan $ D_4 $
Soal 7.
Perhatikan gambar di bawah ini. Tentukan besar sudut
a. $ \angle $ABC
b. $ \angle $ACB
c. $ \angle $ACG
d. $ \angle $FGC
a. $ \angle $ABC
b. $ \angle $ACB
c. $ \angle $ACG
d. $ \angle $FGC
Penyelesaian :
a). Sudut ABC dan sudut ABD berpelurus, jumlahnya $ 180^\circ $
$ \angle ABC + \angle ABD = 180^\circ $
$ \angle ABC = 180^\circ - \angle ABD = 180^\circ - 120^\circ = 60^\circ $
Jadi, besar sudut ABC adalah $ 60^\circ $ .
b). sudut A, B, dan C adalah sudut pada segitiga, jumlahnya $ 180^\circ $
$ \begin{align} \angle ACB + \angle ABC + \angle BAC & = 180^\circ \\ \angle ACB + 60^\circ + 55^\circ & = 180^\circ \\ \angle ACB + 115^\circ & = 180^\circ \\ \angle ACB & = 180^\circ - 115^\circ \\ \angle ACB & = 75^\circ \end{align} $
Jadi, besar sudut ACB adalah $ 75^\circ $ .
c). Sudut ACG dan sudut ACB berpelurus, jumlahnya $ 180^\circ $
$ \angle ACG + \angle ACB = 180^\circ $
$ \angle ACG = 180^\circ - \angle ACB = 180^\circ - 75^\circ = 115^\circ $
Jadi, besar sudut ACG adalah $ 115^\circ $ .
d). Sudut FGC bertolak belakang dengan sudut ACB, besarnya sama,
Sehingga $ \angle FGC = \angle ACB = 75^\circ $
Jadi, besar sudut FGC adalah $ 75^\circ $ .
a). Sudut ABC dan sudut ABD berpelurus, jumlahnya $ 180^\circ $
$ \angle ABC + \angle ABD = 180^\circ $
$ \angle ABC = 180^\circ - \angle ABD = 180^\circ - 120^\circ = 60^\circ $
Jadi, besar sudut ABC adalah $ 60^\circ $ .
b). sudut A, B, dan C adalah sudut pada segitiga, jumlahnya $ 180^\circ $
$ \begin{align} \angle ACB + \angle ABC + \angle BAC & = 180^\circ \\ \angle ACB + 60^\circ + 55^\circ & = 180^\circ \\ \angle ACB + 115^\circ & = 180^\circ \\ \angle ACB & = 180^\circ - 115^\circ \\ \angle ACB & = 75^\circ \end{align} $
Jadi, besar sudut ACB adalah $ 75^\circ $ .
c). Sudut ACG dan sudut ACB berpelurus, jumlahnya $ 180^\circ $
$ \angle ACG + \angle ACB = 180^\circ $
$ \angle ACG = 180^\circ - \angle ACB = 180^\circ - 75^\circ = 115^\circ $
Jadi, besar sudut ACG adalah $ 115^\circ $ .
d). Sudut FGC bertolak belakang dengan sudut ACB, besarnya sama,
Sehingga $ \angle FGC = \angle ACB = 75^\circ $
Jadi, besar sudut FGC adalah $ 75^\circ $ .
Soal 8.
Sudut P dan sudut Q adalah sudut dalam sepihak. m$\angle $ Q = 112$^\circ $. Tentukanlah
m$\angle $P.
Penyelesaian :
*). Sudut dalam sepihak memiliki jumlah $ 180^\circ $
$ \angle P + \angle Q = 180^\circ \rightarrow \angle P = 180^\circ - \angle Q $
$ \angle P = 180^\circ - 112^\circ = 68^\circ $
Jadi, besarnya sudut P adalah $ 68^\circ $
*). Sudut dalam sepihak memiliki jumlah $ 180^\circ $
$ \angle P + \angle Q = 180^\circ \rightarrow \angle P = 180^\circ - \angle Q $
$ \angle P = 180^\circ - 112^\circ = 68^\circ $
Jadi, besarnya sudut P adalah $ 68^\circ $
Soal 9.
Penyelesaian :
*). Perhatikan gambar berikut,
*). Perhatikan sudut $ a , \, b , \, $ dan $ \, c \, $ adalah tiga sudut yang sehadap. Karena sudutnya sehadap, maka besarnya sama ($ a = b = c $) , sehingga $ c = 2x + 40 $ .
*). Perhatikan sudut $ c \, $ dan sudut $ x + 80 \, $ , adalah bertolak belakang, sehingga besar sudutnya juga sama.
$ \begin{align} c & = x + 80 \\ 2x + 40 & = x + 80 \\ 2x - x & = 80 - 40 \\ x & = 40 \end{align} $
Jadi, besarnya $ x \, $ adalah $ 40 $
*). Perhatikan gambar berikut,
*). Perhatikan sudut $ a , \, b , \, $ dan $ \, c \, $ adalah tiga sudut yang sehadap. Karena sudutnya sehadap, maka besarnya sama ($ a = b = c $) , sehingga $ c = 2x + 40 $ .
*). Perhatikan sudut $ c \, $ dan sudut $ x + 80 \, $ , adalah bertolak belakang, sehingga besar sudutnya juga sama.
$ \begin{align} c & = x + 80 \\ 2x + 40 & = x + 80 \\ 2x - x & = 80 - 40 \\ x & = 40 \end{align} $
Jadi, besarnya $ x \, $ adalah $ 40 $
Demikian Pembahasan Latihan 4.2 Garis dan sudut kelas VII Kurikulum 2013. Jika ada kekeliruan dalam penyelesaiannya, mohon kritik dan saranya agar penyelesaiannya menjadi lebih baik dengan memberikan komentar di kotak komentar di bawah. Semoga pembahasannya bisa bermanfaat untuk kita semua. Terima kasih.