Blog Koma - Ukuran Sudut merupakan besaran yang digunakan dalam pengukuran sudut. Dalam trigonometri ,
sudut merupakan hal yang sangat penting yang akan langsung berhubungan dengan nilai trigonometrinya (sin, cos, tan, sec, cossec, dan cot).
Pada umumnya, ada dua ukuran yang digunakan untuk menentukan besar suatu
sudut, yaitu derajat dan radian. Tanda "$\circ$" dan "rad" berturut-turut menyatakan simbol
derajat dan radian. Singkatnya, satu putaran penuh = $360^\circ$ .
$1^\circ $ didefinisikan sebagai besar sudut yang dibentuk oleh $ \frac{1}{360} \, $ putaran penuh.
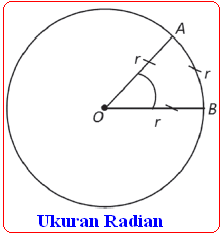
Satu radian diartikan sebagai ukuran sudut pusat $\alpha $ suatu
lingkaran yang panjang busurnya sama dengan jari-jari.
Hubungan satuan derajat dengan satuan radian, bahwa 1 putaran penuh
sama dengan $ 2\pi , rad $. Seperti dinyatakan dalam definisi berikut
Contoh :
1). Selesaikan bentuk berikut :
a). Tentukan besarnya radian dan banyak putaran jika diketahui besar sudutnya $ 150^\circ $
b). Tentukan besarnya derajat dan banyak putaran jika diketahui besar radiannya $ \frac{3}{2} \pi \, rad $
c). Tentukan besarnya derajat dan radian jika diketahui banyak putaran $ \frac{1}{3} \, $ putaran.
Penyelesaian :
a). $ 150^\circ = ... \, rad = \, ... \, $ putaran
Diketahui $ D = 150^\circ $
*). Menentukan nilai radian :
$ \begin{align} \frac{R}{D} & = \frac{\pi}{180^\circ} \\ \frac{R}{150^\circ} & = \frac{\pi}{180^\circ} \\ R & = \frac{\pi}{180^\circ} \times 150^\circ \, \, \, rad \\ R & = \frac{5}{6} \pi rad \end{align} $
*). Menentukan banyak putaran
$ \begin{align} D & = P \times 360^\circ \\ P & = \frac{D}{360^\circ} \, \, \, \text{putaran} \\ P & = \frac{150^\circ}{360^\circ} \, \, \, \text{putaran} \\ P & = \frac{5}{12} \, \, \, \text{putaran} \end{align} $
Jadi, diperoleh : $ 150^\circ = \frac{5}{6} \, rad = \, \frac{5}{12} \, $ putaran
b). $ \frac{3}{2} \pi \, rad = ... ^\circ = \, ... \, $ putaran
Diketahui $ R = \frac{3}{2} \pi \, rad $
*). Menentukan nilai derajat :
$ \begin{align} \frac{R}{D} & = \frac{\pi}{180^\circ} \\ \frac{\frac{3}{2} \pi }{D} & = \frac{\pi}{180^\circ} \\ D & = \frac{3}{2} \times 180^\circ \\ D & = 270^\circ \end{align} $
*). Menentukan banyak putaran
$ \begin{align} \frac{R}{P \times 360^\circ } & = \frac{\pi}{180^\circ} \\ \frac{\frac{3}{2} \pi }{P \times 360^\circ } & = \frac{\pi}{180^\circ} \\ \frac{\frac{3}{2} }{P \times 2 } & = \frac{1}{1} \\ P & = \frac{3}{4} \, \, \, \text{putaran} \end{align} $
Jadi, diperoleh : $ \frac{3}{2} \pi \, rad = 270 ^\circ = \, \frac{3}{4} \, $ putaran
c). $ \frac{1}{3} \, \, \, \text{putaran} = ... ^\circ = \, ... \, rad $
Diketahui $ P = \frac{1}{3} \, \, $ putaran
*). Menentukan nilai radian
$ \begin{align} \frac{R}{P \times 360^\circ } & = \frac{\pi}{180^\circ} \\ \frac{R}{P \times 2 } & = \frac{\pi}{1} \\ \frac{R}{\frac{1}{3} \times 2 } & = \pi \\ R & = \frac{2}{3}\pi \, rad \end{align} $
*). Menentukan nilai derajat
$ \begin{align} D & = P \times 360^\circ \\ D & = \frac{1}{3} \times 360^\circ \\ D & = 120^\circ \end{align} $
Jadi, diperoleh : $ \frac{1}{3} \, \, \, \text{putaran} = 120 ^\circ = \, \frac{2}{3}\pi \, rad $
2). Berapa radian sudut yang dibentuk jarum jam pada pukul 11.00?
Penyelesaian :
Sudut yang terbentuk pada pukul 11.00 adalah 30$^\circ \, \, (D = 30^\circ ) $
*). Menentukan nilai radian
$ \begin{align} \frac{R}{D} & = \frac{\pi}{180^\circ} \\ \frac{R}{30^\circ} & = \frac{\pi}{180^\circ} \\ R & = \frac{\pi}{180^\circ} \times 30^\circ \, \, \, rad \\ R & = \frac{1}{6} \pi \, rad \end{align} $
Jadi, besarnya radian yang terbentuka adalah $ \frac{1}{6} \pi \, rad $
3). Jika suatu alat pemancar berputar 60 putaran dalam setiap menit, maka tentukanlah banyak putaran dalam satu detik.?
Penyelesaian :
*). Diketahui
1 menit ada 60 putaran,
1 menit = 60 detik,
*). Menentukan putaran setiap detik :
$\begin{align} \frac{\text{putaran tiap detik}}{\text{putaran tiap menit} } & = \frac{1 \, \text{detik} }{1 \, \text{menit} } \\ \frac{\text{putaran tiap detik}}{\text{putaran tiap menit} } & = \frac{1 \, \text{detik} }{60 \, \text{detik} } \\ \frac{\text{putaran tiap detik}}{\text{60} \, \text{putaran} } & = \frac{1}{60} \\ \text{putaran tiap detik} & = \frac{1}{60} \times 60 \, \text{putaran} \\ \text{putaran tiap detik} & = 1 \, \text{putaran} \end{align} $
Jadi, tiap detik ada 1 putaran
Contoh :
1). Tentukan besar sudut koterminal dari sudut-sudut berikut :
a). $ A = 60^\circ $
b). $ B = 150^\circ $
C). $ C = 240^\circ $
Penyelesaian :
Misalkan sudut koterminalnya adalah sudut K,
*). Menentukan besarnya sudut K.
a). $ A = 60^\circ $
$ A + K = 360^\circ \rightarrow 60^\circ + K = 360^\circ \rightarrow K = 300^\circ $
b). $ B = 150^\circ $
$ B + K = 360^\circ \rightarrow 150^\circ + K = 360^\circ \rightarrow K = 210^\circ $
c). $ C = 240^\circ $
$ C + K = 360^\circ \rightarrow 240^\circ + K = 360^\circ \rightarrow K = 120^\circ $
2). Gambarkanlah sudut-sudut standar di bawah ini, dan tentukan posisi setiap sudut pada koordinat kartesius.
a) 60$^\circ$ b) -45$^\circ$ c) 120$^\circ$ d) 600$^\circ$
Penyelesaian :
Contoh :
1). Ubahlah bentuk derajat berikut dalam bentuk menit dan detik!
a). $ 62,4^\circ $
b). $ 29,23^\circ $
Penyelesaian :
a). $ 62,4^\circ = 62^\circ + 0,4(60^\prime) = 62^\circ + 24^\prime = 62^\circ 24^\prime $
b). $ 29,23^\circ $
$ \begin{align} 29,23^\circ & = 29^\circ + 0,23(60^\prime) = 29^\circ + 13,8^\prime \\ & = 29^\circ + 13^\prime + 0,8(60^{\prime \prime}) \\ & = 29^\circ + 13^\prime + 48^{\prime \prime} \\ & = 29^\circ 13^\prime 48^{\prime \prime} \end{align} $
2). Ubahlah bentuk berikut dalam derajat!
a). $ 78^\circ 30^\prime $
b). $ 58^\circ 22^\prime 16^{\prime \prime} $
Penyelesaian :
a). $ 78^\circ 30^\prime = 78^\circ + \frac{30^\circ}{60} = 78^\circ + 0,5^\circ = 78,5^\circ $
b). $ 58^\circ 22^\prime 16^{\prime \prime} = 58^\circ + \frac{22^\circ}{60} + \frac{16^\circ}{3600} = 58,37111...^\circ = 58,37^\circ $
3). Hitunglah operasi berikut!
a). $ 25^\circ 15^\prime + 62^\circ 56^\prime $
b). $ 35^\circ 55^\prime + 62^\circ 2^\prime 26^{\prime \prime} $
c). $ 63^\circ 55^\prime - 23^\circ 15^\prime $
d). $ 37^\circ 42^\prime - 20^\circ 31^\prime 26^{\prime \prime} $
e). $ 32^\circ 25^\prime - 21^\circ 35^\prime 14^{\prime \prime} $
Penyelesaian :
a). $ 25^\circ 15^\prime + 62^\circ 56^\prime $
$\begin{array}{cc} 25^\circ 15^\prime & \\ 62^\circ 56^\prime & + \\ \hline 87^\circ 71^\prime & \end{array} $
jadi, $ 25^\circ 15^\prime + 62^\circ 56^\prime = 87^\circ 71^\prime = 87^\circ + 60^\prime + 11^\prime = 87^\circ + 1^\circ + 11^\prime = 88^\circ 11^\prime $
b). $ 35^\circ 55^\prime + 62^\circ 2^\prime 26^{\prime \prime} $
$\begin{array}{cc} 35^\circ 55^\prime & \\ 62^\circ 2^\prime 26^{\prime \prime} & + \\ \hline 97^\circ 57^\prime 26^{\prime \prime} & \end{array} $
jadi, $ 35^\circ 55^\prime + 62^\circ 2^\prime 26^{\prime \prime} = 97^\circ 57^\prime 26^{\prime \prime} $
c). $ 63^\circ 55^\prime - 23^\circ 15^\prime $
$\begin{array}{cc} 63^\circ 55^\prime & \\ 23^\circ 15^\prime & - \\ \hline 40^\circ 40^\prime & \end{array} $
jadi, $ 63^\circ 55^\prime - 23^\circ 15^\prime = 40^\circ 40^\prime $
d). $ 37^\circ 42^\prime - 20^\circ 31^\prime 26^{\prime \prime} $
$\begin{array}{cccc} 37^\circ 42^\prime & \rightarrow & 37^\circ 41^\prime 60^{\prime \prime} & \\ 20^\circ 31^\prime 26^{\prime \prime} & \rightarrow & 20^\circ 31^\prime 26^{\prime \prime} & - \\ \hline & & 17^\circ 10^\prime 34^{\prime \prime} & & \end{array} $
jadi, $ 37^\circ 42^\prime - 20^\circ 31^\prime 26^{\prime \prime} = 17^\circ 10^\prime 34^{\prime \prime} $
e). $ 32^\circ 25^\prime - 21^\circ 35^\prime 14^{\prime \prime} $
$\begin{array}{cccccc} 32^\circ 25^\prime & \rightarrow & 32^\circ 24^\prime 60^{\prime \prime} & \rightarrow & 31^\circ 84^\prime 60^{\prime \prime} & \\ 21^\circ 35^\prime 14^{\prime \prime} & \rightarrow & 21^\circ 35^\prime 14^{\prime \prime} & \rightarrow & 21^\circ 35^\prime 14^{\prime \prime} & - \\ \hline & & & & 10^\circ 49^\prime 46^{\prime \prime} & \end{array} $
jadi, $ 32^\circ 25^\prime - 21^\circ 35^\prime 14^{\prime \prime} = 10^\circ 49^\prime 46^{\prime \prime} $
Hubungan nilai Derajat, Radian, dan Banyak Putaran
Misalkan Dejarat kita simbolkan D, Radian kita simbolkan R, dan banyak putaran kita simbolkan P, maka
hubungan Derajat, Radian, dan banyak Putaran (D, R, P), yaitu :
$ \begin{align} \frac{R}{D} = \frac{R}{P \times 360^\circ } = \frac{\pi}{180^\circ} \end{align} \, \, $ dan $ \, \, \begin{align} D = P \times 360^\circ \end{align} $
dimana, nilai $ \pi = 3,14 \, $ untuk radian dan $ \pi = 180^\circ \, $ untuk derajat.
Persamaan di atas digunakan untuk menentukan nilai satuan yang lain jika nilai salah satuan diketahui, misalkan diketahui nilai derajat, akan ditanya nilai radian dan berapa putarannya.
$ \begin{align} \frac{R}{D} = \frac{R}{P \times 360^\circ } = \frac{\pi}{180^\circ} \end{align} \, \, $ dan $ \, \, \begin{align} D = P \times 360^\circ \end{align} $
dimana, nilai $ \pi = 3,14 \, $ untuk radian dan $ \pi = 180^\circ \, $ untuk derajat.
Persamaan di atas digunakan untuk menentukan nilai satuan yang lain jika nilai salah satuan diketahui, misalkan diketahui nilai derajat, akan ditanya nilai radian dan berapa putarannya.
Contoh :
1). Selesaikan bentuk berikut :
a). Tentukan besarnya radian dan banyak putaran jika diketahui besar sudutnya $ 150^\circ $
b). Tentukan besarnya derajat dan banyak putaran jika diketahui besar radiannya $ \frac{3}{2} \pi \, rad $
c). Tentukan besarnya derajat dan radian jika diketahui banyak putaran $ \frac{1}{3} \, $ putaran.
Penyelesaian :
a). $ 150^\circ = ... \, rad = \, ... \, $ putaran
Diketahui $ D = 150^\circ $
*). Menentukan nilai radian :
$ \begin{align} \frac{R}{D} & = \frac{\pi}{180^\circ} \\ \frac{R}{150^\circ} & = \frac{\pi}{180^\circ} \\ R & = \frac{\pi}{180^\circ} \times 150^\circ \, \, \, rad \\ R & = \frac{5}{6} \pi rad \end{align} $
*). Menentukan banyak putaran
$ \begin{align} D & = P \times 360^\circ \\ P & = \frac{D}{360^\circ} \, \, \, \text{putaran} \\ P & = \frac{150^\circ}{360^\circ} \, \, \, \text{putaran} \\ P & = \frac{5}{12} \, \, \, \text{putaran} \end{align} $
Jadi, diperoleh : $ 150^\circ = \frac{5}{6} \, rad = \, \frac{5}{12} \, $ putaran
b). $ \frac{3}{2} \pi \, rad = ... ^\circ = \, ... \, $ putaran
Diketahui $ R = \frac{3}{2} \pi \, rad $
*). Menentukan nilai derajat :
$ \begin{align} \frac{R}{D} & = \frac{\pi}{180^\circ} \\ \frac{\frac{3}{2} \pi }{D} & = \frac{\pi}{180^\circ} \\ D & = \frac{3}{2} \times 180^\circ \\ D & = 270^\circ \end{align} $
*). Menentukan banyak putaran
$ \begin{align} \frac{R}{P \times 360^\circ } & = \frac{\pi}{180^\circ} \\ \frac{\frac{3}{2} \pi }{P \times 360^\circ } & = \frac{\pi}{180^\circ} \\ \frac{\frac{3}{2} }{P \times 2 } & = \frac{1}{1} \\ P & = \frac{3}{4} \, \, \, \text{putaran} \end{align} $
Jadi, diperoleh : $ \frac{3}{2} \pi \, rad = 270 ^\circ = \, \frac{3}{4} \, $ putaran
c). $ \frac{1}{3} \, \, \, \text{putaran} = ... ^\circ = \, ... \, rad $
Diketahui $ P = \frac{1}{3} \, \, $ putaran
*). Menentukan nilai radian
$ \begin{align} \frac{R}{P \times 360^\circ } & = \frac{\pi}{180^\circ} \\ \frac{R}{P \times 2 } & = \frac{\pi}{1} \\ \frac{R}{\frac{1}{3} \times 2 } & = \pi \\ R & = \frac{2}{3}\pi \, rad \end{align} $
*). Menentukan nilai derajat
$ \begin{align} D & = P \times 360^\circ \\ D & = \frac{1}{3} \times 360^\circ \\ D & = 120^\circ \end{align} $
Jadi, diperoleh : $ \frac{1}{3} \, \, \, \text{putaran} = 120 ^\circ = \, \frac{2}{3}\pi \, rad $
2). Berapa radian sudut yang dibentuk jarum jam pada pukul 11.00?
Penyelesaian :
Sudut yang terbentuk pada pukul 11.00 adalah 30$^\circ \, \, (D = 30^\circ ) $
*). Menentukan nilai radian
$ \begin{align} \frac{R}{D} & = \frac{\pi}{180^\circ} \\ \frac{R}{30^\circ} & = \frac{\pi}{180^\circ} \\ R & = \frac{\pi}{180^\circ} \times 30^\circ \, \, \, rad \\ R & = \frac{1}{6} \pi \, rad \end{align} $
Jadi, besarnya radian yang terbentuka adalah $ \frac{1}{6} \pi \, rad $
3). Jika suatu alat pemancar berputar 60 putaran dalam setiap menit, maka tentukanlah banyak putaran dalam satu detik.?
Penyelesaian :
*). Diketahui
1 menit ada 60 putaran,
1 menit = 60 detik,
*). Menentukan putaran setiap detik :
$\begin{align} \frac{\text{putaran tiap detik}}{\text{putaran tiap menit} } & = \frac{1 \, \text{detik} }{1 \, \text{menit} } \\ \frac{\text{putaran tiap detik}}{\text{putaran tiap menit} } & = \frac{1 \, \text{detik} }{60 \, \text{detik} } \\ \frac{\text{putaran tiap detik}}{\text{60} \, \text{putaran} } & = \frac{1}{60} \\ \text{putaran tiap detik} & = \frac{1}{60} \times 60 \, \text{putaran} \\ \text{putaran tiap detik} & = 1 \, \text{putaran} \end{align} $
Jadi, tiap detik ada 1 putaran
Konsep Dasar Sudut
Dalam kajian geometris, sudut didefinisikan sebagai hasil rotasi dari sisi awal
(initial side) ke sisi akhir (terminal side). Selain itu, arah putaran memiliki makna
dalam sudut. Suatu sudut bertanda "positif" jika arah putarannya berlawanan dengan
arah putaran jarum jam, dan bertanda "negatif" jika arah putarannya searah dengan
jarum jam. Arah putaran untuk membentuk sudut juga dapat diperhatikan pada posisi
sisi akhir terhadap sisi awal. Untuk memudahkannya, mari kita cermati deskripsi berikut ini.
*). Sudut standar (baku) adalah sudut sisi awal suatu garis berimpit dengan sumbu X dan sisi terminalnya terletak pada salah satu kuadran pada koordinat kartesius itu.
*). Sudut pembatas kuadran adalah sudut sisi akhir berada pada salah satu sumbu pada koordinat tersebut, yaitu $0^\circ, 90^\circ , 180^\circ , 270^\circ \, $ dan $ 360^\circ $
*). Lambang atau simbol sudut lazimnya digunakan huruf Yunani, seperti, $\alpha $ (alpha), $\beta $ (betha), $\gamma $ (gamma), dan $\theta$ (tetha), dan juga digunakan huruf-huruf kapital, seperti A, B, C, dan D.
*). Sudut-sudut koterminal adalah dua sudut standar, memiliki sisi-sisi akhir (terminal side) yang berimpit . Jika sudut yang dihasilkan sebesar $ \alpha $ (sudut standar), maka sudut $ \beta $ disebut sebagai sudut koterminal, sehingga $ \alpha + \beta = 360^\circ $ .
*). Sudut standar (baku) adalah sudut sisi awal suatu garis berimpit dengan sumbu X dan sisi terminalnya terletak pada salah satu kuadran pada koordinat kartesius itu.
*). Sudut pembatas kuadran adalah sudut sisi akhir berada pada salah satu sumbu pada koordinat tersebut, yaitu $0^\circ, 90^\circ , 180^\circ , 270^\circ \, $ dan $ 360^\circ $
*). Lambang atau simbol sudut lazimnya digunakan huruf Yunani, seperti, $\alpha $ (alpha), $\beta $ (betha), $\gamma $ (gamma), dan $\theta$ (tetha), dan juga digunakan huruf-huruf kapital, seperti A, B, C, dan D.
*). Sudut-sudut koterminal adalah dua sudut standar, memiliki sisi-sisi akhir (terminal side) yang berimpit . Jika sudut yang dihasilkan sebesar $ \alpha $ (sudut standar), maka sudut $ \beta $ disebut sebagai sudut koterminal, sehingga $ \alpha + \beta = 360^\circ $ .
1). Tentukan besar sudut koterminal dari sudut-sudut berikut :
a). $ A = 60^\circ $
b). $ B = 150^\circ $
C). $ C = 240^\circ $
Penyelesaian :
Misalkan sudut koterminalnya adalah sudut K,
*). Menentukan besarnya sudut K.
a). $ A = 60^\circ $
$ A + K = 360^\circ \rightarrow 60^\circ + K = 360^\circ \rightarrow K = 300^\circ $
b). $ B = 150^\circ $
$ B + K = 360^\circ \rightarrow 150^\circ + K = 360^\circ \rightarrow K = 210^\circ $
c). $ C = 240^\circ $
$ C + K = 360^\circ \rightarrow 240^\circ + K = 360^\circ \rightarrow K = 120^\circ $
2). Gambarkanlah sudut-sudut standar di bawah ini, dan tentukan posisi setiap sudut pada koordinat kartesius.
a) 60$^\circ$ b) -45$^\circ$ c) 120$^\circ$ d) 600$^\circ$
Penyelesaian :
Hubungan Derajat, Menit, dan Detik
Berikut hubungan derajat, menit, dan detik.
*). $ 1^\circ = 1 \, $ jam
*). $ 1^\circ = 60^\prime = 60 \, $ menit
*). $ 1^\circ = 3600^{\prime \prime} = 3600 \, $ detik
Keterangan :
$ ^\prime \, $ adalah simbol menit.
$ ^{\prime \prime} \, $ adalah simbol detik.
*). $ 1^\circ = 1 \, $ jam
*). $ 1^\circ = 60^\prime = 60 \, $ menit
*). $ 1^\circ = 3600^{\prime \prime} = 3600 \, $ detik
Keterangan :
$ ^\prime \, $ adalah simbol menit.
$ ^{\prime \prime} \, $ adalah simbol detik.
1). Ubahlah bentuk derajat berikut dalam bentuk menit dan detik!
a). $ 62,4^\circ $
b). $ 29,23^\circ $
Penyelesaian :
a). $ 62,4^\circ = 62^\circ + 0,4(60^\prime) = 62^\circ + 24^\prime = 62^\circ 24^\prime $
b). $ 29,23^\circ $
$ \begin{align} 29,23^\circ & = 29^\circ + 0,23(60^\prime) = 29^\circ + 13,8^\prime \\ & = 29^\circ + 13^\prime + 0,8(60^{\prime \prime}) \\ & = 29^\circ + 13^\prime + 48^{\prime \prime} \\ & = 29^\circ 13^\prime 48^{\prime \prime} \end{align} $
2). Ubahlah bentuk berikut dalam derajat!
a). $ 78^\circ 30^\prime $
b). $ 58^\circ 22^\prime 16^{\prime \prime} $
Penyelesaian :
a). $ 78^\circ 30^\prime = 78^\circ + \frac{30^\circ}{60} = 78^\circ + 0,5^\circ = 78,5^\circ $
b). $ 58^\circ 22^\prime 16^{\prime \prime} = 58^\circ + \frac{22^\circ}{60} + \frac{16^\circ}{3600} = 58,37111...^\circ = 58,37^\circ $
3). Hitunglah operasi berikut!
a). $ 25^\circ 15^\prime + 62^\circ 56^\prime $
b). $ 35^\circ 55^\prime + 62^\circ 2^\prime 26^{\prime \prime} $
c). $ 63^\circ 55^\prime - 23^\circ 15^\prime $
d). $ 37^\circ 42^\prime - 20^\circ 31^\prime 26^{\prime \prime} $
e). $ 32^\circ 25^\prime - 21^\circ 35^\prime 14^{\prime \prime} $
Penyelesaian :
a). $ 25^\circ 15^\prime + 62^\circ 56^\prime $
$\begin{array}{cc} 25^\circ 15^\prime & \\ 62^\circ 56^\prime & + \\ \hline 87^\circ 71^\prime & \end{array} $
jadi, $ 25^\circ 15^\prime + 62^\circ 56^\prime = 87^\circ 71^\prime = 87^\circ + 60^\prime + 11^\prime = 87^\circ + 1^\circ + 11^\prime = 88^\circ 11^\prime $
b). $ 35^\circ 55^\prime + 62^\circ 2^\prime 26^{\prime \prime} $
$\begin{array}{cc} 35^\circ 55^\prime & \\ 62^\circ 2^\prime 26^{\prime \prime} & + \\ \hline 97^\circ 57^\prime 26^{\prime \prime} & \end{array} $
jadi, $ 35^\circ 55^\prime + 62^\circ 2^\prime 26^{\prime \prime} = 97^\circ 57^\prime 26^{\prime \prime} $
c). $ 63^\circ 55^\prime - 23^\circ 15^\prime $
$\begin{array}{cc} 63^\circ 55^\prime & \\ 23^\circ 15^\prime & - \\ \hline 40^\circ 40^\prime & \end{array} $
jadi, $ 63^\circ 55^\prime - 23^\circ 15^\prime = 40^\circ 40^\prime $
d). $ 37^\circ 42^\prime - 20^\circ 31^\prime 26^{\prime \prime} $
$\begin{array}{cccc} 37^\circ 42^\prime & \rightarrow & 37^\circ 41^\prime 60^{\prime \prime} & \\ 20^\circ 31^\prime 26^{\prime \prime} & \rightarrow & 20^\circ 31^\prime 26^{\prime \prime} & - \\ \hline & & 17^\circ 10^\prime 34^{\prime \prime} & & \end{array} $
jadi, $ 37^\circ 42^\prime - 20^\circ 31^\prime 26^{\prime \prime} = 17^\circ 10^\prime 34^{\prime \prime} $
e). $ 32^\circ 25^\prime - 21^\circ 35^\prime 14^{\prime \prime} $
$\begin{array}{cccccc} 32^\circ 25^\prime & \rightarrow & 32^\circ 24^\prime 60^{\prime \prime} & \rightarrow & 31^\circ 84^\prime 60^{\prime \prime} & \\ 21^\circ 35^\prime 14^{\prime \prime} & \rightarrow & 21^\circ 35^\prime 14^{\prime \prime} & \rightarrow & 21^\circ 35^\prime 14^{\prime \prime} & - \\ \hline & & & & 10^\circ 49^\prime 46^{\prime \prime} & \end{array} $
jadi, $ 32^\circ 25^\prime - 21^\circ 35^\prime 14^{\prime \prime} = 10^\circ 49^\prime 46^{\prime \prime} $