Penjabaran Kedudukan Dua Lingkaran
Jika terdapat dua lingkaran masing-masing lingkaran $L_1 $
berpusat di $ P $ dengan jari-jari $ R $ dan lingkaran $ L_2 $ berpusat di $ Q $ dengan jari-jari $ r $ di mana $ R > r $ maka terdapat beberapa kedudukan
lingkaran sebagai berikut.
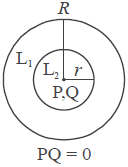
i). $L_2$ terletak di dalam $L_1$ dengan $P$ dan $Q$ berimpit, Syarat : $PQ = 0$. Dalam hal ini dikatakan $L_2$ terletak di dalam $L_1$ dan konsentris (sepusat).
ii). $L_2 $ terletak di dalam $L_1$ , syarat : $ PQ < r < R $ atau $ PQ < R - r $. Dalam hal ini dikatakan $L_2 $ terletak di dalam $ L_1 $ yang disebut juaga tidak konsentris.
iii). $L_1$ dan $L_2 $ bersinggungan di dalam, syaratnya : $ PQ = R - r $
iv). $L_1 $ berpotongan dengan $L_2 $ , syaratnya : $ R - r < PQ < R + r. $
v). $L_1$ dan $L_2 $ bersinggungan di luar, syaratnya : $ PQ = R + r $
vi). $L_1$ terletak di luar $L_2$ , syaratnya : $ PQ > R + r $, sehingga $L_1 $ dan $L_2$ saling terpisah.
vii). $L_1$ ortogonal (tegak lurus) $L_2$ , syaratnya : $ PQ^2 = R^2 + r^2 $ .
viii). $L_1$ berpotongan $L_2$ tepat pada diameter salah satu lingkaran (membagi dua bagian sama besar yaitu diameter garis warna merah), syaratnya : $ PQ^2 = R^2 - r^2 $ .
Keterangan : $ PQ = \, $ jarak titik $ P \, $ dan $ Q $.
i). $L_2$ terletak di dalam $L_1$ dengan $P$ dan $Q$ berimpit, Syarat : $PQ = 0$. Dalam hal ini dikatakan $L_2$ terletak di dalam $L_1$ dan konsentris (sepusat).
ii). $L_2 $ terletak di dalam $L_1$ , syarat : $ PQ < r < R $ atau $ PQ < R - r $. Dalam hal ini dikatakan $L_2 $ terletak di dalam $ L_1 $ yang disebut juaga tidak konsentris.
iii). $L_1$ dan $L_2 $ bersinggungan di dalam, syaratnya : $ PQ = R - r $
iv). $L_1 $ berpotongan dengan $L_2 $ , syaratnya : $ R - r < PQ < R + r. $
vi). $L_1$ terletak di luar $L_2$ , syaratnya : $ PQ > R + r $, sehingga $L_1 $ dan $L_2$ saling terpisah.
vii). $L_1$ ortogonal (tegak lurus) $L_2$ , syaratnya : $ PQ^2 = R^2 + r^2 $ .
viii). $L_1$ berpotongan $L_2$ tepat pada diameter salah satu lingkaran (membagi dua bagian sama besar yaitu diameter garis warna merah), syaratnya : $ PQ^2 = R^2 - r^2 $ .
Keterangan : $ PQ = \, $ jarak titik $ P \, $ dan $ Q $.
Contoh :
1). Tentukan kedudukan lingkaran $ L_1 : (x-1)^2 + (y+3)^2 = 25 \, $ dan linkaran $ L_2 : (x+ 2)^2 + (y -1)^2 = 9 $.
Penyelesaian :
*). Menentukan jari-jari dan pusat masing-masing lingkaran.
$ L_1 : (x-1)^2 + (y+3)^2 = 25 $
Jari-jari : $ r^2 = 25 \rightarrow r = 5 \, $ sebagai $ R = 5 $
Pusat lingkaran : $ A (a,b) = A(1,-3) $
$ L_2 : (x+ 2)^2 + (y -1)^2 = 9 $
Jari-jari : $ r^2 = 9 \rightarrow r = 3 $
Pusat lingkaran : $ B (a,b) = B(-2,1) $
*). Jarak titik pusat kedua lingkaran : $ AB $
jarak titik A(1,-3) dan B(-2,1)
$ AB = \sqrt{(-2-1)^2 + (1-(-3))^2} = \sqrt{9 + 16} = \sqrt{25} = 5 $
*). Cek kedudukan kedua lingkaran, $ AB = 5, \, R = 5, \, r = 3 $
$ AB = 0 \, $ (tidak memenuhi)
$ AB < r < R \, $ (tidak memenuhi)
$ AB = R - r \, $ (tidak memenuhi)
$ R - r < AB < R + r \, $ (memenuhi)
$ AB = R + r \, $ (tidak memenuhi)
$ AB > R + r \, $ (tidak memenuhi)
$ AB^2 = R^2 + r^2 \, $ (tidak memenuhi)
$ AB^2 = R^2 - r^2 \, $ (tidak memenuhi)
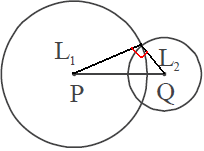
Karena yang memenuhi $ R - r < AB < R + r \, $ , maka kedua lingkaran berpotongan.!
Untuk lebih jelasanya, berikut gambar kedua lingkarannya :
Untuk lebih memantapkan pemahaman tentang kedudukan dua lingkaran, sebaiknya teman-teman juga membaca artikel "variasi soal kedudukan dua lingkaran".
Menentukan titik potong atau titik singgung dua lingkaran
Langkah-langkah menentukan titik potong atau titik singgung kedua lingkaran, yaitu :
*). Eliminasi kedua persamaan lingkaran sehingga terbentuk persamaan garis.
*). Substitusi persamaan garis yang ada ke salah satu lingkaran, lalu tentukan nilai $ x \, $ dan $ y $ .
*). Eliminasi kedua persamaan lingkaran sehingga terbentuk persamaan garis.
*). Substitusi persamaan garis yang ada ke salah satu lingkaran, lalu tentukan nilai $ x \, $ dan $ y $ .
2). Tentukan titik potong kedua lingkaran pada soal nomor 1 di atas.
Penyelesaian :
*). Menjabarkan kedua persamaan lingkaran.
$ L_1 : (x-1)^2 + (y+3)^2 = 25 \rightarrow x^2 + y^2 - 2x + 6y = 15 $
$ L_2 : (x+ 2)^2 + (y -1)^2 = 9 \rightarrow x^2 + y^2 + 4x + -2y = 4 $
*). Eliminasi kedua persamaan lingkaran ,
$ \begin{array}{cc} x^2 + y^2 - 2x + 6y = 15 & \\ x^2 + y^2 + 4x + -2y = 4 & - \\ \hline -6y + 8y = 11 & \end{array} $
*). Substitusi garis ke lingkaran kedua
$ -6x + 8y = 11 \rightarrow y = \frac{1}{8}(11 + 6x) $
$\begin{align} x^2 + y^2 + 4x + -2y & = 4 \\ x^2 + [\frac{1}{8}(11 + 6x)]^2 + 4x + -2[\frac{1}{8}(11 + 6x)] & = 4 \\ x^2 + \frac{1}{64}(36x^2 + 132x + 121) + 4x -\frac{2}{8}(11 + 6x) & = 4 \, \, \, \, \text{(kali 64)} \\ 64x^2 + (36x^2 + 132x + 121) + 256x -16(11 + 6x) & = 256 \\ 64x^2 + (36x^2 + 132x + 121) + 256x -171 - 96x & = 256 \\ 100x^2 + 292x - 306 & = 0 \, \, \, \, \text{(bagi 2)} \\ 50x^2 + 146x - 153 & = 0 \\ a = 50, \, b = 146, \, c & = -153 \end{align} $
Gunakan rumus ABC : $ x = \frac{-b \pm \sqrt{b^2 - 4.a.c}}{2a} \, $ pada persamaan kuadrat.
$\begin{align} 50x^2 + 146x - 153 & = 0 \\ a = 50, \, b = 146, \, c & = -153 \\ x & = \frac{-b \pm \sqrt{b^2 - 4.a.c}}{2a} \\ x & = \frac{-146 \pm \sqrt{146^2 - 4.50.(-153)}}{2.50} \\ x & = \frac{-146 \pm \sqrt{51916}}{100} \\ x & = \frac{-146 \pm 227,8}{100} \\ x & = \frac{81,8}{100} \\ x_1 & = 0,818 = 0,8 \\ x & = \frac{-146 - 227,8}{100} \\ x & = \frac{-373,8}{100} \\ x_2 & = -3,738 = -3,7 \end{align} $
*). Substitusi nilai $ x $ ke persamaan garis $ y = \frac{1}{8}(11 + 6x) $
$ x_1 = 0,8 \rightarrow y_1 = \frac{1}{8}(11 + 6x) = \frac{1}{8}(11 + 6(0,8)) = 1,98 $
$ x_2 = -3,7 \rightarrow y_2 = \frac{1}{8}(11 + 6x) = \frac{1}{8}(11 + 6(-3,7)) = -1,4 $
Jadi, titik potong kedua lingkaran adalah (0.8 , 1.98) dan (-3.7 , -1.4).