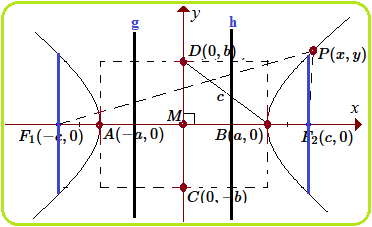
Perhatikan ilustrasi kurva Hiperbola dan unsur-unsurnya berikut ini.
Unsur-unsur dari kurva Hiperbola di atas yaitu :
*). Titik $ P(x,y) $ adalah titik sembarang pada Hiperbola sehingga berlaku $ |F_1P| - |F_2P| = 2a $
*). Titik pusat Hiperbola : $ M(0,0) $
*). Titik fokus Hiperbola : $ F_1(-c,0) $ dan $ F_2(c,0) $
*). Sumbu Simetri :
-). Sumbu utama, yaitu sumbu X.
-). Sumbu sekawan, yaitu sumbu Y.
*). Sumbu nyata, yaitu $ AB = 2a $ .
*). Sumbu imajiner, yaitu $ CD = 2b $ .
*). Titik puncak Hiperbola, yaitu titik $ A(-a.0) $ dan $ B(a,0) $ adalah titik potong Hiperbola dengan sumbu nyata
*). Latus rectum adalah garis melalui titik fokus $ F_1 $ dan $ F_2 $ yang tegak lurus dengan sumbu nyata. Pada gambar, garis latus rectumnya adalah garis warna birus. Panjang latus rectum $ = \frac{2b^2}{a} $.
*). Hubungan $ a, b$ , dan $ c $ adalah berlaku pythagoras yaitu $ c^2 = a^2 + b^2 $ pada segitiga $ DMB $.
*). Eksentrisitas $(e)$ adalah perbandingan jarak dua titik fokus dan panjang sumbu nyatanya, sehingga dapat kita tulis rumusnya : $ e = \frac{c}{a} $.
*). Direktris adalah sebuah garis yang tegak lurus dengan sumbu nyata yang ditunjukkan oleh garis $ g $ dan gris $ h $. Persamaan direktris masing-masing : garis $ g $ adalah $ x = -\frac{a^2}{c} $ dan garis $ h $ adalah $ x = \frac{a^2}{c} $.
*). Adapun persamaan Hiperbola yang sesuai dengan ilustrasi di atas adalah $ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $.
Sesuai dengan sumbu nyata dan titik pusat, Persamaan Hiperbola dan Unsur-unsurnya dibagi menjadi empat bagian yaitu :
1). Persamaan Hiperbola dengan sumbu nyata sejajar sumbu X dan titik pusat $ M(0,0) $
2). Persamaan Hiperbola dengan sumbu nyata sejajar sumbu Y dan titik pusat $ M(0,0) $
3). Persamaan Hiperbola dengan sumbu nyata sejajar sumbu X dan titik pusat $ M(p,q) $
4). Persamaan Hiperbola dengan sumbu nyata sejajar sumbu Y dan titik pusat $ M(p,q) $
Pada penjelasan di atas, persamaan Hiperbola jenis (1) sudah kita bahas, tinggal tiga jenis berikutnya.
Persamaan Hiperbola dengan sumbu nyata sejajar sumbu Y dan titik pusat $ M(0,0) $
$ \spadesuit \, $ Persamaan Hiperbola
Pada gambar 3 di atas, persamaan Hiperbolanya adalah
$ - \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 $
$ \clubsuit \, $ Unsur-unsurnya :
-). titik pusat : $ (0,0) $
-). Titik Fokus : $ F_1(0,-c) $ dan $ F_2(0,c) $
-). Titik puncak : titik $A(0,-a)$ dan $B(0,a)$ .
-). Sumbu Utama adalah sumbu Y.
-). Sumbu sekawan adalah sumbu X.
-). Panjang sumbu nyata $ = 2a $
-). Panjang sumbu imajiner $ = 2b $
-). Panjang latus rectum $ = \frac{2b^2}{a} $
-). Eksentrisitas : $ e = \frac{c}{a} $
-). Persamaan direktris : $ y = -\frac{a^2}{c} $ dan $ y = \frac{a^2}{c} $
Pada gambar 3 di atas, persamaan Hiperbolanya adalah
$ - \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 $
$ \clubsuit \, $ Unsur-unsurnya :
-). titik pusat : $ (0,0) $
-). Titik Fokus : $ F_1(0,-c) $ dan $ F_2(0,c) $
-). Titik puncak : titik $A(0,-a)$ dan $B(0,a)$ .
-). Sumbu Utama adalah sumbu Y.
-). Sumbu sekawan adalah sumbu X.
-). Panjang sumbu nyata $ = 2a $
-). Panjang sumbu imajiner $ = 2b $
-). Panjang latus rectum $ = \frac{2b^2}{a} $
-). Eksentrisitas : $ e = \frac{c}{a} $
-). Persamaan direktris : $ y = -\frac{a^2}{c} $ dan $ y = \frac{a^2}{c} $
Persamaan Hiperbola dengan sumbu nyata sejajar sumbu X dan titik pusat $ M(p,q) $
$ \spadesuit \, $ Persamaan Hiperbola
Pada gambar 4 di atas, persamaan Hiperbolanya adalah
$ \frac{(x-p)^2}{a^2} - \frac{(y-q)^2}{b^2} = 1 $
$ \clubsuit \, $ Unsur-unsurnya :
-). titik pusat : $ M(p,q) $
-). Titik puncak : $ F_1(p-c, q) $ dan $ F_2(p+c,q) $
-). Titik puncak : titik $A(p-a,q) \, $ dan $ B(p+a,q)$.
-). Sumbu Utama adalah sumbu X' (garis $ y = q $).
-). Sumbu sekawan adalah sumbu Y' (garis $ x = p $).
-). Panjang sumbu nyata $ = 2a $
-). Panjang sumbu imajiner $ = 2b $
-). Panjang latus rectum $ = \frac{2b^2}{a} $
-). Eksentrisitas : $ e = \frac{c}{a} $
-). Persamaan direktris : $ x = -\frac{a^2}{c} + p $ dan $ x = \frac{a^2}{c} + p $
Pada gambar 4 di atas, persamaan Hiperbolanya adalah
$ \frac{(x-p)^2}{a^2} - \frac{(y-q)^2}{b^2} = 1 $
$ \clubsuit \, $ Unsur-unsurnya :
-). titik pusat : $ M(p,q) $
-). Titik puncak : $ F_1(p-c, q) $ dan $ F_2(p+c,q) $
-). Titik puncak : titik $A(p-a,q) \, $ dan $ B(p+a,q)$.
-). Sumbu Utama adalah sumbu X' (garis $ y = q $).
-). Sumbu sekawan adalah sumbu Y' (garis $ x = p $).
-). Panjang sumbu nyata $ = 2a $
-). Panjang sumbu imajiner $ = 2b $
-). Panjang latus rectum $ = \frac{2b^2}{a} $
-). Eksentrisitas : $ e = \frac{c}{a} $
-). Persamaan direktris : $ x = -\frac{a^2}{c} + p $ dan $ x = \frac{a^2}{c} + p $
Persamaan Hiperbola dengan sumbu nyata sejajar sumbu Y dan titik pusat $ M(p,q) $
$ \spadesuit \, $ Persamaan Hiperbola
Pada gambar 5 di atas, persamaan Hiperbolanya adalah
$ -\frac{(x-p)^2}{b^2} + \frac{(y-q)^2}{a^2} = 1 $
$ \clubsuit \, $ Unsur-unsurnya :
-). titik pusat : $ M(p,q) $
-). Titik puncak : $ F_1(p, q - c) $ dan $ F_2(p, q + c) $
-). Titik puncak : titik $A(p, q - a) \, $ dan $ B(p, q + a)$.
-). Sumbu Utama adalah sumbu Y' (garis $ x = p $).
-). Sumbu sekawan adalah sumbu X' (garis $ y = q $).
-). Panjang sumbu nyata $ = 2a $
-). Panjang sumbu imajiner $ = 2b $
-). Panjang latus rectum $ = \frac{2b^2}{a} $
-). Eksentrisitas : $ e = \frac{c}{a} $
-). Persamaan direktris : $ y = -\frac{a^2}{c} + q $ dan $ y = \frac{a^2}{c} + q $
Pada gambar 5 di atas, persamaan Hiperbolanya adalah
$ -\frac{(x-p)^2}{b^2} + \frac{(y-q)^2}{a^2} = 1 $
$ \clubsuit \, $ Unsur-unsurnya :
-). titik pusat : $ M(p,q) $
-). Titik puncak : $ F_1(p, q - c) $ dan $ F_2(p, q + c) $
-). Titik puncak : titik $A(p, q - a) \, $ dan $ B(p, q + a)$.
-). Sumbu Utama adalah sumbu Y' (garis $ x = p $).
-). Sumbu sekawan adalah sumbu X' (garis $ y = q $).
-). Panjang sumbu nyata $ = 2a $
-). Panjang sumbu imajiner $ = 2b $
-). Panjang latus rectum $ = \frac{2b^2}{a} $
-). Eksentrisitas : $ e = \frac{c}{a} $
-). Persamaan direktris : $ y = -\frac{a^2}{c} + q $ dan $ y = \frac{a^2}{c} + q $
Ada dua hal yang akan menjadi pertanyaan pada soal yaitu pertama : diketahui persamaan Hiperbolanya dan kita diminta menentukan unsur-unsur Hiperbolanya sekaligus gambar grafiknya, dan yang kedua : diketahui unsur-unsur Hiperbolanya dan kita diminta menentukan persamaan Hiperbolanya.
$ \spadesuit \, $ Trik mudah menentukan unsur-unsur pada Hiperbola yang diketahui persamaan Hiperbolanya
Trik (I) : nilai $ a^2 $ adalah nilai yang ada dibawah bagian positif, sehingga sisanya adalah nilai $ b^2 $.
Trik (II) : Letak nilai $ a^2 $ menentukan sumbu nyatanya. Jika $ a $ ada di bawah X, maka sumbu nyatanya sejajar sumbu X dengan persamaan Hiperbolanya $ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $ atau $ \frac{(x-p)^2}{a^2} - \frac{(y-q)^2}{b^2} = 1 $. Jika $ a $ ada di bawah sumbu Y, maka sumbu nyatanya sejajar sumbu Y dengan persamaan Hiperbolanya $ -\frac{x^2}{b^2} +\frac{y^2}{a^2} = 1 $ atau $ -\frac{(x-p)^2}{b^2} + \frac{(y-q)^2}{a^2} = 1 $.
Trik (III) : Nilai $ c $ kita tentukan dari $ c^2 = a^2 + b^2 $.
Triks (IV) : Untuk menentukan titik fokus dan titik puncak, kita tinggal menggeser titik pusat $ M(p,q) $ searah sumbu X atau searah sumbu Y. Jika searah sumbu X maka yang berubah bagian $ x $ saja yaitu kekanan ditambah dan ke kiri dikurangkan. Jika searah sumbu Y maka yang berubah bagian $ y $ saja yaitu ke atas ditambahkan dan ke bawah dikurangkan. Ditambah atau dikurangkan tergantung dari besar pergeserannya yaitu $ a $ atau $ c $. Nilai $ c $ selalu menggeser ke titik fokus, nilai $ a $ menggeser ke titik puncak.
Trik (V) : titik fokus dan titik puncak selalu ada di sumbu nyata.
Contoh Soal Persamaan Hiperbola dan Unsur-unsurnya :
1). Tentukan titik pusat, titik fokus, titik puncak, panjang sumbu nyata, panjang sumbu imajiner, panjang latus rectum, persamaan direktris, dan nilai eksentrisitasnya dari persamaan Hiperbola berikut ini :
a). $ \frac{x^2}{9} - \frac{y^2}{16} = 1 $
b). $ -9x^2 + 4y^2 = 36 $
Penyelesaian :
a). Persamaan Hiperbolanya : $ \frac{x^2}{9} - \frac{y^2}{16} = 1 $
*). Menentukan nilai $ a , b $ dan $ c $ :
-). Karena bagian $ x $ yang positif, maka $ a^2 $ ada di bawah $ x $.
$ a^2 = 9 \rightarrow a = 3 $
$ b^2 = 16 \rightarrow b = 4 $
$ c^2 = a^2 + b^2 \rightarrow c^2 = 9 + 16 \rightarrow c^2 = 25 \rightarrow c = 5 $.
*). Karena $ a $ ada di bawah X, maka sumbu nyatanya sejajar sumbu X, sehingga persamaaan yang dipakai $ \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 $.
*). Menentukan unsur-unsurnya :
-). Panjang sumbu nyata $ = 2a = 2 . 3 = 6 $
-). Panjang sumbu imajiner $ = 2b = 2 . 4 = 8 $
-). Panjang latus rectum $ = \frac{2b^2}{a} = \frac{2.4^2}{3} = \frac{32}{3} $
-). Eksentrisitas : $ e = \frac{c}{a} = \frac{5}{3} $
-). Persamaan direktris :
$ x = -\frac{a^2}{c} = - \frac{9}{5} \, $ atau $ x = \frac{a^2}{c} = \frac{9}{5} $
sehingga persamaan direktrisnya $ x = - \frac{9}{5} $ atau $ x = \frac{9}{5} $
-). Titik pusat : $ M(p,q) = (0,0) $
-). Titik fokus pada sumbu X (sumbu nyata), $ x $ nya berubah dengan $ c = 5 $:
$ F_1(0-5,0) = (-5,0) $
$ F_2(0+5,0) = (5,0) $
-). Titik Puncak pada sumbu X (sumbu nyata), $ x $ nya berubah dengan $ a = 3 $:
$ A(0-3,0) = (-3,0) $
$ B(0+3,0) = (3,0) $
b). Persamaan Hiperbolanya : $ -9x^2 + 4y^2 = 36 $
*). Mengubah persamaannya :
$ \begin{align} -9x^2 + 4y^2 & = 36 \, \, \, \, \, \, \text{(bagi 36)} \\ -\frac{9x^2}{36} + \frac{4y^2}{36} & = \frac{36}{36} \\ -\frac{x^2}{4} + \frac{y^2}{9} & = 1 \end{align} $
*). Menentukan nilai $ a , b $ dan $ c $ :
-). Karena bagian $ y $ yang positif, maka $ a^2 $ ada di bawah $ y $.
$ a^2 = 9 \rightarrow a = 3 $
$ b^2 = 4 \rightarrow b = 2 $
$ c^2 = a^2 + b^2 \rightarrow c^2 = 9 + 4 \rightarrow c^2 = 13 \rightarrow c = \sqrt{13} $.
*). Karena $ a $ ada di bawah Y, maka sumbu nyatanya sejajar sumbu Y, sehingga persamaaan yang dipakai $ -\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 $.
*). Menentukan unsur-unsurnya :
-). Panjang sumbu nyata $ = 2a = 2 . 3 = 6 $
-). Panjang sumbu imajiner $ = 2b = 2 . 2 = 4 $
-). Panjang latus rectum $ = \frac{2b^2}{a} = \frac{2.2^2}{3} = \frac{8}{3} $
-). Eksentrisitas : $ e = \frac{c}{a} = \frac{\sqrt{13}}{3} $
-). Persamaan direktris :
$ x = -\frac{a^2}{c} = - \frac{9}{\sqrt{13}} \, $ atau $ x = \frac{a^2}{c} = \frac{9}{\sqrt{13}} $
sehingga persamaan direktrisnya $ x = - \frac{9}{\sqrt{13}} $ atau $ x = \frac{9}{\sqrt{13}} $
-). Titik pusat : $ M(p,q) = (0,0) $
-). Titik fokus pada sumbu Y (sumbu nyata), $ y $ nya berubah dengan $ c = \sqrt{13} $:
$ F_1(0,0-\sqrt{13}) = (0,-\sqrt{13}) $
$ F_2(0,0+\sqrt{13}) = (0,\sqrt{13}) $
-). Titik Puncak pada sumbu Y (sumbu nyata), $ y $ nya berubah dengan $ a = 3 $:
$ A(0,0-3) = (0,-3) $
$ B(0,0+3) = (0,3) $
2). Tentukan titik pusat, titik fokus, titik puncak, panjang sumbu nyata, panjang sumbu imajiner, panjang latus rectum, persamaan direktris, dan nilai eksentrisitasnya dari persamaan Hiperbola berikut ini :
a). $ \frac{(x+1)^2}{36} - \frac{(y-2)^2}{64} = 1 $
b). $ -\frac{(x-1)^2}{25} + \frac{(y-3)^2}{144} = 1 $
Penyelesaian :
a). Persamaan Hiperbolanya : $ frac{(x+1)^2}{36} - \frac{(y-2)^2}{64} = 1 $
*). Menentukan nilai $ a , b , c , p $ dan $ q $ :
-). Karena bagian $ x $ yang positif, maka $ a^2 $ ada di bawah $ x $.
$ a^2 = 36 \rightarrow a = 6 $
$ b^2 = 64 \rightarrow b = 8 $
$ c^2 = a^2 + b^2 \rightarrow c^2 = 36 + 64 \rightarrow c^2 = 100 \rightarrow c = 10 $.
$ x - p = x + 1 \rightarrow p = -1 $
$ y - q = y - 2 \rightarrow q = 2 $
*). Karena $ a $ ada di bawah X, maka sumbu nyatanya sejajar sumbu X, sehingga persamaaan yang dipakai $ \frac{(x-p)^2}{a^2} - \frac{(y-b)^2}{b^2} = 1 $.
*). Menentukan unsur-unsurnya :
-). Panjang sumbu nyata $ = 2a = 2 . 6 = 12 $
-). Panjang sumbu imajiner $ = 2b = 2 . 8 = 16 $
-). Panjang latus rectum $ = \frac{2b^2}{a} = \frac{2.8^2}{6} = \frac{64}{6} = \frac{32}{3} $
-). Eksentrisitas : $ e = \frac{c}{a} = \frac{10}{6} = \frac{5}{3} $
-). Persamaan direktris :
$ x = -\frac{a^2}{c} + p = - \frac{6^2}{10} + (-1) = - \frac{23}{5} \, $
atau $ x = \frac{a^2}{c} + p = \frac{6^2}{10} + (-1) = \frac{8}{5} $
sehingga persamaan direktrisnya $ x = - \frac{23}{5} $ atau $ x = \frac{8}{5} $
-). Titik pusat : $ M(p,q) = (-1,2) $
-). Titik fokus sejajar sumbu X (sumbu nyata), $ x $ nya berubah dengan $ c = 10 $:
$ F_1(-1-10,2) = (-11,2) $
$ F_2(-1+10,2) = (9,2) $
-). Titik Puncak sejajar sumbu X (sumbu nyata), $ x $ nya berubah dengan $ a = 6 $:
$ A(-1-6,2) = (-7,2) $
$ B(-1+6,2) = (5,2) $
b). Persamaan Hiperbolanya : $ -\frac{(x-1)^2}{25} + \frac{(y-3)^2}{144} = 1 $
*). Menentukan nilai $ a , b , c , p $ dan $ q $ :
-). Karena bagian $ y $ yang positif, maka $ a^2 $ ada di bawah $ y $.
$ a^2 = 144 \rightarrow a = 12 $
$ b^2 = 25 \rightarrow b = 5 $
$ c^2 = a^2 + b^2 \rightarrow c^2 = 144 + 25 \rightarrow c^2 = 169 \rightarrow c = 13 $.
$ x-p = x - 1 \rightarrow p = 1 $
$ y - q = y - 3 \rightarrow q = 3 $
*). Karena $ a $ ada di bawah Y, maka sumbu nyatanya sejajar sumbu Y, sehingga persamaaan yang dipakai $ -\frac{(x-p)^2}{b^2} + \frac{(y-q)^2}{a^2} = 1 $.
*). Menentukan unsur-unsurnya :
-). Panjang sumbu nyata $ = 2a = 2 . 12 = 24 $
-). Panjang sumbu imajiner $ = 2b = 2 . 5 = 10 $
-). Panjang latus rectum $ = \frac{2b^2}{a} = \frac{2.5^2}{12} = \frac{25}{6} $
-). Eksentrisitas : $ e = \frac{c}{a} = \frac{13}{12} $
-). Persamaan direktris :
$ y = -\frac{a^2}{c} + q = - \frac{12^2}{13} + 3 = -\frac{105}{13} \, $
atau $ y = \frac{a^2}{c} + q = \frac{12^2}{13} + 3 = \frac{183}{13} $
sehingga persamaan direktrisnya $ x = -\frac{105}{13} $ atau $ x = \frac{183}{13} $
-). Titik pusat : $ M(p,q) = (1,3) $
-). Titik fokus sejajar sumbu Y (sumbu nyata), $ y $ nya berubah dengan $ c = 13 $:
$ F_1(1, 3 - 13) = (1,-10) $
$ F_2(1,3+13) = (1,16) $
-). Titik Puncak sejajar sumbu Y (sumbu nyata), $ y $ nya berubah dengan $ a = 12 $:
$ A(1,3-12) = (1,-9) $
$ B(1,3+12) = (1,15) $
3). Tentukan titik pusat, titik fokus, titik puncak, panjang sumbu nyata, panjang sumbu imajiner, panjang latus rectum, persamaan direktris, dan nilai eksentrisitasnya dari persamaan Hiperbola $ 9x^2 - 16y^2 + 36x - 32y - 122 = 0 $ !
Penyelesaian :
*). Kita ubah persamaan Hiperbolanya dengan "cara melengkapkan kuadrat sempurna"
$ \begin{align} 9x^2 - 16y^2 + 36x - 32y - 122 & = 0 \\ 9x^2 + 36x - 16y^2 - 32y & = 122 \\ 9(x^2 + 4x) - 16(y^2 + 2y) & = 122 \\ 9[(x + \frac{4}{2})^2 - (\frac{4}{2})^2] - 16[(y + \frac{2}{2})^2 - (\frac{2}{2})^2 ] & = 122 \\ 9[(x +2)^2 - 4] - 16[(y + 1)^2 - 1 ] & = 122 \\ 9(x +2)^2 - 36 - 16(y - 1)^2 + 16 & = 122 \\ 9(x +2)^2 - 16(y - 1)^2 & = 122 + 36 - 16 \\ 9(x +2)^2 - 16(y - 1)^2 & = 144 \, \, \, \, \, \text{(bagi 144)} \\ \frac{9(x +2)^2}{144} - \frac{16(y - 1)^2}{144} & = \frac{144}{144} \\ \frac{(x +2)^2}{16} - \frac{(y - 1)^2}{9} & = 1 \end{align} $
*). Langkah berikutnya mirip dengan contoh (2) di atas bagian (a).
$ \clubsuit \, $ Trik mudah menentukan persamaan Hiperbola yang diketahui unsur-unsurnya
Berikut ada beberapa trik mudah sehingga kita tidak perlu mengingat semua rumus persamaan Hiperbolanya jika diketahui unsur-unsur Hiperbolanya.
i). Diketahui titik fokus, perhatikan bagian $ x $ atau $ y $ kah yang berubah. Jika yang berubah $ x $ nya, maka sumbu nyata sejajar sumbu X dengan persamaan Hiperbola $ \frac{(x-p)^2}{a^2} - \frac{(y-q)^2}{b^2} = 1 $. Jika yang berubah $ y $ nya, maka sumbu nyata sejajar sumbu Y dengan persamaan Hiperbola $ - \frac{(x-p)^2}{b^2} + \frac{(y-q)^2}{a^2} = 1 $.
ii). Jarak duat titik fokus dan puncak :
Jarak dua titik fokus $ = 2c $
Jarak dua titik puncak = $ 2a $
iii). gunakan juga teorema pythagoras : $ c^2 = a^2 + b^2 $
iv). Untuk menentukan titik pusat $ M(p,q) $ , kita menggunakan konsep titik tengah antara dua titik. Titik tengah antara titik $ (x_1,y_1) $ dan titik $ (x_2,y_2) $ adalah $ \left( \frac{x_1+x_2}{2}, \frac{y_1+y_2}{2} \right) $ . Titik pusat selalu ditengah-tengah antara dua titik fokus dan juga ditengah-tengah antara dua titik puncak.
Contoh soal diketahui unsur-unsur Hiperbola :
4). Tentukan persamaan Hiperbola jika diketahui :
a). Titik fokus (2,3) dan (6,3) serta panjang sumbu nyata 2.
b). Titik fokus $(-1,-3) $ dan $ (-1,5) $ serta panjang sumbu imajiner 4.
Penyelesaian :
a). Titik fokus (2,3) dan (6,3), yang berubah $ x $ nya, sehingga sumbu nyatanya sejajar sumbu X dengan persamaan Hiperbola $ \frac{(x-p)^2}{a^2} - \frac{(y-q)^2}{b^2} = 1 $.
*). Titik pusat diantara dua titik fokus :
$ (p,q) = \left( \frac{2 + 6}{2}, \frac{3+3}{2} \right) = (4,3) $
*). Menentukan nilai $ a $ dan $ b $ :
-). Panjang sumbu nyata = 2 ,
$ 2a = 2 \rightarrow a = 1 $
-). Jarak dua fokus = $ 6-2 = 4 $
$ 2 c = 4 \rightarrow c = 2 $
-). $ c^2 = a^2 + b^2 \rightarrow 4 = b^2 + 1 \rightarrow b^2 = 3 $.
*). Menentukan persamaan Hiperbolanya :
$ \begin{align} \frac{(x-p)^2}{a^2} - \frac{(y-q)^2}{b^2} & = 1 \\ \frac{(x-4)^2}{1} - \frac{(y-3)^2}{3} & = 1 \end{align} $
Jadi, persamaan Hiperbolanya $ \frac{(x-4)^2}{1} - \frac{(y-3)^2}{3} = 1 $.
b). Titik fokus $(-1,-3) $ dan $ (-1,5) $, yang berubah $ y $ nya, sehingga sumbu nyatanya sejajar sumbu Y dengan persamaan Hiperbola $ -\frac{(x-p)^2}{b^2} + \frac{(y-q)^2}{a^2} = 1 $.
*). Titik pusat diantara dua titik fokus :
$ (p,q) = \left( \frac{-1 + (-1)}{2}, \frac{-3 + 5}{2} \right) = (-1,1) $
*). Menentukan nilai $ a $ dan $ b $ :
-). Panjang sumbu imajiner = 4 ,
$ 2b = 4 \rightarrow b = 2 $
-). Jarak dua fokus = $ 5 - (-3) = 8 $
$ 2 c = 8 \rightarrow c = 4 $
-). $ c^2 = a^2 + b^2 \rightarrow 16 = a^2 + 4 \rightarrow a^2 = 12 $.
*). Menentukan persamaan Hiperbolanya :
$ \begin{align} -\frac{(x-p)^2}{b^2} + \frac{(y-q)^2}{a^2} & = 1 \\ -\frac{(x-(-1))^2}{4} + \frac{(y-1)^2}{12} & = 1 \\ -\frac{(x+1)^2}{4} + \frac{(y-1)^2}{12} & = 1 \end{align} $
Jadi, persamaan Hiperbolanya $ -\frac{(x+1)^2}{4} + \frac{(y-1)^2}{12} = 1 $.
5). Tentukan persamaan Hiperbola yang diketahui titik fokusnya $ (-4,1) $ dan $ (6,1) $ serta titik puncaknya $ (-2,1) $ dan $ (4,1) $!
Penyelesaian :
*). Titik fokus $ (-4,1) $ dan $ (6,1) $, yang berubah $ x $ nya, sehingga sumbu nyatanya sejajar sumbu X dengan persamaan Hiperbola $ \frac{(x-p)^2}{a^2} - \frac{(y-q)^2}{b^2} = 1 $.
*). Titik pusat diantara dua titik fokus :
$ (p,q) = \left( \frac{-4 + 6}{2}, \frac{1 + 1}{2} \right) = (1,1) $
*). Menentukan nilai $ a $ dan $ b $ :
-). Jarak dua fokus = $ 6 - (-4) = 10 $
$ 2 c = 10 \rightarrow c = 5 $
-). Titik puncak $ (-2,1) $ dan $ (4,1) $.
Jarak dua titik puncak = $ 4 - (-2) = 6 $
$ 2 a = 6 \rightarrow a = 3 $
-). $ c^2 = a^2 + b^2 \rightarrow 25 = 9 + b^2 \rightarrow b^2 = 16 $.
*). Menentukan persamaan Hiperbolanya :
$ \begin{align} \frac{(x-p)^2}{a^2} - \frac{(y-q)^2}{b^2} & = 1 \\ \frac{(x-1)^2}{9} - \frac{(y-1)^2}{16} & = 1 \end{align} $
Jadi, persamaan Hiperbolanya $ \frac{(x-1)^2}{9} - \frac{(y-1)^2}{16} = 1 $.
6). Tentukan persamaan Hiperbola yang diketahui titik fokusnya $ (1,1) $ dan $ (1,5) $ serta titik puncaknya $ (1,2) $ dan $ (1,4) $!
Penyelesaian :
*). Titik fokus $ (1,1) $ dan $ (1,5) $, yang berubah $ y $ nya, sehingga sumbu nyatanya sejajar sumbu Y dengan persamaan Hiperbola $ -\frac{(x-p)^2}{b^2} + \frac{(y-q)^2}{a^2} = 1 $.
*). Titik pusat diantara dua titik fokus :
$ (p,q) = \left( \frac{1+1}{2}, \frac{1 + 5}{2} \right) = (1,3) $
*). Menentukan nilai $ a $ dan $ b $ :
-). Jarak dua fokus = $ 5 - 1 = 4 $
$ 2 c = 4 \rightarrow c = 2 $
-). Titik puncak $ (1,2) $ dan $ (1,4) $.
Jarak dua titik puncak = $ 4 - 2 = 2 $
$ 2a = 2 \rightarrow a = 1 $
-). $ c^2 = a^2 + b^2 \rightarrow 4 = 1 + b^2 \rightarrow b^2 = 3 $.
*). Menentukan persamaan Hiperbolanya :
$ \begin{align} -\frac{(x-p)^2}{b^2} + \frac{(y-q)^2}{a^2} & = 1 \\ -\frac{(x-1)^2}{3} + \frac{(y-3)^2}{1} & = 1 \end{align} $
Jadi, persamaan Hiperbolanya $ -\frac{(x-1)^2}{3} + \frac{(y-3)^2}{1} = 1 $.
7). Tentukan persamaan Hiperbola jika diketahui titik fokus $ (1,2) $ dan $ (1,6) $ serta nilai eksentrisitasnya $ 2 $ !
Penyelesaian :
*). Titik fokus $ (1,2) $ dan $ (1,6) $, yang berubah $ y $ nya, sehingga sumbu nyatanya sejajar sumbu Y dengan persamaan Hiperbola $ -\frac{(x-p)^2}{b^2} + \frac{(y-q)^2}{a^2} = 1 $.
*). Titik pusat diantara dua titik fokus :
$ (p,q) = \left( \frac{1+1}{2}, \frac{2 + 6}{2} \right) = (1,4) $
*). Menentukan nilai $ a $ dan $ b $ :
-). Jarak dua fokus = $ 6 - 2 = 4 $
$ 2 c = 4 \rightarrow c = 2 $
-). Eksentrisitas :
$ e = 2 \rightarrow \frac{c}{a} = 2 \rightarrow \frac{2}{a} = 2 \rightarrow a = 1 $
-). $ c^2 = a^2 + b^2 \rightarrow 4 = 1 + b^2 \rightarrow b^2 = 3 $.
*). Menentukan persamaan Hiperbolanya :
$ \begin{align} -\frac{(x-p)^2}{b^2} + \frac{(y-q)^2}{a^2} & = 1 \\ -\frac{(x-1)^2}{3} + \frac{(y-4)^2}{1} & = 1 \end{align} $
Jadi, persamaan Hiperbolanya $ -\frac{(x-1)^2}{3} + (y-4)^2 = 1 $.
8). Tentukan persamaan Hiperbola jika diketahui titik puncak $ (-4,3) $ dan $ (2,3) $ serta salah satu persamaan direktrisnya adalah $ x = -\frac{14}{5} $ !
Penyelesaian :
*). Titik puncak $ (-4,3) $ dan $ (2,3) $, yang berubah $ x $ nya, sehingga sumbu nyatanya sejajar sumbu X dengan persamaan Hiperbola $ \frac{(x-p)^2}{a^2} - \frac{(y-q)^2}{b^2} = 1 $.
*). Titik pusat diantara dua titik Puncak :
$ (p,q) = \left( \frac{-4+2}{2}, \frac{3 + 3}{2} \right) = (-1,3) $
*). Menentukan nilai $ a $ dan $ b $ :
-). Jarak dua puncak = $ 2- (-4) = 6 $
$ 2 a = 6 \rightarrow a = 3 $
-). Persamaan direktrisnya $ x = -\frac{14}{5} $ ada di sebelah kiri titik puncak, sehingga persamaan direktrisnya $ x = -\frac{a^2}{c} + p $ :
$ -\frac{a^2}{c} + p = -\frac{14}{5} \rightarrow -\frac{3^2}{c} + (-1) = -\frac{9}{5} -1 \rightarrow -\frac{9}{c} = -\frac{9}{5} \rightarrow c = 5 $
-). $ c^2 = a^2 + b^2 \rightarrow 25 = 9 + b^2 \rightarrow b^2 = 16 $.
*). Menentukan persamaan Hiperbolanya :
$ \begin{align} \frac{(x-p)^2}{a^2} - \frac{(y-q)^2}{b^2} & = 1 \\ \frac{(x-(-1))^2}{9} - \frac{(y-3)^2}{16} & = 1 \\ \frac{(x+1)^2}{9} - \frac{(y-3)^2}{16} & = 1 \end{align} $
Jadi, persamaan Hiperbolanya $ \frac{(x+1)^2}{9} - \frac{(y-3)^2}{16} = 1 $.
Demikian pembahasan materi Persamaan Hiperbola dan Unsur-unsurnya serta contoh-contohnya. Silahkan juga baca materi lain yang berkaitan dengan "irisan kerucut" yaitu "kedudukan titik dan garis terhadap Hiperbola".