Untuk memudahkan mempelajari materi Kedudukan Titik terhadap Elips, kita harus menguasai beberapa materi inti seperti "persamaan elips", dan "penyelesaian pertidaksamaan". Untuk lebih lengkapnya, mari kita bahas syarat apa saja untuk mengetahui jenis masing-masing kedudukan titik terhadap elips berikut ini.
Syarat Kedudukan Titik terhadap Elips
Untuk mengetahui Kedudukan Titik terhadap Elips, kita
substitusi titik tersebut ke persamaan elipsnya sehingga akan kita peroleh tiga kemungkinan yaitu :
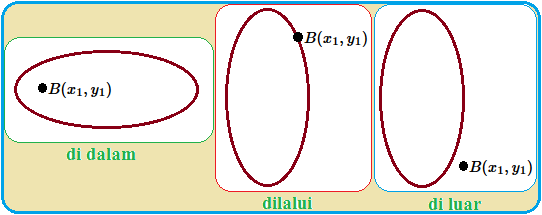
1). Jika nilai ruas kiri $ < $ ruas kanan (lebih kecil), maka titik ada di dalam elips,
2). Jika nilai ruas kiri $ = $ ruas kanan, maka titik ada pada elips (titik dilalui oleh elips),
3). Jika nilai ruas kiri $ > $ ruas kanan (lebih besar), maka titik ada di luar elips.
1). Jika nilai ruas kiri $ < $ ruas kanan (lebih kecil), maka titik ada di dalam elips,
2). Jika nilai ruas kiri $ = $ ruas kanan, maka titik ada pada elips (titik dilalui oleh elips),
3). Jika nilai ruas kiri $ > $ ruas kanan (lebih besar), maka titik ada di luar elips.
Bentuk persamaan elipsnya harus memenuhi bentuk umumnya, setelah itu baru bisa kita substitusi titik yang mau kita cek kedudukannya terhadap elips tersebut. Bentuk yang dimaksud adalah $ \frac{(x-p)^2}{a^2}+ \frac{(y-q)^2}{b^2} = 1 $ atau $ \frac{(x-p)^2}{b^2}+ \frac{(y-q)^2}{a^2} = 1 $ atau $ Ax^2 + By^2 + Cx + Dy + E = 0 $.
Contoh Soal Kedudukan Titik terhadap Elips :
1). Tentukan kedudukan titik $ (1,-1) $ terhadap elips $ \frac{x^2}{9} + \frac{y^2}{4} = 1 $!
Penyelesaian :
*). Substitusi titik $ (1,-1) $ ke persamaan elips :
$ \begin{align} (x,y)=(1,-1) \rightarrow \frac{x^2}{9} + \frac{y^2}{4} & = 1 \\ \frac{1^2}{9} + \frac{(-1)^2}{4} & ... 1 \\ \frac{1}{9} + \frac{1}{4} & ... 1 \\ \frac{13}{36} & ... 1 \\ \frac{13}{36} & < 1 \end{align} $
Karena ruas kiri $ < $ ruas kanan ( $ \frac{13}{36} < 1 $) , maka titik $ (1,-1) $ ada di dalam elips. Berikut ilustrasi gambarnya,
2). Tentukan kedudukan titik $ (6,-3) $ terhadap elips $ \frac{(x-1)^2}{25} + \frac{(y+3)^2}{100} = 1 $!
Penyelesaian :
*). Substitusi titik $ (6,-3) $ ke persamaan elips :
$ \begin{align} (x,y)=(6,-3) \rightarrow \frac{(x-1)^2}{25} + \frac{(y+3)^2}{100} & = 1 \\ \frac{(6-1)^2}{25} + \frac{(-3+3)^2}{100} & ... 1 \\ \frac{25}{25} + \frac{0}{100} & ... 1 \\ 1 + 0 & ... 1 \\ 1 & ... 1 \\ 1 & = 1 \end{align} $
Karena ruas kiri $ = $ ruas kanan ( $ 1 = 1 $) , maka titik $ (6,-3) $ ada pada elips (titik tersebut dilalui oleh kurva elips). Berikut ilustrasi gambarnya,
3). Tentukan kedudukan titik $ (-2,1) $ terhadap elips $ 9x^2 + 4y^2 + 16y - 20 = 0 $!
Penyelesaian :
*). Substitusi titik $ (-2,1) $ ke persamaan elips :
$ \begin{align} (x,y)=(-2,1) \rightarrow 9x^2 + 4y^2 + 16y - 20 & = 0 \\ 9(-2)^2 + 4.1^2 + 16.1 - 20 & ... 0 \\ 36 + 4 + 16 - 20 & ... 0 \\ 36 & ... 0 \\ 36 & > 0 \end{align} $
Karena ruas kiri $ > $ ruas kanan ( $ 36 > 0 $) , maka titik $ (-2,1) $ ada di luar elips. Berikut ilustrasi gambarnya,
4). Jika titik $ (3,-1) $ ada pada elips (dilalui elips) $ \frac{(x-k)^2}{4} + \frac{(y+1)^2}{9} = 1 $ , maka tentukan nilai $ k_1 + k_2 $!
Penyelesaian :
*). Substitusi titik $(3,-1) $ ke persamaan elipsnya :
$ \begin{align} (x,y) & = (3,-1) \\ \frac{(x-k)^2}{4} + \frac{(y+1)^2}{9} & = 1 \\ \frac{(3-k)^2}{4} + \frac{(-1+1)^2}{9} & = 1 \\ \frac{(3-k)^2}{4} + \frac{0}{9} & = 1 \\ \frac{(3-k)^2}{4} & = 1 \\ (3-k)^2 & = 4 \\ 3-k & = \pm \sqrt{4} = \pm 2 \\ 3-k = 2 \vee 3 - k & = -2 \\ k_1 = 1 \vee k_2 & = 5 \\ \end{align} $
*). Sehingga nilai :
$ k_1 + k_2 = 1 + 5 = 6 $
Jadi, nilai $ k_1 + k_2 = 6 $.
5). Jika titik $ (1,2) $ ada di luar elips $ 2x^2 + py^2 + 3x- 4y + 7 = 0 $ , maka tentukan nilai $ p $ yang memenuhi!
Penyelesaian :
*). Substitusi titik $ (1,2) $ dan syarat ada di luar adalah $ > $ :
$ \begin{align} (x,y) & = (1,2) \\ 2x^2 + py^2 + 3x- 4y + 7 & = 0 \\ 2.1^2 + p.2^2 + 3.1- 4.1 + 7 & > 0 \\ 2 + 4p + 3 - 4 + 7 & > 0 \\ 4p + 8 & > 0 \\ 4p & > - 8 \\ p & > -2 \end{align} $
Jadi, nilai $ p $ yang memenuhi adalah $ p > -2 $.
6). Titik $ (1,k) $ ada di dalam elips $ \frac{(x-1)^2}{4} + \frac{(y+2)^2}{9} = 1 $. Jika $ M $ menyatakan nilai maksimum dari $ k $ dan $ N $ menyatakan nilai minimum dari $ k $ , maka tentukan nilai $ M - N $ dengan $ M $ dan $ N $ adalah bilangan bulat!
Penyelesaian :
*). Substitusi titik $ (1,k) $ dan syarat ada di dalam adalah $ < $ :
$ \begin{align} (x,y) & = (1,k) \\ \frac{(x-1)^2}{4} + \frac{(y+2)^2}{9} & = 1 \\ \frac{(1-1)^2}{4} + \frac{(k+2)^2}{9} & < 1 \\ \frac{0}{4} + \frac{k^2 + 4k + 4}{9} & < 1 \\ \frac{k^2 + 4k + 4}{9} & < 1 \\ k^2 + 4k + 4 & < 9 \\ k^2 + 4k -5 & < 0 \\ (k +5)(k-1) & < 0 \\ k = -5 \vee k & = 1 \end{align} $
Garis bilangannya :
Solusinya : $ \{ -5 < k < 1 \} $.
Artinya nilai $ M = 0 $ dan $ N = -4 $.
Sehingga nilai $ M - N = 0 - (-4) = 4 $.
Jadi, nilai $ M - N = 4 $.
Demikian pembahasan materi Kedudukan Titik terhadap Elips dan contoh-contohnya. Silahkan juga baca materi lain yang berkaitan dengan "irisan kerucut" yaitu "Kedudukan Garis terhadap Elips".