Untuk memudahkan mempelajari artikel Komposisi Rotasi Sepusat ini, teman-teman harus menguasai materi "Rotasi pada Transformasi Geometri", "Matriks Transformasi Geometri", dan operasi pada matriks. Untuk Pengerjaannya juga seperti biasa yaitu $ bayangan \, = \, matriks \times awal $. Langsung saja kita simak penjelasannya berikut ini.
Pengerjaan Komposisi Rotasi Sepusat
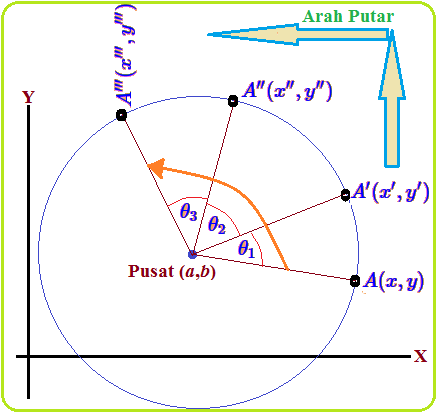
Perhatikan ilustrasi gambar komposisi rotasi sepusat di atas, pusat rotasi adalah $(a,b)$ dengan titik awal
$A(x,y)$ dilakukan rotasi sebesar $ \theta _1 $ menghasilkan bayangan $A^\prime (x^\prime , y^\prime )$, dilanjutkan lagi rotasi
sebesar $ \theta _2 $ menghasilkan bayangan $ A^{\prime \prime } (x^{\prime \prime } , y^{\prime \prime } ) $, dan dilanjutkan lagi rotasi sebesar
$ \theta _3 $ menghasilkan bayangan $ A^{\prime \prime \prime } (x^{\prime \prime \prime } , y^{\prime \prime \prime } ) $ .
*). Matriks gabungannya :
$ MT = \left( \begin{matrix} \cos (\theta _1 + \theta _2 + \theta _3 ) & - \sin (\theta _1 + \theta _2 + \theta _3 ) \\ \sin (\theta _1 + \theta _2 + \theta _3 ) & \cos (\theta _1 + \theta _2 + \theta _3 ) \end{matrix} \right) $
Catatan :
Nilai $ \theta _1 , \, \theta _2 , \, $ dan $ \theta _3 $ bisa bernilai negatif tergantung dari arah putaran terhadap jarum jam.
Jika searah jarum jam, maka sudutnya negatif.
Jika berlawanan arah jarum jam, maka sudutnya positif.
*). titik pusat (0,0)
$ \left( \begin{matrix} x^\prime \\ y^\prime \end{matrix} \right) = (MT) \times \left( \begin{matrix} x \\ y \end{matrix} \right) $
*). titik pusat $(a,b)$
$ \left( \begin{matrix} x^\prime \\ y^\prime \end{matrix} \right) = ( MT) \times \left( \begin{matrix} x - a \\ y - b \end{matrix} \right) + \left( \begin{matrix} a \\ b \end{matrix} \right) $
*). Matriks gabungannya :
$ MT = \left( \begin{matrix} \cos (\theta _1 + \theta _2 + \theta _3 ) & - \sin (\theta _1 + \theta _2 + \theta _3 ) \\ \sin (\theta _1 + \theta _2 + \theta _3 ) & \cos (\theta _1 + \theta _2 + \theta _3 ) \end{matrix} \right) $
Catatan :
Nilai $ \theta _1 , \, \theta _2 , \, $ dan $ \theta _3 $ bisa bernilai negatif tergantung dari arah putaran terhadap jarum jam.
Jika searah jarum jam, maka sudutnya negatif.
Jika berlawanan arah jarum jam, maka sudutnya positif.
*). titik pusat (0,0)
$ \left( \begin{matrix} x^\prime \\ y^\prime \end{matrix} \right) = (MT) \times \left( \begin{matrix} x \\ y \end{matrix} \right) $
*). titik pusat $(a,b)$
$ \left( \begin{matrix} x^\prime \\ y^\prime \end{matrix} \right) = ( MT) \times \left( \begin{matrix} x - a \\ y - b \end{matrix} \right) + \left( \begin{matrix} a \\ b \end{matrix} \right) $
Contoh Soal Komposisi Rotasi Sepusat :
1). Titik A(1,2) dirotasi sebesar $35^\circ $ berlawanan arah jarum jam, kemudian dilanjutkan lagi dengan rotasi sebesar $ 55^\circ $ berlawanan arah jarum jam. Jika titik pusat kedua rotasi sama yaitu $ (-3,5) $ , maka tentukan bayangan titik A?
Penyelesaian :
*). Matriks gabungannya :
$ \theta _1 = 35^\circ , \, \theta _2 = 55^\circ \, $ dan titik pusat $(a,b) = (-3,5) $.
$\begin{align} MT & = \left( \begin{matrix} \cos (\theta _1 + \theta _2 ) & - \sin (\theta _1 + \theta _2 ) \\ \sin (\theta _1 + \theta _2 ) & \cos (\theta _1 + \theta _2 ) \end{matrix} \right) \\ & = \left( \begin{matrix} \cos (35^\circ + 55^\circ ) & - \sin (35^\circ + 55^\circ ) \\ \sin (35^\circ + 55^\circ ) & \cos (35^\circ + 55^\circ ) \end{matrix} \right) \\ & = \left( \begin{matrix} \cos (90^\circ ) & - \sin (90^\circ ) \\ \sin (90^\circ ) & \cos (90^\circ ) \end{matrix} \right) = \left( \begin{matrix} 0 & - 1 \\ 1 & 0 \end{matrix} \right) \end{align} $
*). Menentukan bayangan titik A(1,2) :
$ \begin{align} \left( \begin{matrix} x^\prime \\ y^\prime \end{matrix} \right) & = ( MT) \times \left( \begin{matrix} x - a \\ y - b \end{matrix} \right) + \left( \begin{matrix} a \\ b \end{matrix} \right) \\ & = \left( \begin{matrix} 0 & - 1 \\ 1 & 0 \end{matrix} \right) \times \left( \begin{matrix} 1 - (-3) \\ 2 - 5 \end{matrix} \right) + \left( \begin{matrix} -3 \\ 5 \end{matrix} \right) \\ & = \left( \begin{matrix} 0 & - 1 \\ 1 & 0 \end{matrix} \right) \times \left( \begin{matrix} 4 \\ -3 \end{matrix} \right) + \left( \begin{matrix} -3 \\ 5 \end{matrix} \right) \\ & = \left( \begin{matrix} 3 \\ 4 \end{matrix} \right) + \left( \begin{matrix} -3 \\ 5 \end{matrix} \right) \\ & = \left( \begin{matrix} 0 \\ 9 \end{matrix} \right) \end{align} $
Jadi, bayangan titik A adalah $ A^\prime (0,9) . \, \heartsuit $.
2). Persamaan $ y = 3x^4 - 2x - 1 $ dirotasi sebesar $50^\circ $ berlawanan arah jarum jam, kemudian dilanjutkan lagi dengan rotasi sebesar $ 300^\circ $ searah jarum jam, dan dilanjutkan lagi rotasi sebesar $70^\circ $ berlawanan arah jarum jam. Jika titik pusat ketiga rotasi sama yaitu $ (0,0) $ , maka tentukan bayangan persamaan kurva tersebut?
Penyelesaian :
*). Matriks gabungannya :
$ \theta _1 = 50^\circ , \, \theta _2 = -300^\circ, \, \theta _3 = 70^\circ \, $ dan titik pusat $(a,b) = (0,0) $.
$\begin{align} MT & = \left( \begin{matrix} \cos (\theta _1 + \theta _2 + \theta _3 ) & - \sin (\theta _1 + \theta _2 + \theta _3 ) \\ \sin (\theta _1 + \theta _2 + \theta _3 ) & \cos (\theta _1 + \theta _2 + \theta _3 ) \end{matrix} \right) \\ & = \left( \begin{matrix} \cos (50^\circ + (-300^\circ) + 70^\circ ) & - \sin (50^\circ + (-300^\circ) + 70^\circ ) \\ \sin (50^\circ + (-300^\circ) + 70^\circ ) & \cos (50^\circ + (-300^\circ) + 70^\circ ) \end{matrix} \right) \\ & = \left( \begin{matrix} \cos (-180^\circ ) & - \sin (-180^\circ ) \\ \sin (-180^\circ ) & \cos (-180^\circ ) \end{matrix} \right) \\ & = \left( \begin{matrix} \cos (180^\circ ) & \sin (180^\circ ) \\ - \sin (180^\circ ) & \cos (180^\circ ) \end{matrix} \right) = \left( \begin{matrix} -1 & 0 \\ 0 & -1 \end{matrix} \right) \end{align} $
*). Menentukan hubungan $ (x,y) $ dan $ (x^\prime , y^\prime ) $ :
$ \begin{align} \left( \begin{matrix} x^\prime \\ y^\prime \end{matrix} \right) & = ( MT) \times \left( \begin{matrix} x \\ y \end{matrix} \right) \\ \left( \begin{matrix} x^\prime \\ y^\prime \end{matrix} \right) & = \left( \begin{matrix} -1 & 0 \\ 0 & -1 \end{matrix} \right) \times \left( \begin{matrix} x \\ y \end{matrix} \right) \\ \left( \begin{matrix} x^\prime \\ y^\prime \end{matrix} \right) & = \left( \begin{matrix} -x \\ -y \end{matrix} \right) \end{align} $
Kita peroleh :
$ x^\prime = -x \rightarrow x = -x^\prime $ dan $ y^\prime = -y \rightarrow y = -y^\prime $ .
*). Substitusi bentuk $ x = -x^\prime $ dan $ y = -y^\prime $ ke persamaan awal sehingga kita peroleh persamaan bayangannya :
$ \begin{align} y & = 3x^4 - 2x - 1 \\ -y^\prime & = 3(-x^\prime)^4 - 2.(-x^\prime) - 1 \\ -y^\prime & = 3(x^\prime)^4 + 2x^\prime - 1 \\ y^\prime & = - 3(x^\prime)^4 - 2x^\prime + 1 \end{align} $
Sehingga bayangannya $ y^\prime = - 3(x^\prime)^4 - 2x^\prime + 1 $ atau $ y = -3x^4 - 2x + 1 $.
Jadi, persamaan bayangannya adalah $ y = -3x^4 - 2x + 1 . \, \heartsuit $.
3). Titik B($-2,1$) dirotasi sejauh $ 60^\circ $ dengan titik pusat (1,0) , lalu dilanjutkan lagi dengan rotasi sebesar $ 30^\circ $ dengan titik pusat $ (-1,3) $. Tentukan bayangan titik B?
Penyelesaian :
*). Karena titik pusat rotasinya tidak sama, maka matriks rotasinya tidak bisa kita gabung langsung, artinya kita harus mengerjakan satu demi satu bentuk rotasinya.
*). Rotasi pertama : $ \theta _ 1 = 60^\circ $ dengan pusat $(a,b) = (1,0) $.
$ MT = \left( \begin{matrix} \cos (60^\circ ) & - \sin (60^\circ ) \\ \sin (60^\circ ) & \cos (60^\circ ) \end{matrix} \right) = \left( \begin{matrix} \frac{1}{2} & - \frac{1}{2}\sqrt{3} \\ \frac{1}{2}\sqrt{3} & \frac{1}{2} ) \end{matrix} \right) $
Bayangan pertama titik $B(-2,1) $ :
$ \begin{align} \left( \begin{matrix} x^\prime \\ y^\prime \end{matrix} \right) & = ( MT) \times \left( \begin{matrix} x - a \\ y - b \end{matrix} \right) + \left( \begin{matrix} a \\ b \end{matrix} \right) \\ & = \left( \begin{matrix} \frac{1}{2} & - \frac{1}{2}\sqrt{3} \\ \frac{1}{2}\sqrt{3} & \frac{1}{2} ) \end{matrix} \right) \times \left( \begin{matrix} -2 - 1 \\ 1 - 0 \end{matrix} \right) + \left( \begin{matrix} 1 \\ 0 \end{matrix} \right) \\ & = \left( \begin{matrix} \frac{1}{2} & - \frac{1}{2}\sqrt{3} \\ \frac{1}{2}\sqrt{3} & \frac{1}{2} ) \end{matrix} \right) \times \left( \begin{matrix} -3 \\ 1 \end{matrix} \right) + \left( \begin{matrix} 1 \\ 0 \end{matrix} \right) \\ & = \left( \begin{matrix} \frac{-3}{2} - \frac{1}{2}\sqrt{3} \\ \frac{-3}{2}\sqrt{3} + \frac{1}{2} ) \end{matrix} \right) + \left( \begin{matrix} 1 \\ 0 \end{matrix} \right) \\ & = \left( \begin{matrix} -\frac{1}{2} - \frac{1}{2}\sqrt{3} \\ -\frac{3}{2}\sqrt{3} + \frac{1}{2} ) \end{matrix} \right) \end{align} $
sehingga $ B^\prime ( -\frac{1}{2} - \frac{1}{2}\sqrt{3} , -\frac{3}{2}\sqrt{3} + \frac{1}{2} ) $
*). Rotasi kedua : $ \theta _ 2 = 30^\circ $ dengan pusat $(a,b) = (-1,3) $.
$ MT = \left( \begin{matrix} \cos (30^\circ ) & - \sin (30^\circ ) \\ \sin (30^\circ ) & \cos (30^\circ ) \end{matrix} \right) = \left( \begin{matrix} \frac{1}{2}\sqrt{3} & - \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2}\sqrt{3} ) \end{matrix} \right) $
Bayangan kedua titik $ B^\prime ( -\frac{1}{2} - \frac{1}{2}\sqrt{3} , -\frac{3}{2}\sqrt{3} + \frac{1}{2} ) $ :
$ \begin{align} \left( \begin{matrix} x^{ \prime \prime } \\ y^{ \prime \prime } \end{matrix} \right) & = ( MT) \times \left( \begin{matrix} x^\prime - a \\ y^\prime - b \end{matrix} \right) + \left( \begin{matrix} a \\ b \end{matrix} \right) \\ & = \left( \begin{matrix} \frac{1}{2}\sqrt{3} & - \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2}\sqrt{3} ) \end{matrix} \right) \times \left( \begin{matrix} -\frac{1}{2} - \frac{1}{2}\sqrt{3} - (-1) \\ -\frac{3}{2}\sqrt{3} + \frac{1}{2} - 3 \end{matrix} \right) + \left( \begin{matrix} -1 \\ 3 \end{matrix} \right) \\ & = \left( \begin{matrix} \frac{1}{2}\sqrt{3} & - \frac{1}{2} \\ \frac{1}{2} & \frac{1}{2}\sqrt{3} ) \end{matrix} \right) \times \left( \begin{matrix} \frac{1}{2} - \frac{1}{2}\sqrt{3} \\ -\frac{3}{2}\sqrt{3} - \frac{5}{2} \end{matrix} \right) + \left( \begin{matrix} -1 \\ 3 \end{matrix} \right) \\ & = \left( \begin{matrix} \frac{1}{4}\sqrt{3} - \frac{3}{4} + \frac{3}{4}\sqrt{3} + \frac{5}{4} \\ \frac{1}{4} - \frac{1}{4}\sqrt{3} - \frac{9}{4} - \frac{5}{4}\sqrt{3} \end{matrix} \right) + \left( \begin{matrix} -1 \\ 3 \end{matrix} \right) \\ & = \left( \begin{matrix} \sqrt{3} + \frac{1}{2} \\ - \frac{7}{4}\sqrt{3} - 2 \end{matrix} \right) + \left( \begin{matrix} -1 \\ 3 \end{matrix} \right) \\ & = \left( \begin{matrix} \sqrt{3} - \frac{1}{2} \\ - \frac{7}{4}\sqrt{3} + 1 \end{matrix} \right) \end{align} $
sehingga $ B^{\prime \prime } ( \sqrt{3} - \frac{1}{2} , - \frac{7}{4}\sqrt{3} + 1 ) $
Jadi, bayangan akhir titik B adalah $ B^{\prime \prime } ( \sqrt{3} - \frac{1}{2} , - \frac{7}{4}\sqrt{3} + 1 ) . \, \heartsuit $.
Demikian pembahasan materi Komposisi Rotasi Sepusat dan contoh-contohnya. Silahkan juga baca materi lain yang berkaitan dengan Komposisi transformasi geometri.