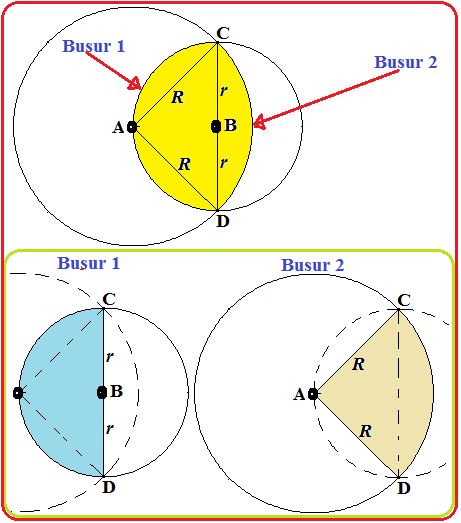
Rumus Keliling Irisan Dua Lingkaran Bentuk 1
Ciri-ciri irisan dua lingkaran bentuk 1 yaitu :
i). Jari-jari kedua lingkaran berbeda,
ii). Titik pusat kedua lingkaran dipisah oleh garis perpotongan lingkaran.
*). Rumus Keliling irisannya :
Keliling irisan $ = \frac{\angle CAD}{360^\circ} . 2 \pi . r + \frac{\angle CBD}{360^\circ} . 2 \pi . r $
Untuk contoh dan cara penurunan rumusnya, silahkan baca link : Keliling Irisan Dua Lingkaran Bentuk 1
i). Jari-jari kedua lingkaran berbeda,
ii). Titik pusat kedua lingkaran dipisah oleh garis perpotongan lingkaran.
Keliling irisan $ = \frac{\angle CAD}{360^\circ} . 2 \pi . r + \frac{\angle CBD}{360^\circ} . 2 \pi . r $
Untuk contoh dan cara penurunan rumusnya, silahkan baca link : Keliling Irisan Dua Lingkaran Bentuk 1
Rumus Keliling Irisan Dua Lingkaran Bentuk 2
Ciri-ciri irisan dua lingkaran bentuk 2 yaitu :
i). Jari-jari kedua lingkaran berbeda,
ii). Titik pusat salah satu lingkaran dilalui oleh garis perpotongan lingkaran.
*). Rumus Keliling irisannya :
Keliling irisan $ = \pi \left( r + \frac{\angle CAD}{180^\circ} . R \right) $
Untuk contoh dan cara penurunan rumusnya, silahkan baca link : Keliling Irisan Dua Lingkaran Bentuk 2
i). Jari-jari kedua lingkaran berbeda,
ii). Titik pusat salah satu lingkaran dilalui oleh garis perpotongan lingkaran.
Keliling irisan $ = \pi \left( r + \frac{\angle CAD}{180^\circ} . R \right) $
Untuk contoh dan cara penurunan rumusnya, silahkan baca link : Keliling Irisan Dua Lingkaran Bentuk 2
Rumus Keliling Irisan Dua Lingkaran Bentuk 3
Ciri-ciri irisan dua lingkaran bentuk 3 yaitu :
i). Jari-jari kedua lingkaran berbeda,
ii). Titik pusat kedua lingkaran ada di sebelah kiri atau kanan dari garis perpotongan lingkaran.
*). Rumus Keliling irisannya :
Keliling irisan $ = \pi \left( \frac{360^\circ - x}{180^\circ} . r + \frac{y}{180^\circ} . R \right) $
Untuk contoh dan cara penurunan rumusnya, silahkan baca link : Keliling Irisan Dua Lingkaran Bentuk 3
i). Jari-jari kedua lingkaran berbeda,
ii). Titik pusat kedua lingkaran ada di sebelah kiri atau kanan dari garis perpotongan lingkaran.
Keliling irisan $ = \pi \left( \frac{360^\circ - x}{180^\circ} . r + \frac{y}{180^\circ} . R \right) $
Untuk contoh dan cara penurunan rumusnya, silahkan baca link : Keliling Irisan Dua Lingkaran Bentuk 3
Rumus Keliling Irisan Dua Lingkaran Bentuk 4
Ciri-ciri irisan dua lingkaran bentuk 4 yaitu :
1). Jari-jari kedua lingkaran sama,
2). dibagi menjadi dua bentuk yaitu :
i). Titik pusat kedua lingkaran berbeda,
ii). titik pusat kedua lingkaran sama.
*). Rumus Keliling irisan titik pusat berbeda
Keliling irisan $ = \frac{\angle CAD}{90^\circ} . \pi . r $
*). Rumus Keliling irisan titik pusat sama
Keliling irisan $ = 2\pi r $
Untuk contoh dan cara penurunan rumusnya, silahkan baca link : Keliling Irisan Dua Lingkaran Bentuk 4
1). Jari-jari kedua lingkaran sama,
2). dibagi menjadi dua bentuk yaitu :
i). Titik pusat kedua lingkaran berbeda,
ii). titik pusat kedua lingkaran sama.
*). Rumus Keliling irisan titik pusat berbeda
*). Rumus Keliling irisan titik pusat sama
Untuk contoh dan cara penurunan rumusnya, silahkan baca link : Keliling Irisan Dua Lingkaran Bentuk 4
Demikian pembahasan materi Rangkuman Rumus Keliling Irisan Dua Lingkaran dan contohnya. Silahkan juga baca materi lain yang berkaitan irisan dua lingkaran dengan mengikuti link yang ada pada artikel terkait disetiap bagian akhir artikel.
