Untuk memudahkan mempelajari materi Konsep Jarak pada Dimensi Tiga atau Bangun Ruang, hal mendasar yang harus kita kuasai terlebih dahulu adalah teorema phytagoras, aturan cosinus pada segitiga, serta Cara Proyeksi Titik, Garis, dan Bidang. Memang tidak semudah mempelajari teorinya dari pada menyelesaikan soal yang berkaitan jarak, karena pada dimensi tiga ini kita harus bisa membayangkan dan menggambarkan jarak yang akan dicari terutama menggunakan proyeksinya. Namun kami yakin, dengan banyak berlatih, pasti kita akan terbiasa dalam menyelesaikan soal yang berkaitan dengan jarak pada dimensi tiga.
Konsep jarak pada dimensi tiga atau bangun ruang yang akan kita bahas di sini adalah jarak antara dua titik, jarak titik ke garis, jarak titik ke bidang, jarak dua garis bersilangan, jarak garis dan bidang yang sejajar, dan jarak dua bidang yang sejajar. Diantara semua jenis konsep jarak yang akan kita pelajari, jarak titik ke titik dan jarak titik ke garis lah yang paling mudah, sementara konsep jarak yang lainnya akan lebih sulit. Makanya teman-teman harus berlatih lebih giat lagi ya, OK !!!^_^!!!
Konsep Jarak pada Dimensi Tiga Secara Umum
Secara umum, yang dimaksud jarak pada dimensi tiga adalah jarak terdekat yang bisa kita peroleh dari konsep
jarak yang akan kita hitung. Jarak terdekat akan kita peroleh ketika terbentuk saling tegak lurus sehingga penghitungannya bisa menggunakan teorema phytagoras.
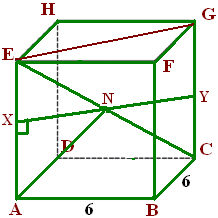
1). Perhatikan gambar kubus berikut ini,
*). Jarak titik E ke NF adalah jarak terdekatnya yaitu jaraknya = panjang EN. Kenapa jaraknya adalah panjang EN ? kok bukan panjang EM? ini disebabkan karena yang ditanyakan adalah jarak titik E ke NF (NF yang dimaksud adalah segmen garis NF saja) bukan jarak E ke garis NF sehingga NF tidak bisa diperpanjang. Artinya jika ditanya jarak terhadap segmen garis tertentu, maka yang kita hitung adalah jarak terdekatnya meskipun tidak membentuk siku-siku seperti gambar (b).
*). Jarak titik E ke garis NF adalah jarak terdekatnya dengan memperpanjang garis FN sehingga menjadi FM, ini artinya jarak terdekatnya membentuk siku-siku. Jarak titik E ke garis NF = panjang EM seperti gambar (c).
Konsep Jarak antara dua titik
Jarak antara dua titik dihitung dengan menggunakan teorema phytagoras biasa, hanya saja kita harus jeli dan pintar
dalam memilih segitiga siku-siku yang melibatkan kedua titik tersebut.
2). Sebuah kubus ABCD.EFGH memiliki panjang rusuk 6 cm. Hitunglah :
a). Jarak titik A ke F,
b). Jarak titik A ke P dengan titik P adalah titik tengah HF,
c). Jarak titik A ke N dengan titik N adalah titik tengah EC,
d). Jarak titik B ke Q , titik Q berada di garis EH dengan EQ = 2QH.
Penyelesaian :
a). Jarak titik A ke F,
$ \begin{align} \text{panjang AF } & = \sqrt{AE^2 + EF^2} \\ & = \sqrt{6^2 + 6^2} \\ & = \sqrt{36 + 36} \\ & = \sqrt{36\times 2} \\ & = 6 \sqrt{ 2} \end{align} $
Jadi, jarak A ke F adalah $ 6\sqrt{2} \, $ cm.
b). Jarak titik A ke P dengan titik P adalah titik tengah HF,
EG adalah diagonal bidang sehingga $ EG = 6 \sqrt{ 2} $
Panjang EP $ \, = \frac{1}{2} EG = \frac{1}{2} \times 6 \sqrt{ 2} = 3 \sqrt{ 2} $
$ \begin{align} \text{panjang AP } & = \sqrt{AE^2 + EP^2} \\ & = \sqrt{6^2 + (3 \sqrt{ 2})^2} \\ & = \sqrt{36 + 18} \\ & = \sqrt{54} \\ & = \sqrt{9\times 6} \\ & = 3 \sqrt{ 6} \end{align} $
Jadi, jarak A ke P adalah $ 3\sqrt{6} \, $ cm.
c). Jarak titik A ke N dengan titik N adalah titik tengah EC,
XY adalah diagonal bidang sehingga $ XY = 6 \sqrt{ 2} $
Panjang XN $ \, = \frac{1}{2} XY = \frac{1}{2} \times 6 \sqrt{ 2} = 3 \sqrt{ 2} $
Panjang AX $ \, = \frac{1}{2} AE = \frac{1}{2} \times 6 = 3 $
$ \begin{align} \text{panjang AN } & = \sqrt{AX^2 + XN^2} \\ & = \sqrt{3^2 + (3 \sqrt{ 2})^2} \\ & = \sqrt{9 + 18} \\ & = \sqrt{27} \\ & = \sqrt{9\times 3} \\ & = 3 \sqrt{ 3} \end{align} $
Jadi, jarak A ke N adalah $ 3\sqrt{3} \, $ cm.
d). Jarak titik B ke Q , titik Q berada di garis EH dengan EQ = 2QH.
BE adalah diagonal bidang sehingga panjang $ BE = 6\sqrt{2} $
*). Menentukan panjang EQ :
$ \begin{align} EQ & = 2QH \\ \frac{EQ}{QH} & = \frac{2}{1} \\ EQ & = \frac{2}{3} EH \\ & = \frac{2}{3} \times 6 \\ & = 4 \end{align} $
*). Menentukan panjang BQ :
$ \begin{align} \text{panjang BQ } & = \sqrt{BE^2 + EQ^2} \\ & = \sqrt{(6 \sqrt{ 2})^2 + 4^2} \\ & = \sqrt{72 + 16} \\ & = \sqrt{88} \\ & = \sqrt{4\times 22} \\ & = 2 \sqrt{22} \end{align} $
Jadi, jarak B ke Q adalah $ 2\sqrt{22} \, $ cm.
Catatan : Segitiga siku-siku yang digunakan untuk masing-masing jawaban adalah salah satu alternatif, artinya teman-teman bisa menggunakan segitiga siku-siku yang lainnya tentu dengan hasil yang sama pula.
Konsep Jarak Titik ke Garis
Misalkan kita mau menghitung jarak titik A ke garis BC, perhatikan gambar berikut ini.
*). gambar (a), Jarak A ke garis BC.
*). gambar (b), Jarak A ke garis BC = panjang AD, dengan AD tegak lurus garis BC. Titik D diperoleh dengan memproyeksikan titik A pada garis BC.
*). gambar (c), untuk menghitung panjang AD, kita buat segitiga bantuan dengan menghubungkan AB dan AC sehingga terbentuk segitiga ABC.
Ada beberapa cara dalam menyelesaikan konsep jarak titik ke garis, diantaranya menggunakan :
i). perbandingan luas segitiga.
Cara ini digunakan jika segitiga yang terbentuk siku-siku di A atau panjang semua segitiganya adalah bilangan bulat.
ii). teorema phytagoras.
Cara ini bida digunakan untuk semua tipe soal jarak titik ke garis.
iii). aturan cosinus.
Cara ini digunakan sebagai alternatif lain dari dua cara sebelumnya. Kita akan mencari nilai cos dari sudut B atau C, kemudian kita cari lagi nilai sin sudut B atau C dengan segitiga baru.
*). gambar (b), Jarak A ke garis BC = panjang AD, dengan AD tegak lurus garis BC. Titik D diperoleh dengan memproyeksikan titik A pada garis BC.
*). gambar (c), untuk menghitung panjang AD, kita buat segitiga bantuan dengan menghubungkan AB dan AC sehingga terbentuk segitiga ABC.
Ada beberapa cara dalam menyelesaikan konsep jarak titik ke garis, diantaranya menggunakan :
i). perbandingan luas segitiga.
Cara ini digunakan jika segitiga yang terbentuk siku-siku di A atau panjang semua segitiganya adalah bilangan bulat.
ii). teorema phytagoras.
Cara ini bida digunakan untuk semua tipe soal jarak titik ke garis.
iii). aturan cosinus.
Cara ini digunakan sebagai alternatif lain dari dua cara sebelumnya. Kita akan mencari nilai cos dari sudut B atau C, kemudian kita cari lagi nilai sin sudut B atau C dengan segitiga baru.
3). Pada kubus ABCD.EFGH dengan panjang rusuk 8 cm. Tentukan jarak titik E ke garis AG?
Penyelesaian :
Cara I : Menggunakan luas segitiga,
Luas segitiga AEG dapat dihitung dari dua cara yaitu dengan alasnya AG dan tingginya EP, serta alasnya EA dan tingginya EG yang keduanya memiliki luas yang sama.
$ \begin{align} \text{Luas AEG (alas AG) } & = \text{Luas AEG (alas EA) } \\ \frac{1}{2} \times AG \times EP & = \frac{1}{2} \times EA \times EG \\ AG \times EP & = EA \times EG \\ 8\sqrt{3} \times EP & = 8 \times 8\sqrt{2} \\ EP & = \frac{8 \times 8\sqrt{2}}{8\sqrt{3} } \\ & = \frac{ 8\sqrt{2}}{\sqrt{3} } \\ & = \frac{ 8}{3 } \sqrt{6} \end{align} $
Jadi, jarak E ke garis AG adalah $ \frac{ 8}{3 } \sqrt{6} \, $ cm.
Cara II : Menggunakan teorema phytagoras,
Misalkan panjang $ AP = x , \, $ maka panjang $ PG = AG - AP = 8\sqrt{3} - x $
Perhatikan segitiga EAP, $ EP^2 = EA^2 - AP^2 $
Perhatikan segitiga EGP, $ EP^2 = EG^2 - GP^2 $
Kedua panjang EP adalah sama, sehingga kita peroleh :
$ \begin{align} \text{ (segitiga EAP) } EP^2 & = \text{ (segitiga EGP) } EP^2 \\ EA^2 - AP^2 & = EG^2 - GP^2 \\ 8^2 - x^2 & = (8\sqrt{2})^2 - (8\sqrt{3} - x)^2 \\ 64 - x^2 & = 128 - (192 - 16\sqrt{3}x + x^2) \\ 64 - x^2 & = 128 - 192 + 16\sqrt{3}x - x^2 \\ 64 & = -64 + 16\sqrt{3}x \\ 16\sqrt{3}x & = 128 \\ x & = \frac{128}{16\sqrt{3}} \\ x & = \frac{8}{3}\sqrt{3} \end{align} $
Menentukan panjang EP :
$ \begin{align} EP^2 & = EA^2 - AP^2 \\ & = 8^2 - (\frac{8}{3}\sqrt{3})^2 \\ & = 64 - (\frac{64}{3} ) \\ EP^2 & = \frac{128}{3} \\ EP & = \sqrt{ \frac{128}{3} } = \frac{\sqrt{128}}{\sqrt{3}} = \frac{8\sqrt{2}}{\sqrt{3}} = \frac{8 }{3} \sqrt{6} \end{align} $
Jadi, jarak E ke garis AG adalah $ \frac{ 8}{3 } \sqrt{6} \, $ cm.
Cara III : Menggunakan Aturan cosinus,
*). Perhatikan segitiga EAG, kita terapkan aturan cosinus pada sudut A.
$ EG^2 = AE^2 + AG^2 - 2 . AE. AG \cos A \rightarrow \cos A = \frac{AE^2 + AG^2- EG^2}{2 . AE. AG} $.
Menentukan nilai cos A :
$ \begin{align} \cos A & = \frac{AE^2 + AG^2- EG^2}{2 . AE. AG} \\ & = \frac{8^2 + (8\sqrt{3})^2- (8\sqrt{2})^2}{2 . 8. (8\sqrt{3})} \\ & = \frac{64 + 192- 128}{2 . 8. (8\sqrt{3})} \\ & = \frac{128}{2 . 8.8\sqrt{3}} \\ & = \frac{1}{ \sqrt{3}} \end{align} $
Menentukan nilai sin A , menggunakan identitas trigonometri :
$ \sin ^2 A + \cos ^2 A = 1 \rightarrow \sin ^2 A + (\frac{1}{ \sqrt{3}})^2 = 1 \rightarrow \sin ^2 A + \frac{1}{ 3} = 1 $
$ \rightarrow \sin ^2 A = \frac{2}{ 3} \rightarrow \sin A = \sqrt{\frac{2}{ 3} } = \frac{1}{3}\sqrt{6} $
Menentukan panjang EP, perhatikan segitiga EAP :
$ \begin{align} \sin A & = \frac{de}{mi} \\ \frac{1}{3}\sqrt{6} & = \frac{EP}{EA} \\ \frac{1}{3}\sqrt{6} & = \frac{EP}{8} \\ \frac{8}{3}\sqrt{6} & = EP \end{align} $
Jadi, jarak E ke garis AG adalah $ \frac{ 8}{3 } \sqrt{6} \, $ cm.
Catatan :
*). Tidak semua soal bisa dikerjakan dengan ketiga cara diatas. Namun untuk cara II dan Cara III bisa diterapkan kesemua tipe soal konsep jarak titik ke garis.
*). Penghitungan jarak titik ke garis juga bisa menggunakan konsep vektor, silahkan baca artikelnya pada "aplikasi vektor : jarak titik ke garis"
4). Diketahui titik P ada ditengah-tengah garis EA pada kubus ABCD.EFGH dengan panjang rusuk 10 cm. Tentukan jarak titik P ke garis BH?
Penyelesaian :
*). Menentukan panjang sisi-sisi segitiganya :
panjang PB = PH = $ \sqrt{PA^2 + PB^2} = \sqrt{5^2 + 100^2} = 5\sqrt{5} $
Karena segitiga PBH samakaki, maka letak N terletak ditengah BH.
Panjang $ BN = \frac{1}{2} BH = \frac{1}{2} \times 10\sqrt{3} = 5\sqrt{3} $
Menentukan panjang PN, menggunakan segitiga PBN
$ \begin{align} PN & = \sqrt{PB^2 - BN^2} \\ & = \sqrt{(5\sqrt{5})^2 - (5\sqrt{3})^2} \\ & = 5\sqrt{2} \end{align} $
Jadi, jarak P ke garis BH adalah $ 5\sqrt{2} \, $ cm.
5). Pada limas segiempat beraturan T.ABCD memiliki rusuk alas $ 3\sqrt{2} \, $ cm dan rusuk tegaknya 8 cm. Tentukan jarak titik A ke TC?
Penyelesaian :
Jarak A ke garis TC, kita gunakan segitiga ATC sebagai bantuannya.
Panjang AC pada segitiga ABC :
$ AC = \sqrt{AB^2 + BC^2 } = \sqrt{ (3\sqrt{2})^2 + (3\sqrt{2})^2 } = \sqrt{36} = 6 $
Untuk menghitung jarak A ke TC = panjang AE, banyak metode yang bisa kita terapkan, misalnya metode phytagoras seperti contoh 3 dengan memisalkan $ CE = x \, $. Bisa juga menggunakan metode aturan cosinus pada sudut C atau T. Pada pembahasan ini kita akan menggunakan metode luas segitiga karena sisi-sisi segitiganya berupa bilangan bulat dengan luasan rumus Heron dan metode luasan biasa.
Cara I : Luas segitiga rumus Heron,
Luas segitiga $ \, = \sqrt{s(s-a)(s-b)(s-c)} \, $ dengan $ s = \frac{1}{2}(a+b+c) $.
Segitiga ATC dengan sisi-sisi 6, 8, 8.
$ s = \frac{1}{2}(6 + 8 + 8) = \frac{1}{2}(22) = 11 $
$ \begin{align} \text{Luas ATC } & = \sqrt{s(s-a)(s-b)(s-c)} \\ & = \sqrt{11(11-6)(11-8)(11-8)} = \sqrt{11.5.3.3} = 3\sqrt{55} \end{align} $
Luas segitiga ATC juga dapat dihitung dengan rumus :
$ \text{Luas ATC } = \frac{1}{2} a t = \frac{1}{2}.TC . AE = \frac{1}{2}.8 . AE = 4AE $
*). Menentukan panjang AE dengan kedua luas ATC yang sama.
$ \begin{align} \text{Luas ATC } & = \text{Luas ATC } \\ \frac{1}{2}.TC . AE & = \sqrt{s(s-a)(s-b)(s-c)} \\ 4AE & = 3\sqrt{55} \\ AE & = \frac{3}{4} \sqrt{55} \end{align} $
Jadi, jarak A ke garis TC adalah $ \frac{3}{4} \sqrt{55} \, $ cm.
Cara II : Luas segitiga rumus biasa,
Perhatikan gambar (c),
Panjang TF dari segitiga TFC,
$ TF = \sqrt{TC^2 - FC^2 } = \sqrt{8^2 - 3^2 } = \sqrt{64 - 9 } = \sqrt{ 55} $
Luas segitiga ATC,
$ \text{Luas ATC } = \frac{1}{2} a t = \frac{1}{2}.AC . TF = \frac{1}{2}. 6 . \sqrt{ 55} = 3\sqrt{ 55} $
*). Menentukan panjang AE dengan kedua luas ATC yang sama.
$ \begin{align} \text{Luas ATC } & = \text{Luas ATC } \\ \frac{1}{2}.TC . AE & = \frac{1}{2}.AC . TF \\ 4AE & = 3\sqrt{55} \\ AE & = \frac{3}{4} \sqrt{55} \end{align} $
Jadi, jarak A ke garis TC adalah $ \frac{3}{4} \sqrt{55} \, $ cm.
6). Tentukan jarak titik A ke garis EF pada kubus ABCD.EFGH yang memiliki panjang rusuk 10 cm?
Penyelesaian :
Untuk konsep jarak lainnya pada dimensi tiga, silahkan baca pada artikel : jarak titik dan bidang pada dimensi tiga, jarak dua garis bersilangan pada dimensi tiga, jarak antara garis dan bidang pada dimensi tiga.
Bagaimana dengan materi Konsep Jarak pada Dimensi Tiga atau Bangun Ruang ini, pasti seru ya!!!. Memang tidak mudah untuk mengerjakan soal-soal yang berkaitan dengan jarak pada dimensi tiga. Semuanya butuh latihan dan berlatih terus secara kontinu untuk mempelajarinya. Percayalah, semuanya pasti bisa, tidak ada yang tidak mungkin di dunia ini. (sok menghibur diri saya sebagai penulis, karena menurut saya juga sulit kok mempelajari dimensi tiga, apalagi berkaitan dengan soal-soal seleksi masuk PTN. ^_^). Semoga bermanfaat materi pada artikel ini untuk kita semua.
