Volume Benda Putar Menggunakan Integral

         Blog Koma - Salah satu penggunaan integral selain menghitung luas daerah juga digunakan untuk menghitung volume benda putar. Pada artikel ini kita akan membahas artikel Volume Benda Putar Menggunakan Integral. Volume benda putar disini maksudnya suatu daerah yang dibatasi oleh beberapa kurva kemudian diputar terhadap suatu garis tertentu yang biasanya diputar mengelilingi sumbu X atau sumbu Y dengan satu putaran penuh yaitu $ 360^\circ $ . Namun untuk tingkat kuliah, khususnya pada matakuliah kalkulus, daerah tersebut tidak hanya diputar terhadap sumbu X atau sumbu Y saja, akan tetapi bisa diputar terhadap garis lain.

         Berikut ilustrasi volume benda putar menggunakan integral dengan memutar suatu daerah mengelilingi sumbu X seperti gambar berikut ini.

Dari gambar ilustrasi di atas, gambar pertama daerah berupa segitiga diputar mengelilingi sumbu X sehingga terbentuk bangun ruang kerucut, dan gambar kedua daerah berupa setengah lingkaran diputar mengelilingi sumbu X sehingga terbentuk bangun ruang bola.

         Volume Benda Putar Menggunakan Integral secara umum menggunakan dua metode dalam perhitungannya yaitu metode cakram dan metode kulit tabung. Untuk metode cakram memiliki ciri arah putaran sesuai dengan batasan integralnya, misalkan jika daerah diputar terhadap sumbu X maka batasannya juga ada pada sumbu X. Sedangkan metode kulit tabung dalam volume benda putar memiliki ciri arah putaran berbeda dengan batasan integralnya, misalkan daerah diputar terhadap sumbu Y tetapi batasnya ada di sumbu X. Seperti luas suatu daerah, volume benda putar juga ada yang dibatasi satu kurva saja dan ada dibatasi dua kurva.

Metode Cakram :

Volume Benda Putar Mengelilingi Sumbu X

Perhatikan gambar berikut ini,

Volume benda putar yang terjadi dari daerah yang dibatasi oleh $ y = f(x) $, sumbu X, garis $ x = a$, dan garis $ x = b $ diputar mengelilingi sumbu X sejauh $ 360^\circ$, volumenya adalah
Volume $ = \pi \int \limits_a^b y^2 dx = \pi \int \limits_a^b [f(x)]^2 dx $

Contoh soal volume benda putar :
1). Tentukan volume benda putar yang terjadi jika bidang datar yang dibatasi oleh kurva $ y = x $, sumbu X, dan garis $ x = 3 $ diputar mengelilingi sumbu X sejauh $ 360^\circ $. ?

Penyelesaian :
*). gambar benda putar yang terbentuk :

baca materi : Persamaan Garis Lurus dan Grafiknya.
*). Menentukan volumenya,
$\begin{align} V & = \pi \int \limits_a^b [f(x)]^2 dx \\ & = \pi \int \limits_0^3 [x]^2 dx \\ & = \pi [\frac{1}{3}x^3]_0^3 \\ & = \pi ( [\frac{1}{3}.3^3] - [\frac{1}{3}.0^3] ) \\ & = \pi ( [9] - [0] ) \\ & = 9 \pi \end{align} $
Jadi, volume benda putar yang terbentuk adalah $ 9 \pi $ satuan volume.

Volume Benda Putar Mengelilingi Sumbu Y

Perhatikan gambar berikut ini,

Jika daerah yang dibatasi oleh $ x = f(y)$, sumbu Y, garis $ y = a$, dan garis $ y = b $ diputar mengelilingi sumbu Y sejauh $ 360^\circ$, volume benda putarnya adalah
Volume $ = \pi \int \limits_a^b x^2 dy = \pi \int \limits_a^b [f(y)]^2 dy $

Contoh soal :
2). Tentukan volume benda putar yang terjadi jika daerah yang dibatasi oleh sumbu Y, kurva $ y = x^2$, garis $ y = 2$, dan garis $ y = 5 $ diputar mengelilingi sumbu Y.

Penyelesaian :
*). Gambarnya,

baca materi : Sketsa dan Menggambar Grafik Fungsi Kuadrat.
*). Menentukan volumenya,
$\begin{align} V & = \pi \int \limits_a^b [f(y)]^2 dy \\ & = \pi \int \limits_2^5 [\sqrt{y}]^2 dy \\ & = \pi \int \limits_2^5 y dy \\ & = \pi [ \frac{1}{2}y^2]_2^5 \\ & = \pi ( [ \frac{1}{2}.5^2] - [ \frac{1}{2}.2^2]) \\ & = \frac{21}{2}\pi \end{align} $
Jadi, volume benda putar yang terbentuk adalah $ \frac{21}{2}\pi $ satuan volume.

Volume Benda Putar dibatasi Dua Kurva

*). Diputar terhadap sumbu X

Dimisalkan T adalah daerah tertutup yang dibatasi oleh kurva-kurva $ y_1 = f(x) $ dan $ y_2 = g(x) $ dengan $ | f(x) | \geq | g(x) | $ pada interval $ a \leq x \leq b$. Daerah yang terbentuk diputar mengelilingi sumbu X sejauh $ 360^\circ $ sehingga terbentuk suatu benda putar yang tengahnya kosong. Perhatikan gambar di atas. Volume benda yang terbentuk dari daerah yang dibatasi oleh kurva $ y_1 = f(x), y_2 = g(x)$, garis $ x = a $ dan $ x = b $ adalah
Volume $ \, = \pi \int \limits_a^b (y_1)^2 - (y_2)^2 dx = \pi \int \limits_a^b [f(x)]^2 - [g(x)]^2 dx $.

*). Diputar terhadap sumbu Y

Dimisalkan U adalah daerah tertutup yang dibatasi oleh kurva-kurva $ x_1 = f(y) $ dan $ x_2 = g(y) $ dengan $ | f(y) | \geq | g(y) | $ pada interval $ a \leq x \leq b$. Daerah yang terbentuk diputar mengelilingi sumbu Y sejauh $ 360^\circ $ sehingga terbentuk suatu benda putar yang tengahnya kosong. Perhatikan gambar di atas. Volume benda yang terbentuk adalah
Volume $ \, = \pi \int \limits_a^b (x_1)^2 - (x_2)^2 dy = \pi \int \limits_a^b [f(y)]^2 - [g(y)]^2 dy $.

Catatan :
Cara mengurangkannya yaitu kurva terjauh dikurangkan kurva terdekat terhadap sumbu putar.

Contoh soal :
3). Tentukan volume benda putar yang terjadi, jika daerah yang dibatasi oleh kurva $ y = 6x - x^2 $ dan $ y = x $ diputar mengelilingi sumbu X sejauh $ 360^\circ$

Penyelesaian :
*). menentukan titik ptong kedua kurva :
$ \begin{align} y_1 & = y_2 \\ x & = 6x - x^2 \\ x^2 - 5x & = 0 \\ x(x-5) & = 0 \\ x = 0 \vee x & = 5 \end{align} $
artinya batas integralnya dari 0 sampai 5.
*). Gambar daerahnya,

*). Menentukan volumenya,
$\begin{align} V & = \pi \int \limits_a^b [f(x)]^2 - [g(x)]^2 dx \\ & = \pi \int \limits_0^5 [6x - x^2]^2 - [x]^2 dx \\ & = \pi \int \limits_0^5 ( x^4 -12x^3 + 35x^2) dx \\ & = \pi [ \frac{1}{5}x^5 -3x^4 + \frac{35}{3}x^3]_0^5 \\ & = 208\frac{1}{3} \pi \end{align} $
Jadi, volume benda putar yang terbentuk adalah $ 208\frac{1}{3} \pi $ satuan volume.

4). Hitunglah volume benda putar yang terjadi jika daerah yang dibatasi oleh kurva $ y = x^2, y = 3x^2$, dan $ y = 3 $ di kuadran pertama diputar mengelilingi sumbu Y sejauh $ 360^\circ$.

Penyelesaian :
*). gambar daerahnya,

*). Mengubah fungsi menjadi $ x = f(y) $,
fungsi $ y = x^2 \rightarrow x_1 = \sqrt{y} $
fungsi $ y = 3x^2 \rightarrow x_2 = \sqrt{\frac{1}{3}y} $
*). Menentukan volumenya,
$\begin{align} V & = \pi \int \limits_a^b [f(y)]^2 - [g(y)]^2 dy \\ & = \pi \int \limits_0^3 [\sqrt{y}]^2 - [\sqrt{\frac{1}{3}y}]^2 dy \\ & = \pi \int \limits_0^3 (y - \frac{1}{3}y) dy \\ & = \pi \int \limits_0^3 \frac{2}{3}y dy \\ & = \pi [\frac{2}{6}y^2]_0^3 \\ & = \pi [\frac{1}{3}y^2]_0^3 \\ & = \pi ([\frac{1}{3}.3^2]- [\frac{1}{3}.0^2] ) \\ & = \pi ([3]- [0]) \\ & = 3 \pi \end{align} $
Jadi, volume benda putar yang terbentuk adalah $ 3 \pi $ satuan volume.

Metode Kulit Tabung :

Volume benda putar mengelilingi sumbu X atau Y

*). Mengelilingi sumbu Y dan batas di sumbu X

Volume benda putar yang dibatasi oleh kurva $ y = f(x) , \, x = a, \, x = b, \, $ dan sumbu X diputar terhadap sumbu Y sejauh $ 360^\circ \, $ adalah
Volume $ \, = 2\pi \int \limits_a^b xy dx = 2\pi \int \limits_a^b xf(x) dx $

*). Mengelilingi sumbu X dan batas di sumbu Y

Volume benda putar yang dibatasi oleh kurva $ x = f(y) , \, y = a, \, y = b, \, $ dan sumbu Y diputar terhadap sumbu X sejauh $ 360^\circ \, $ adalah
Volume $ \, = 2\pi \int \limits_a^b xy dy = 2\pi \int \limits_a^b f(y) . y dy $

Catatan :
Metode kulit tabung ini kita pakai apabila kita kesulitan dalam mengubah bentuk fungsi $ y = f(x) \, $ menjadi $ x = f(y) \, $ atau sebaliknya.

Contoh soal :
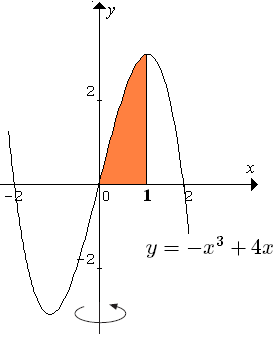
5). Tentukan volume benda putar yang dibatasi oleh kurva $ y = -x^3 + 4x , \, x = 0, \, x = 1 , \, $ dan sumbu X yang diputar mengelilingi sumbu Y sejauh $ 360^\circ $ . ?

Penyelesaian :
*). Gambar daerahnya,

Karena diputar mengelilingi sumbu Y, dengan metode cakram seharusnya batasnya ada pada sumbu Y dan fungsi kita ubah menjadi bentuk $ x = f(y) $. Hanya saja fungsi dari kurvanya $ y = -x^3 + 4x \, $ yang akan sangat sulit bagi kita untuk mengubahnya menjadi bentuk $ x = f(y) $ , dalam hal ini metode cakram sulit kita terapkan untuk menghitung volume benda putarnya. Sehingga yang termudah kita gunakan metode kulit tabung.
*). Menentukan volumenya,
$\begin{align} V & = 2\pi \int \limits_a^b xy dx \\ & = 2\pi \int \limits_0^1 x(-x^3 + 4x) dx \\ & = 2\pi \int \limits_0^1 (-x^4 + 4x^2) dx \\ & = 2\pi [\frac{-1}{5}x^5 + \frac{4}{3}x^3]_0^1 \\ & = 2\pi ( [\frac{-1}{5}.1^5 + \frac{4}{3}.1^3] - [\frac{-1}{5}.0^5 + \frac{4}{3}.0^3]) \\ & = 2\pi ( [\frac{-1}{5} + \frac{4}{3} ] - [0]) \\ & = 2\pi ( \frac{-3}{15} + \frac{20}{15} ) \\ & = 2\pi ( \frac{17}{15} ) \\ & = \frac{34}{15} \pi \\ & = 2\frac{4}{15} \pi \end{align} $
Jadi, volume benda putar yang terbentuk adalah $ 2\frac{4}{15} \pi $ satuan volume.

Volume Benda Putar dibatasi dua kurva Metode Kulit Tabung

*). Mengelilingi sumbu Y dan batas di sumbu X
Volume benda putar yang dibatasi oleh kurva $ y = f(x) , \, y = g(x) , \, x = a, \, x = b, \, $ dan sumbu X diputar terhadap sumbu Y sejauh $ 360^\circ \, $ dengan $ |f(x)| \geq |g(x)| \, $ adalah
Volume $ \, = 2\pi \int \limits_a^b xy dx = 2\pi \int \limits_a^b x[f(x) - g(x)] dx $

*). Mengelilingi sumbu X dan batas di sumbu Y
Volume benda putar yang dibatasi oleh kurva $ x = f(y) , \, x = g(y) , \, y = a, \, y = b, \, $ dan sumbu Y diputar terhadap sumbu X sejauh $ 360^\circ \, $ dengan $ |f(y)| \geq |g(y)| \, $ adalah
Volume $ \, = 2\pi \int \limits_a^b xy dy = 2\pi \int \limits_a^b [f(y) - g(y)] y dy $

Contoh soal :
6). Tentukan volume benda putar yang dibatasi oleh kurva $ y = \frac{1}{3}x^2 , \, y = x , \, x = 0, \, x = 2 , \, $ dan sumbu X yang diputar mengelilingi sumbu Y sejauh $ 360^\circ $ . ?

Penyelesaian :
*). Gambar daerahnya,

*). Menentukan volumenya,
$\begin{align} V & = 2\pi \int \limits_a^b x[f(x) - g(x)] dx \\ & = 2\pi \int \limits_0^2 x[x - \frac{1}{3}x^2] dx \\ & = 2\pi \int \limits_0^2 (x^2 - \frac{1}{3}x^3) dx \\ & = 2\pi [\frac{1}{3}x^3 - \frac{1}{12}x^4]_0^2 \\ & = 2\pi ( [\frac{1}{3}.2^3 - \frac{1}{12}.2^4] - [\frac{1}{3}.0^3 - \frac{1}{12}.0^4] ) \\ & = 2\pi ( [\frac{8}{3} - \frac{4}{3} ] - [0] ) \\ & = 2\pi ( [\frac{4}{3} ] ) \\ & = \frac{8}{3} \pi \\ & = 2\frac{2}{3} \pi \end{align} $
Jadi, volume benda putar yang terbentuk adalah $ 2\frac{2}{3} \pi $ satuan volume.

       Volume benda putar menggunakan integral yang dibahas pada artikel ini memang sederhana dan merupakan konsep dasar yang harus dikuasai serta dipahami dengan baik. Artinya untuk tipe soal yang sulitpun pengerjaannya akan melalui proses yang sama seperti contoh-contoh soal pada materi ini. Dari hampir semua contoh yang ada pada volume benda putar, hal mendasar yang harus kita pahami terlebih dahulu adalah menggambar kurva atau grafik dari fungsi yang ada, setelah itu baru menguasai cara mengintegralkan fungsi aljabar. Semoga materi ini berguna untuk kita semua.