Irisan Dua Lingkaran

         Blog Koma - Irisan Dua Lingkaran merupakan materi matematika peminatan. Materi yang akan dipelajari pada irisan dua lingkaran yaitu "kedudukan dua lingkaran", "garis singgung persekutuan lingkaran", "luas dan keliling irisan dua lingkaran",  "kuasa pada lingkaran", dan "berkas lingkaran". Untuk memudahkan dalam mempelajari irisan dua lingkaran, kita harus menguasai materi "jarak dua titik", "panjang busur dan luas juring", dan "aturan cosinus pada segitiga". Berikut akan dijelaskan sedikit materi dasar yang dibutuhkan dalam mempelajari irisan dua lingkaran.

Jarak Dua titik

       Misalkan ada titik A($x_1,y_1$) dan titik B($x_2,y_2$), jarak kedua titik A dan B adalah :

Jarak = $ |AB| = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 } $

Konsep jarak dua titik ini akan digunakan pada materi "kedudukan dua lingkaran" dan menghitung luas serta keliling irisan lingkaran.

Contoh :
Tentukan jarak titik A(1,2) dan titik B(-2, 6) !
Penyelesaian :
*). Jarak titik A dan B kita simbolkan $ |AB| $ :
$ \begin{align} |AB| & = \sqrt{(x_2-x_1)^2 + (y_2-y_1)^2 } \\ & = \sqrt{(-2-1)^2 + (6-2)^2 } \\ & = \sqrt{(-3)^2 + (4)^2 } \\ & = \sqrt{9 + 16 } \\ & = \sqrt{25 } \\ & = 5 \end{align} $
Jadi, jarak A dan B adalah 5 satuan.

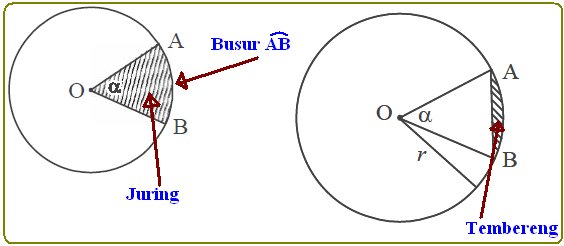
Panjang busur, Luas juring, dan Luas Tembereng

       Berikut gambar busur, juring, dan tembereng pada lingkaran

Rumus dasarnya :
$\begin{align} \text{Panjang Busur AB } & = \frac{\alpha}{360^\circ} \times 2 \pi r \\ \text{Luas Juring AOB } & = \frac{\alpha}{360^\circ} \times \pi r^2 \\ \text{Luas Tembereng AB } & = \text{Luas Juring AOB } - \text{Luas Segitiga AOB } \end{align} $

dimana $ r = \, $ jari-jari lingkaran dan $ \pi = \frac{22}{7} = 3,14 $

Konsep panjang busur, luas juring, dan luas tembereng digunakan untuk materi "luas dan keliling irisan lingkaran".

Contoh :
Perhatikan Gambar di bawah ini. Diketahui panjang jari-jari OA = 10 cm. Jika besar $ \angle AOB = 60^\circ $ , hitunglah :

a). panjang AB ;
b). luas juring OAB;
c). luas tembereng AB.
Penyelesaian :
a). Panjang busur AB ,
$ \begin{align} \text{panjang busur AB } & = \frac{\alpha}{360^\circ} \times 2 \pi r \\ & = \frac{60^\circ}{360^\circ} \times 2 \times 3,14 \times 10 \\ & = \frac{1}{6} \times 62,8 \\ & = 10, 47 \end{align} $
b). luas juring OAB ,
$ \begin{align} \text{Luas Juring AOB } & = \frac{\alpha}{360^\circ} \times \pi r^2 \\ & = \frac{60^\circ}{360^\circ} \times 3,14 \times 10^2 \\ & = \frac{1}{6} \times 314 \\ & = 52,33 \end{align} $
*). Menentukan luas segitiga AOB :
Karena $ \angle AOB = 60^\circ $ , maka segitiga AOB sama sisi. Luas segitiga sama sisi adalah $ \text{Luas } = \frac{1}{4} a^2 \sqrt{3} $ dengan $ a \, $ adalah sisi segitiga atau di sini nilai $ a \, $ sama dengan jari-jari.
$\begin{align} \text{Luas Segitiga AOB } & = \frac{1}{4} a^2 \sqrt{3} \\ & = \frac{1}{4} 10^2 \sqrt{3} \\ & = 25\sqrt{3} = 43,30 \end{align} $
c). luas tembereng AB
$\begin{align} \text{Luas Tembereng AB } & = \text{Luas Juring AOB } - \text{Luas Segitiga AOB } \\ & = 52,33 - 43,30 \\ & = 9,03 \end{align} $
Jadi, panjang busur AB = 10,47 cm, luas juring AOB = 52,33 cm$^2$ , dan luas tembereng AB = 9,03 cm$^2$.

Aturan Cosinus pada segitiga

       Aturan Cosinus digunakan untuk menentukan besarnya sudut suatu segitiga. Misalkan ada segitiga sperti dibawah ini :

Rumus aturan cosinusnya adalah :
$ BC^2 = AC^2 + AB^2 - 2. AC. AB . \cos A \, $ atau $ \cos A = \frac{AC^2 + AB^2 - BC^2}{2.AC.AB} $

Contoh :
Diketahui segitiga seperti gambar berikut.

Tentukan besarnya sudut BAC?
Penyelesaian :
*). Menentukan nilai cosinus sudut BAC :
$ \begin{align} \cos A & = \frac{AC^2 + AB^2 - BC^2}{2.AC.AB} \\ & = \frac{4^2 + 6^2 - 5^2}{2.4.6} \\ & = \frac{16 + 36 - 25}{48} \\ \cos A & = \frac{27}{48} \\ \cos A & = \frac{9}{16} \end{align} $
*). Menentukan besar sudut BAC :
$ \begin{align} \cos \angle BAC & = \frac{9}{16} \\ \angle BAC & = arc \cos \frac{9}{16} \\ \angle BAC & = 55,77^\circ \end{align} $
Jadi, besar sudut BAC adalah $ 55,77^\circ $ .

Cara Menentukan besarnya sudut yang diketahui nilai cosinusnya menggunakan kalkulator

       Untuk bisa menghitung besarnya sudut yang diketahui nilai cosinusnya, kita harus menggunakan kalkulator scientific.
Lankah-langkahnya :
Tekan tombol SHIFT --->>> tekan tombol COS
--->>> tekan ANGKAnya --->>> tekan =

Contoh :
Tentukan besarnya sudut BAC jika diketahui $ \cos \angle BAC = \frac{9}{16} $ !
Penyelesaian :
Tekan tombol SHIFT --->>> tekan tombol COS --->>> tekan $ \frac{9}{16} \, $ --->>> tekan = ,
maka hasilnya $ 55,77 $ . Ini artinya besar sudut BAC adalah $ 55,77^\circ $ .