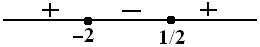Penjelasan Tanda Ketaksamaan
Pada pertidaksamaan memuat tanda ketaksamaan : $ <, \, >, \, \leq , \, \geq, \, \neq . \, $ Berikut penjelasannya masing-masing,
$\spadesuit $ Tanda $ < \, $ dibaca kurang dari atau lebih kecil
$ x < 2 \, $ artinya nilai $ x $ yang memenuhi harus kurang dari 2 dan dua tidak boleh ikut.
Himpunannya : $ x = \{ ...,-1,0,1 \} \, $ ,
garis bilangannya :
$\spadesuit $ Tanda $ \leq \, $ dibaca kurang dari sama dengan atau lebih kecil sama dengan
$ x \leq 2 \, $ artinya nilai $ x $ yang memenuhi harus lebih kecil dan sama dengan dari 2 (dua boleh ikut).
Himpunannya : $ x = \{ ...,-1,0,1,2 \} \, $ ,
garis bilangannya :
$\spadesuit $ Tanda $ > \, $ dibaca lebih dari atau lebih besar
$ x > -3 \, $ artinya nilai $ x $ yang memenuhi harus lebih besar dari -3 (-3 tidak boleh ikut).
Himpunannya : $ x = \{ -2,-1,0,1,... \} \, $ ,
garis bilangannya :
$\spadesuit $ Tanda $ \geq \, $ dibaca lebih dari sama dengan atau lebih besar sama dengan
$ x \geq -3 \, $ artinya nilai $ x $ yang memenuhi harus lebih besar dan sama dengan dari -3 (-3 boleh ikut).
Himpunannya : $ x = \{ -3,-2,-1,0,1,... \} \, $ ,
garis bilangannya :
$\spadesuit $ Tanda $ < \, $ dibaca kurang dari atau lebih kecil
$ x < 2 \, $ artinya nilai $ x $ yang memenuhi harus kurang dari 2 dan dua tidak boleh ikut.
Himpunannya : $ x = \{ ...,-1,0,1 \} \, $ ,
garis bilangannya :
$ x \leq 2 \, $ artinya nilai $ x $ yang memenuhi harus lebih kecil dan sama dengan dari 2 (dua boleh ikut).
Himpunannya : $ x = \{ ...,-1,0,1,2 \} \, $ ,
garis bilangannya :
$ x > -3 \, $ artinya nilai $ x $ yang memenuhi harus lebih besar dari -3 (-3 tidak boleh ikut).
Himpunannya : $ x = \{ -2,-1,0,1,... \} \, $ ,
garis bilangannya :
$ x \geq -3 \, $ artinya nilai $ x $ yang memenuhi harus lebih besar dan sama dengan dari -3 (-3 boleh ikut).
Himpunannya : $ x = \{ -3,-2,-1,0,1,... \} \, $ ,
garis bilangannya :
$2x +1 < 0, \, \frac{3x+4}{x-2} \geq 6 , \, x^2 - 3x + 4 > 0 , $
$ \sqrt{2x+5} \leq x - 1 , \, | x+5| - 3x \geq 7 , \, x^2 - x + 2 \neq 0 $
Penyelesaian Pertidaksamaan
Penyelesaian yang dimaksud adalah semua nilai variabel yang ada (misal $x $) yang memenuhi pertidaksamaan tersebut.
Misal, penyelesaian pertidaksamaan $ -2x + 4 < 0 \, $ adalah $ x > 2, \, $ artinya untuk semua nilai $ x $ yang memenuhi $ x > 2 \, $ pasti juga akan memenuhi
$ -2x+4 < 0 . \, $ Contoh, $ x = 3 \, $ , maka $ -2.(3) + 4 = -2 < 0 $
Cara menentukan tanda $+$ atau $ - $ pada garis bilangan
Untuk menentukan tanda $ + $ atau $ - $ pada garis bilangan, nolkan ruas kanan pertidaksamaan, kemudian pilih angka
dari selang yang terbentuk pada garis bilangan dan substitusikan ke persamaan yang terbentuk di ruas kiri.
1). $ 2x - 1 \geq 3 \rightarrow 2x - 4 \geq 0 $
akar-akarnya : $ 2x - 4 = 0 \rightarrow 2x = 4 \rightarrow x = 2 $
garis bilangannya :
$ x = 0 \rightarrow 2x - 4 = 2.0 - 4 = -4 $
hasilnya negatif, artinya tanda di sebelah kiri 2 negatif($-$)
*). Pilih salah satu angka di sebelah kanan 2, misalkan 4
$ x = 4 \rightarrow 2x - 4 = 2.4 - 4 = 4 $
hasilnya positif, artinya tanda di sebelah kanan 2 positif($+$)
Garis bilangan dan tandanya :
*). Menentukan akar-akar, nolkan ruas kanan.
$ \begin{align} 2x^2 + 2x - 1 & < 1 - x \\ 2x^2 + 2x - 1 + x - 1 & < 0 \\ 2x^2 + 3x - 2 & < 0 \\ (2x-1)(x+2) & = 0 \\ x = \frac{1}{2} \vee x & = -2 \end{align} $
Garis bilangannya
Terbentuk tiga selang/interval, pilih satu angka pada setiap selang dan substitusi ke $ (2x-1)(x+2) $
Interval pertama : $ -\infty < x < -2 \, $ , pilih $ x = -3 $
$ x = - 3 \rightarrow (2x-1)(x+2) = (2.(-3)-1)(-3+2) = -7 . (-1) = 7 \, $ (tanda $+$)
Interval kedua : $ -2 < x < \frac{1}{2} \, $ , pilih $ x = 0 $
$ x = 0 \rightarrow (2x-1)(x+2) = (2.(0)-1)(0+2) = -1 . 2 = -2 \, $ (tanda $-$)
Interval ketiga : $ \frac{1}{2} < x < \infty \, $ , pilih $ x = 1 $
$ x = 1 \rightarrow (2x-1)(x+2) = (2.(1)-1)(1+2) = 1 . 3 = 3 \, $ (tanda $+$)
Garis bilangan dan tandanya :
*). Biasanya tanda pada semua interval selang-seling (misalkan +, - , + , - , atau -, + , - , + )
*). Untuk penjelasan yang lebih mendalam tentang garis bilangan, silahkan baca artikelnya pada "Cara Menentukan Tanda + atau - pada Garis Bilangan"
Langkah-langkah umum menyelesaiakan pertidaksamaan
Langkah - langkah berikut dapat digunakan untuk menyelesaikan semua jenis pertidaksamaan :
$\spadesuit $ Solusi Umum (HP1) :
1). Nolkan ruas kanan
2). Tentukan akar-akar (pembuat nolnya) dari pertidaksamaan dengan cara mengubah ketaksamaan menjadi sama dengan (=) lalu difaktorkan.
3). Tuliskan akar-akar pada garis bilangan dan tentukan tanda setiap intervalnya ( $+$ atau $ - $ setiap daerah)
4). Arsir daerah yang sesuai ( $ > $ untuk $ + $ , dan $ < $ untuk $ - $ )
5). Tulis himpunan penyelesaiannya (HP1)
$ \spadesuit $ Solusi syarat-syarat jika ada ( HP2 ).
*). caranya sama dengan solusi umum di atas
*). solusi syarat biasanya ada pada pertidaksamaan pecahan, bentuk akar, dan logaritma.
$\spadesuit $ Solusi totalnya adalah irisan HP1 dan HP2
$\spadesuit $ Solusi Umum (HP1) :
1). Nolkan ruas kanan
2). Tentukan akar-akar (pembuat nolnya) dari pertidaksamaan dengan cara mengubah ketaksamaan menjadi sama dengan (=) lalu difaktorkan.
3). Tuliskan akar-akar pada garis bilangan dan tentukan tanda setiap intervalnya ( $+$ atau $ - $ setiap daerah)
4). Arsir daerah yang sesuai ( $ > $ untuk $ + $ , dan $ < $ untuk $ - $ )
5). Tulis himpunan penyelesaiannya (HP1)
$ \spadesuit $ Solusi syarat-syarat jika ada ( HP2 ).
*). caranya sama dengan solusi umum di atas
*). solusi syarat biasanya ada pada pertidaksamaan pecahan, bentuk akar, dan logaritma.
$\spadesuit $ Solusi totalnya adalah irisan HP1 dan HP2
Contoh
1). Nilai $ x $ yang memenuhi pertidaksamaan $ 2x - 1 < 7 \, $ adalah ....?
Penyelesaian :
*). Menentukan akar-akarnya
$ 2x - 1 < 7 \rightarrow 2x - 1 = 7 \rightarrow 2x = 8 \rightarrow x = 4 $
*). garis bilangan dan mengarsir daerahnya (diminta $ < $ , arsir negatif)
2). Pertidaksamaan $ ax - 3 > 15 \, $ mempunyai penyelesaian $ x > 6 $.
Nilai $ a \, $ yang memenuhi adalah ....?
Penyelesaian :
Cara I :
$\clubsuit $ Solusi dari pertidaksamaan diperoleh dari akar-akar pertidaksamaan dengan mengubah tanda ketaksamaan menjadi sama dengan.
$ \clubsuit $ Solusinya $ x > 6 \, $ artinya akar-akarnya adalah $ x = 6 $
Substitusi $ x = 6 $ ke persamaan :
$ \begin{align} x = 6 \rightarrow ax - 3 & > 15 \\ a.6 - 3 & = 15 \\ 6a & = 15 + 3 \\ 6a & = 18 \\ a & = 3 \end{align} $
Jadi, nilai $ a = 3 $
Cara II :
$\clubsuit $ Modifikasi pertidaksamaannya
$ ax - 3 > 15 \rightarrow ax > 18 \rightarrow x > \frac{18}{a} $
$\clubsuit $ Solusinya $ x > 6 $
$ \left. \begin{array}{c} x > \frac{18}{a} \\ x > 6 \end{array} \right\} \, $ bentuknya sama
Sehingga $ \frac{18}{a} = 6 \rightarrow a = \frac{18}{6} = 3 $
Jadi, nilai $ a = 3 $
3). Pertidaksamaan $ 3x - a < \frac{5x-2}{3} - \frac{ax-5}{4} \, $ mempunyai penyelesaian $ x < 1 $ .
Tentukan nilai $ a ? $
Penyelesaian :
$ \spadesuit $ Solusinya $ x < 1 \, $ , artinya akarnya adalah $ x = 1 $
$ \spadesuit $ Substitusi $ x = 1 $ ke pertidaksamaan dan ubah ketaksamaannya menjadi sama dengan.
$ \begin{align} x = 1 \rightarrow 3x - a & < \frac{5x-2}{3} - \frac{ax-5}{4} \\ 3.1 - a & = \frac{5.1-2}{3} - \frac{a.1-5}{4} \\ 3 - a & = \frac{3}{3} - \frac{a-5}{4} \\ 3 - a & = 1 - \frac{a-5}{4} \, \, \, \, \text{(kali 4)} \\ 12 - 4a & = 4 - (a-5) \\ 3a & = 3 \\ a & = 1 \end{align} $
Jadi, nilai $ a = 1 $
4). Pertidaksamaan $ ax^2 + bx - 3 \leq 0 \, $ mempunyai penyelesaian $ - \frac{1}{2} \leq x \leq 3 $ .
Tentukan nilai $ a + b ? $
Penyelesaian :
$\clubsuit $ Solusinya $ - \frac{1}{2} \leq x \leq 3 $ , akar-akarnya adalah $ x = - \frac{1}{2} \, $ dan $ x = 3 $
$ \clubsuit $ Substitusi akar-akarnya ke pertidaksamaan :
$ \begin{align} x = - \frac{1}{2} \rightarrow ax^2 + bx - 3 & \leq 0 \\ a(-\frac{1}{2})^2 + b.(-\frac{1}{2}) - 3 & = 0 \\ a(\frac{1}{4}) - b.(\frac{1}{2}) - 3 & = 0 \, \, \, \, \text{(kali 4)} \\ a - 2b - 12 & = 0 \\ a - 2b & = 12 \, \, \, \, \text{...pers(i)} \\ x = 3 \rightarrow ax^2 + bx - 3 & \leq 0 \\ a(3)^2 + b.(3) - 3 & = 0 \\ 9a + 3b & = 3 \, \, \, \, \text{...pers(ii)} \end{align} $
$ \clubsuit $ Eliminasi pers(i) dan pers(ii)
$ \begin{array}{c|c|cc} a - 2b = 12 & \text{kali 3} & 3a - 6b = 36 & \\ 9a + 3b = 3 & \text{kali 2} & 18a + 6b = 6 & + \\ \hline & & 21a = 42 & \\ & & a = 2 & \end{array} $
Pers(i) : $ a - 2b = 12 \rightarrow 2 - 2b = 12 \rightarrow b = -5 $
Sehingga nilai $ a + b = 2 + (-5) = -3 $
Jadi, nilai $ a + b = -3 $
Irisan dan Gabungan dua himpunan
Irisan lambangnya $ \cap \, $ dan gabungan lambangnya $ \cup $
$\clubsuit $ Hasil irisan dua himpunan adalah himpunan nilai yang sama yang terdapat pada kedua himpunan.
$ \clubsuit $ Hasil gabungan dua himpunan adalah himpunan semua nilai yang terdapat pada kedua himpunan.
$\clubsuit $ Hasil irisan dua himpunan adalah himpunan nilai yang sama yang terdapat pada kedua himpunan.
$ \clubsuit $ Hasil gabungan dua himpunan adalah himpunan semua nilai yang terdapat pada kedua himpunan.
Contoh
1). Himpunan $ A = \{1,2,3,4,5,6\} \, $ dan himpunan $ B = \{ 2,3,4,6,7,8\} $
*). Irisannya : $ A \cap B = \{2,3,4\} \, $ (ambil yang sama saja dari kedua himpunan)
*). Gabungannya : $ A \cup B = \{ 1,2,3,4,5,6,7,8\} \, $ (diambil semua, yang sama ditulis satu kali)
2). Diketahui : $ HP1 = \{ -2 < x < 4 \} , \, HP2 = \{ 0 < x < 5 \} $
*). Irisannya : $ HP1 \cap HP2 = \{ 0 < x < 4 \} $
*). Gabungannya : $ HP1 \cup HP2 = \{ -2 < x < 5 \} $
garis bilangannya :
Pertidaksamaan secara umum mempunyai penyelesaian seperti di atas. Artinya apapun jenis pertidaksamaannya, penyelesaiannya sama saja mengikuti langkah-langkah umum di atas. Namun untuk lebih maksimal, silahkan baca artikel pertidaksamaan secara lebih khusus, yaitu pertidaksamaan linear, pertidaksamaan kuadrat, pertidaksamaan pecahan, pertidaksamaan bentuk akar, pertidaksamaan bentuk nilai mutlak.
