Deskripsi dan Definisi Fungsi Komposisi
Jika diketahui $ A = \{a_1, a_2, a_3\}, B = \{b_1, b_2, b_3, b_4\}$, dan $C = \{c1, c2, c3\}$, maka fungsi
$f : A \rightarrow B $ dan $ g : B \rightarrow C $ didefinisikan seperti diagram berikut. 
Definisi Fungsi Komposisi
Diketahui, $f$ dan $g$ dua fungsi sebarang maka fungsi komposisi
$f$ dan $g$ ditulis $g \circ f$, didefinisikan sebagai $(g \circ f)(x) = g(f(x))$ dengan $f$ dikerjakan
lebih dahulu daripada $g$.
Ilustrasi diagram panah untuk fungsi komposisi $ (g \circ f )(x) $ :
Sementara untuk fungsi komposisi
$g$ dan $f$ ditulis $f \circ g$, didefinisikan sebagai $(f \circ g)(x) = f(g(x))$ dengan $g$ dikerjakan
lebih dahulu daripada $f$.
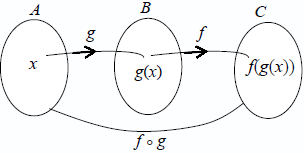
Ilustrasi diagram panah untuk fungsi komposisi $ (f \circ g )(x) $ :
Ilustrasi diagram panah untuk fungsi komposisi $ (g \circ f )(x) $ :
Ilustrasi diagram panah untuk fungsi komposisi $ (f \circ g )(x) $ :
Syarat Fungsi Komposisi
Syarat yang harus dipenuhi agar fungsi $f$ dan fungsi $g$ dapat
dikomposisikan menjadi fungsi komposisi $(g \circ f)$ adalah
irisan antara daerah hasil fungsi $f$ dan daerah asal fungsi
$g$ bukan himpunan kosong, atau $R_f \cap D_g \neq \emptyset $.
Daerah Asal Fungsi Komposisi
*). Misalkan terdefinisi fungsi komposisi $ (g \circ f)(x) \, $ , daerah asalnya ($D_{g \circ f}$) adalah
$ D_{g \circ f} = \{ x | x \in D_f , \, f(x) \in D_g \} $
*). Misalkan terdefinisi fungsi komposisi $ (f \circ g)(x) \, $ , daerah asalnya ($D_{f \circ g}$) adalah $ D_{f \circ g} = \{ x | x \in D_g , \, g(x) \in D_f \} $
Keterangan :
$ D_f = \, $ daerah asal fungsi $ f $
$ D_g = \, $ daerah asal fungsi $ g $
*). Misalkan terdefinisi fungsi komposisi $ (f \circ g)(x) \, $ , daerah asalnya ($D_{f \circ g}$) adalah $ D_{f \circ g} = \{ x | x \in D_g , \, g(x) \in D_f \} $
Keterangan :
$ D_f = \, $ daerah asal fungsi $ f $
$ D_g = \, $ daerah asal fungsi $ g $
Untuk contoh menentukan daerah asal dan daerah hasil fungsi komposisi, silahkan baca artikelnya pada "Daerah asal dan daerah hasil komposisi fungsi".
Contoh:
1). Fungsi $ f $ dan $ g $ dinyatakan dalam himpunan pasangan berurutan berikut.
$ f = \{ (a,b),(c,d),(e,f),(g,h),(i,j)\} $
$ g = \{ (b,-1),(f,a),(h,5), (1,i), (j,c) \} $
Nyatakan fungsi-fungsi komposisi berikut dalam pasangan berurutan.!
a). $ (g \circ f)(x) \, \, \, $ b). $ (f \circ g(x) $
Penyelesaian :
*). Fungsi $ f $ : $ f(a) = b, \, f(c) = d, \, f(e)=f , \, f(g)=h, \, f(i)=j $
Domain fungsi $ f $ : $ D_f = \{ a,c,e,g,i \} $
*). Fungsi $ g $ : $ g(b)=-1, \, g(f)=a, \, g(h)=5, \, g(1)=i, \, g(j)=c $
Domain fungsi $ g $ : $ D_g = \{ b,f,h,1,j \} $
*). Menentukan fungsi komposisinya
a). $ (g \circ f)(x) = g(f(x)) $
Kerjakan fungsi $ f $ dahulu dengan memasukkan domain fungsi $ f $ :
$ x = a \rightarrow (g \circ f)(a) = g(f(a)) = g(b) = -1 , \, $ artinya $ (g \circ f)(a) = -1 $
$ x = c \rightarrow (g \circ f)(c) = g(f(c)) = g(d) = - , \, $ artinya $ (g \circ f)(c) = - $
(tidak ada pasangannya)
$ x = e \rightarrow (g \circ f)(e) = g(f(e)) = g(f) = a , \, $ artinya $ (g \circ f)(e) = a $
$ x = g \rightarrow (g \circ f)(g) = g(f(g)) = g(h) = 5 , \, $ artinya $ (g \circ f)(g) = 5 $
$ x = i \rightarrow (g \circ f)(i) = g(f(i)) = g(j) = c , \, $ artinya $ (g \circ f)(i) = c $
Sehingga diperoleh $ g \circ f = \{(a,-1),(e,a),(g,5),(i,c) \} $
b). $ (f \circ g)(x) = f(g(x)) $
Kerjakan fungsi $ g $ dahulu dengan memasukkan domain fungsi $ g $ :
$ x = b \rightarrow (f \circ g)(a) = f(g(b)) = f(-1) = - , \, $ artinya $ (f \circ g)(b) = - $
(tidak ada pasangannya)
$ x = f \rightarrow (f \circ g)(f) = f(g(f)) = f(a) = b , \, $ artinya $ (f \circ g)(f) = b $
$ x = h \rightarrow (f \circ g)(h) = f(g(h)) = f(5) = - , \, $ artinya $ (f \circ g)(h) = - $
(tidak ada pasangannya)
$ x = 1 \rightarrow (f \circ g)(1) = f(g(1)) = f(i) = j , \, $ artinya $ (f \circ g)(1) = j $
$ x = j \rightarrow (f \circ g)(j) = f(g(j)) = f(c) = d , \, $ artinya $ (f \circ g)(j) = d $
diperoleh $ f \circ g = \{(f,b),(1,j),(j,d) \} $
2). Diketahui fungsi $f: R\rightarrow R $ dengan $ f(x) = x^2 + 2 $ dan fungsi $g: R \rightarrow R $ dengan $ g(x) = \sqrt{1-x} $.
a). Apakah fungsi komposisi $(g \circ f )(x)$ dan $(f \circ g)(x)$ terdefinisi?
b). Tentukan fungsi komposisi $(g \circ f )(x)$ dan $(f \circ g)(x)$ !
Penyelesaian :
*). Menentukan Domain dan Range fungsi $ f $ dan fungsi $ g $ :
Fungsi $ f(x) = x^2 + 2 \rightarrow D_f = \{x | x \in R \} \, $ dan $ R_f = \{y|y \geq 2 \} $
Fungsi $ g(x) = \sqrt{1-x} \rightarrow D_g = \{x | x \leq 1 \} \, $ dan $ R_g = \{y|y \geq 0 \} $
a). Untuk menentukan apakah fungsi komposisi $(g \circ f )(x)$ dan $(f \circ g)(x)$ terdefinisi, diketahui berdasarkan:
*). Jika $R_f \cap D_g \neq \emptyset $ maka $(g \circ f)(x)$ terdefinisi.
$ R_f \cap D_g = \{y|y \geq 2 \} \cap \{x | x \leq 1 \} = \emptyset $
Karena $R_f \cap D_g = \emptyset $ maka $(g \circ f)(x)$ tidak terdefinisi, artinya fungsi komposisi $(g \circ f)(x)$ tidak bisa dicari hasilnya.
*). Jika $R_g \cap D_f \neq \emptyset $ maka $(f \circ g)(x)$ terdefinisi.
$ R_g \cap D_f = \{y|y \geq 0 \} \cap \{x | x \in R \} = \{x | x \geq 0, \, x \in R \} \neq \emptyset $
Karena $R_g \cap D_f \neq \emptyset $ maka $(f \circ g)(x)$ terdefinisi, artinya fungsi komposisi $(f \circ g)(x)$ bisa dicari hasilnya.
b). Menentukan fungsi komposisi $(g \circ f )(x)$ dan $(f \circ g)(x)$
*). Menentukan $ (g \circ f )(x)$
$\begin{align} (g \circ f )(x) & = g(f(x)) \\ & = g(x^2 + 2) \\ & = \sqrt{1-(x^2 + 2)} \\ & = \sqrt{-(x^2+1)} \end{align} $
Karena hasilnya adalah bilangan real (R), maka bentuk $ (g \circ f )(x) = \sqrt{-(x^2+1)} \, $ tidak terdefinisi (dalam akar selalu negatif, padahal pada bilangan real tidak ada akar negatif). Ini artinya fungsi komposisi $ (g \circ f )(x) \, $ tidak ada hasilnya, dan ini sesuai dengan pernyataan a) di atas yaitu bentuk $ (g \circ f )(x) \, $ tidak terdefinisi.
*). Menentukan $ (f \circ g )(x)$
$\begin{align} (f \circ g )(x) & = f(g(x)) \\ & = f(\sqrt{1-x} ) \\ & = (\sqrt{1-x} )^2 + 2 \\ & = (1-x) + 2 \\ & = 3-x \end{align} $
Sehingga diperoleh, $ (f \circ g )(x) = 3-x $
3). Diketahui fungsi $ f(x) = 5x^2 - 3 \, $ dan $ g(x) = 2x + 1 $, tentukan nilai $ (f \circ g)(-1) $ ?
Penyelesaian :
Ada dua cara menyelesaikan soal yaitu dengan mencari fungsi komposisinya atau dengan langsung menghitung nilai komposisinya.
*). Cara I : menentukan fungsi komposisinya
$ \begin{align} (f \circ g)(x) & = f(g(x)) \\ & = f(2x+1) \\ & = 5(2x+1)^2 - 3 \\ & = 5(4x^2 + 4x + 1) - 3 \\ & = 20x^2 + 20x + 5 - 3 \\ (f \circ g)(x) & = 20x^2 + 20x + 2 \end{align} $
Sehingga nilai $ (f \circ g)(-1) $
$ \begin{align} (f \circ g)(x) & = 20x^2 + 20x + 2 \\ (f \circ g)(-1) & = 20(-1)^2 + 20(-1) + 2 \\ & = 20.1 -20 + 2 \\ & = 2 \end{align} $
*). Cara II : Langsung substitusi nilai $ x = -1 $
$\begin{align} (f \circ g)(-1) & = f(g(-1)) \\ & = f(2.(-1) + 1) \\ & = f(-1) \\ & = 5(-1)^2 - 3 \\ & = 5 - 3 \\ & = 2 \end{align} $
Jadi, nilai $ (f \circ g)(-1) = 2 $ .
4). Diketahui fungsi $ f(x) = 3x -1 $ dan $ g(x) = 2 - x $. Jika $ (f \circ g)(a) = -1 $ , maka nilai $ a^2 + 2 = .... $
Penyelesaian :
Disini kita tidak perlu mencari bentuk komposisinya dulu, tapi langsung kita substitusi nilai $ x = a $ untuk menentukan nilai $ a $ .
$\begin{align} (f \circ g)(a) & = -1 \\ f(g(a)) & = -1 \\ f(2-a) & = -1 \\ 3(2-a) - 1 & = -1 \\ 6 - 3a - 1 & = -1 \\ 5 - 3a & = -1 \\ 3a & = 6 \\ a & = 2 \end{align} $
sehingga nilai $ a^2 + 2 = 2^2 + 2 = 4 + 2 = 6 $
Sifat-sifat operasi fungsi komposisi
Bila $f, g$, dan $h$ suatu fungsi, maka:
a. tidak berlaku sifat komutatif, yaitu $(f \circ g)(x) \neq (g \circ f)(x)$;
b. jika $I$ fungsi identitas ($I(x) = x$) berlaku :
$(I \circ f)(x) = (f \circ I)(x) = f(x)$;
c. berlaku sifat asosiatif, yaitu : $(f \circ (g \circ h))(x) = ((f \circ g) \circ h)(x)$.
a. tidak berlaku sifat komutatif, yaitu $(f \circ g)(x) \neq (g \circ f)(x)$;
b. jika $I$ fungsi identitas ($I(x) = x$) berlaku :
$(I \circ f)(x) = (f \circ I)(x) = f(x)$;
c. berlaku sifat asosiatif, yaitu : $(f \circ (g \circ h))(x) = ((f \circ g) \circ h)(x)$.
contoh :
1). Diketahui $f(x) = 2x - 5, g(x) = x^2 +x - 3$.
a. Tentukan $(g \circ f)(x)$.
b. Tentukan $(f \circ g)(x)$. c. Apakah berlaku sifat komutatif: $g \circ f = f \circ g$?
Penyelesaian :
$\begin{align} \text{a. } \, (g\circ f)(x) & = g(f(x)) \\ & = g(2x - 5) \\ & = (2x - 5)^2 + (2x - 5) - 3 \\ & = (4x^2 -20x + 25 ) + (2x - 5) - 3 \\ & = (4x^2 -20x + 25 ) + (2x - 5) - 3 \\ & = 4x^2 - 18x + 17 \\ \\ \text{b. } \, (f \circ g)(x) & = f(g(x)) \\ & = f(x^2 +x - 3) \\ & = 2(x^2 +x - 3) - 5 \\ & = 2x^2 + 2x - 6 - 5 \\ & = 2x^2 + 2x - 11 \end{align} $
c. Tidak berlaku sifat komutatif karena $ (g\circ f)(x) \neq (f \circ g)(x) $ .
2). Diketahui $f(x) = 3x - 7 $ dan $I(x) = x$.
Buktikan $I \circ f = f \circ I = f. $
Pembuktian :
$ \begin{align} (I \circ f)(c) & = I(f(x)) \\ & = I(3x - 7) \\ & = 3x - 7 \\ \\ (f \circ I)(x) & = f(I(x)) \\ & = f(x) \\ & = 3x - 7 \end{align} $
Tampak bahwa $I \circ f = f \circ I = f $ (terbukti).
3). Diketahui $f(x) = x^2, \, g(x) = x + 2$, dan $h(x) = 3x$.
a. Tentukan $(f \circ (g \circ h))(x)$.
b. Tentukan $((f \circ g) \circ h)(x)$.
c. Apakah $f \circ (g \circ h) = (f \circ g) \circ h$ , mengapa?
Penyelesaian :
a. $ (f \circ (g \circ h))(x) = ... $
$ \begin{align} \text{Misalkan } \, p(x) & = (g \circ h)(x) \\ & = g(h(x)) \\ & = g(3x) \\ & = 3x + 2 \end{align} $
Soalnya menjadi :
$ \begin{align} (f \circ (g \circ h))(x) & = (f \circ (g \circ h)(x)) \\ & = (f \circ p)(x) \\ & = f(p(x)) \\ & = f(3x + 2) \\ & = (3x+2)^2 \\ & = 9x^2 + 12x + 4 \end{align} $
b. $ ((f \circ g) \circ h)(x) = ... $
$ \begin{align} \text{Misalkan } \, q(x) & = (f \circ g)(x) \\ & = f(g(x)) \\ & = f(x+2) \\ & = (x+2)^2 \\ & = x^2 + 4x + 4 \end{align} $
Soalnya menjadi :
$ \begin{align} ((f \circ g) \circ h)(x) & = (q \circ h)(x) \\ & = q(h(x)) \\ & = q(3x) \\ & = (3x)^2 + 4(3x) + 4 \\ & = 9x^2 + 12x + 4 \end{align} $
c. Ya, benar berlaku $f \circ (g \circ h) = (f \circ g) \circ h$ , karena bersifat asosiatif.
Menentukan komponen pembentuk fungsi komposisi
Menentukan fungsi $ f $ atau fungsi $ g $ dari fungsi komposisinya
Jika diketahui fungsi komposisinya $ (g \circ f)(x) \, $ atau $ (f \circ g)(x) \, $ dan diketaui salah satu fungsinya bisa
fungsi $ f $ atau fungsi $ g $, maka kita diminta menentukan fungsi yang belum diketahui.
Cara Umumnya :
*). yang ditanyakan bagian kanan
Misal diketahui fungsi $ f $ dan fungsi komposisi $ (f \circ g)(x) $ , kita diminta menentukan fungsi $ g $. Caranya, langsung substitusi bentuk $ g(x) $ ke fungsi $ f $, maksudnya semua variabel $ x $ pada fungsi $ f $ digantikan dengan $ g(x) $.
*). yang ditanyakan bagian kiri
Misal diketahui fungsi $ f $ dan fungsi komposisi $ (g \circ f)(x) $ , kita diminta menentukan fungsi $ g $. Caranya, substitusi bentuk fungsi $ f(x) $ ke komposisinya, lalu misalkan agar menjadi satu variabel.
Cara Umumnya :
*). yang ditanyakan bagian kanan
Misal diketahui fungsi $ f $ dan fungsi komposisi $ (f \circ g)(x) $ , kita diminta menentukan fungsi $ g $. Caranya, langsung substitusi bentuk $ g(x) $ ke fungsi $ f $, maksudnya semua variabel $ x $ pada fungsi $ f $ digantikan dengan $ g(x) $.
*). yang ditanyakan bagian kiri
Misal diketahui fungsi $ f $ dan fungsi komposisi $ (g \circ f)(x) $ , kita diminta menentukan fungsi $ g $. Caranya, substitusi bentuk fungsi $ f(x) $ ke komposisinya, lalu misalkan agar menjadi satu variabel.
1). Diketahui fungsi $ f(x) = 2x - 3 \, $ dan $ (f \circ g)(x) = 4x^2 - 6x + 5 $. Tentukan fungsi $ g(x) $!
Penyelesaian :
$ \begin{align} (f \circ g)(x) & = 4x^2 - 6x + 5 \\ f(g(x)) & = 4x^2 - 6x + 5 \\ 2[g(x)] - 3 & = 4x^2 - 6x + 5 \\ 2[g(x)] & = 4x^2 - 6x + 5 + 3 \\ 2[g(x)] & = 4x^2 - 6x + 8 \\ g(x) & = \frac{4x^2 - 6x + 8}{2} \\ g(x) & = 2x^2 - 3x + 4 \end{align} $
Jadi, diperoleh fungsi $ g(x) = 2x^2 - 3x + 4 $
2). Diketahui fungsi $ g(x) = 3x + 2 \, $ dan $ (f \circ g)(x) = x^2 +x - 3 $. Tentukan fungsi $ f(x) $ nya !
Penyelesaian :
$ \begin{align} (f \circ g)(x) & = x^2 +x - 3 \\ f(g(x)) & = x^2 +x - 3 \\ f(3x+2) & = x^2 +x - 3 \\ \text{misal } p & = 3x+2 \rightarrow x = \frac{p-2}{3} \\ \text{substitusikan } p & = 3x+2 \\ f(3x+2) & = x^2 +x - 3 \\ f(p) & = \left( \frac{p-2}{3} \right)^2 + \left( \frac{p-2}{3} \right) - 3 \\ f(p) & = \frac{p^2-4p + 4}{9} + \frac{p-2}{3} - 3 \\ f(p) & = \frac{p^2-4p + 4}{9} + \frac{3(p-2)}{9} - \frac{27}{9} \\ f(p) & = \frac{p^2-4p + 4}{9} + \frac{3p-6}{9} - \frac{27}{9} \\ f(p) & = \frac{(p^2-4p + 4) + (3p-6) + 27 }{9} \\ f(p) & = \frac{p^2 - p + 25 }{9} \end{align} $
Sehingga diperoleh : $ f(p) = \frac{p^2 - p + 25 }{9} \rightarrow f(x) = \frac{x^2 - x + 25 }{9} $
Jadi, diperoleh fungsi $ f(x) = \frac{x^2 - x + 25 }{9} $
